双周赛118（模拟、分组循环、记忆化搜索==＞动态规划、单调队列优化DP）

文章目录

双周赛118
- [100121. 查找包含给定字符的单词](https://leetcode.cn/problems/find-words-containing-character/)
- - 模拟
- [100138. 最大化网格图中正方形空洞的面积](https://leetcode.cn/problems/maximize-area-of-square-hole-in-grid/)
- - 题意转换 + 分组循环
- [100133. 购买水果需要的最少金币数](https://leetcode.cn/problems/minimum-number-of-coins-for-fruits/)
- - 记忆化搜索（枚举买还是不买）
  - 记忆化搜索（枚举买哪个）==>动态规划(更优雅的解法)
  - 单调队列优化DP
- [100135. 找到最大非递减数组的长度](https://leetcode.cn/problems/find-maximum-non-decreasing-array-length/)
- - 单调队列优化DP

双周赛118

100121. 查找包含给定字符的单词

简单

给你一个下标从 0 开始的字符串数组 words 和一个字符 x 。

请你返回一个 下标数组 ，表示下标在数组中对应的单词包含字符 x 。

注意，返回的数组可以是任意顺序。

示例 1：

输入：words = ["leet","code"], x = "e"
输出：[0,1]
解释："e" 在两个单词中都出现了："leet" 和 "code" 。所以我们返回下标 0 和 1 。

示例 2：

输入：words = ["abc","bcd","aaaa","cbc"], x = "a"
输出：[0,2]
解释："a" 在 "abc" 和 "aaaa" 中出现了，所以我们返回下标 0 和 2 。

示例 3：

输入：words = ["abc","bcd","aaaa","cbc"], x = "z"
输出：[]
解释："z" 没有在任何单词中出现。所以我们返回空数组。

提示：

1 <= words.length <= 50
1 <= words[i].length <= 50
x 是一个小写英文字母。
words[i] 只包含小写英文字母。

模拟

class Solution {
    public List<Integer> findWordsContaining(String[] words, char x) {
        List<Integer> res = new ArrayList<>();
        for(int i = 0; i < words.length; i++){
            if(words[i].indexOf(x) != -1)
                res.add(i);
        }
        return res;
    }
}

100138. 最大化网格图中正方形空洞的面积

中等

给你一个网格图，由 n + 2 条 横线段 和 m + 2 条 竖线段 组成，一开始所有区域均为 1 x 1 的单元格。

所有线段的编号从 1 开始。

给你两个整数 n 和 m 。

同时给你两个整数数组 hBars 和 vBars 。

hBars 包含区间 [2, n + 1] 内 互不相同 的横线段编号。
vBars 包含 [2, m + 1] 内 互不相同的 竖线段编号。

如果满足以下条件之一，你可以移除两个数组中的部分线段：

如果移除的是横线段，它必须是 hBars 中的值。
如果移除的是竖线段，它必须是 vBars 中的值。

请你返回移除一些线段后（可能不移除任何线段），剩余网格图中 最大正方形 空洞的面积，正方形空洞的意思是正方形内部不含有任何线段。

示例 1：

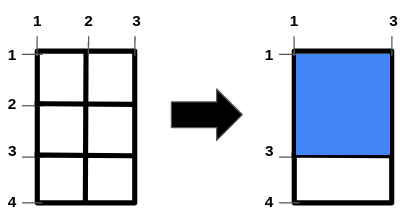
输入：n = 2, m = 1, hBars = [2,3], vBars = [2]
输出：4
解释：左边的图是一开始的网格图。
横线编号的范围是区间 [1,4] ，竖线编号的范围是区间 [1,3] 。
可以移除的横线段为 [2,3] ，竖线段为 [2] 。
一种得到最大正方形面积的方法是移除横线段 2 和竖线段 2 。
操作后得到的网格图如右图所示。
正方形空洞面积为 4。
无法得到面积大于 4 的正方形空洞。
所以答案为 4 。

示例 2：

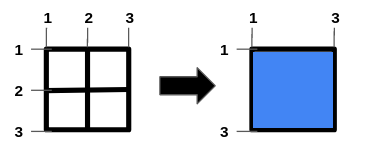
输入：n = 1, m = 1, hBars = [2], vBars = [2]
输出：4
解释：左边的图是一开始的网格图。
横线编号的范围是区间 [1,3] ，竖线编号的范围是区间 [1,3] 。
可以移除的横线段为 [2] ，竖线段为 [2] 。
一种得到最大正方形面积的方法是移除横线段 2 和竖线段 2 。
操作后得到的网格图如右图所示。
正方形空洞面积为 4。
无法得到面积大于 4 的正方形空洞。
所以答案为 4 。

示例 3：

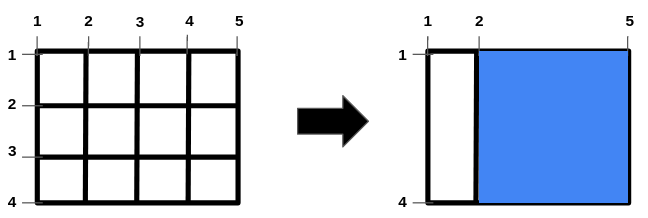
输入：n = 2, m = 3, hBars = [2,3], vBars = [2,3,4]
输出：9
解释：左边的图是一开始的网格图。
横线编号的范围是区间 [1,4] ，竖线编号的范围是区间 [1,5] 。
可以移除的横线段为 [2,3] ，竖线段为 [2,3,4] 。
一种得到最大正方形面积的方法是移除横线段 2、3 和竖线段 3、4 。
操作后得到的网格图如右图所示。
正方形空洞面积为 9。
无法得到面积大于 9 的正方形空洞。
所以答案为 9 。

提示：

1 <= n <= 109
1 <= m <= 109
1 <= hBars.length <= 100
2 <= hBars[i] <= n + 1
1 <= vBars.length <= 100
2 <= vBars[i] <= m + 1
hBars 中的值互不相同。
vBars 中的值互不相同。

题意转换 + 分组循环

https://leetcode.cn/problems/maximize-area-of-square-hole-in-grid/solutions/2542812/heng-shu-fen-bie-tong-ji-fen-zu-xun-huan-nboj/

class Solution {
    /**
    考虑最大矩形面积，再考虑正方形的面积
        矩形面积是长和宽的乘积
    横线竖线相互独立，以hBars为例
        如果不做任何移除，那么最长长度为 1。
        如果移除一条线，那么最长长度为 2。
        如果移除两条编号相邻的线，那么最长长度为 3。
        如果移除三条编号连续的线，那么最长长度为 4。
        依此类推。
    把hBars排序，找连续递增最长字段，子段+1就是这条边的最长长度
    求出后，正方形的边长是长宽的最小值
     */
    public int maximizeSquareHoleArea(int n, int m, int[] hBars, int[] vBars) {
        int size = Math.min(f(hBars), f(vBars));
        return size * size;
    }

    // 找连续递增最长字段
    public int f(int[] nums){
        Arrays.sort(nums);
        int ans = 0, i = 0;
        int n = nums.length;
        while(i < n){
            int start = i;
            i += 1;
            while(i < n && nums[i] - nums[i-1] == 1)
                i++;
            ans = Math.max(ans, i - start);
        }
        return ans + 1;
    }
}

100133. 购买水果需要的最少金币数

中等

你在一个水果超市里，货架上摆满了玲琅满目的奇珍异果。

给你一个下标从 1 开始的数组 prices ，其中 prices[i] 表示你购买第 i 个水果需要花费的金币数目。

水果超市有如下促销活动：

如果你花费 price[i] 购买了水果 i ，那么接下来的 i 个水果你都可以免费获得。

注意，即使你可以免费获得水果 j ，你仍然可以花费 prices[j] 个金币去购买它以便能免费获得接下来的 j 个水果。

请你返回获得所有水果所需要的最少金币数。

示例 1：

输入：prices = [3,1,2]
输出：4
解释：你可以按如下方法获得所有水果：
- 花 3 个金币购买水果 1 ，然后免费获得水果 2 。
- 花 1 个金币购买水果 2 ，然后免费获得水果 3 。
- 免费获得水果 3 。
注意，虽然你可以免费获得水果 2 ，但你还是花 1 个金币去购买它，因为这样的总花费最少。
购买所有水果需要最少花费 4 个金币。

示例 2：

输入：prices = [1,10,1,1]
输出：2
解释：你可以按如下方法获得所有水果：
- 花 1 个金币购买水果 1 ，然后免费获得水果 2 。
- 免费获得水果 2 。
- 花 1 个金币购买水果 3 ，然后免费获得水果 4 。
- 免费获得水果 4 。
购买所有水果需要最少花费 2 个金币。

提示：

1 <= prices.length <= 1000
1 <= prices[i] <= 105

记忆化搜索（枚举买还是不买）

class Solution {
    int[] prices;
    int[][] cache;
    public int minimumCoins(int[] prices) {
        this.prices = prices;
        int n = prices.length;
        cache = new int[n][2100];
        for(int i = 0; i < n; i++)
            Arrays.fill(cache[i], -1);
        return dfs(0, 0);
    }

    /**
    定义 dfs(i, free) 表示当前购买到i，能免费购买的水果编号<free，所需要的最少金币数
     */
    public int dfs(int i, int free){
        if(i == prices.length)
            return 0;
        if(cache[i][free] >= 0) return cache[i][free];
        int res = Integer.MAX_VALUE / 2;
        // 买
        res = Math.min(res, dfs(i+1, i + i + 1 + 1) + prices[i]);
        // 不买
        if(free > i)
            res = Math.min(res, dfs(i+1, free));
        return cache[i][free] = res;
    }
}

记忆化搜索（枚举买哪个）==>动态规划(更优雅的解法)

https://leetcode.cn/problems/minimum-number-of-coins-for-fruits/solutions/2542044/dpcong-on2-dao-onpythonjavacgo-by-endles-nux5/

class Solution {
    int[] prices;
    int[] cache;
    public int minimumCoins(int[] prices) {
        int n = prices.length;
        this.prices = prices;
        cache = new int[n];
        Arrays.fill(cache, -1);
        return dfs(1);
    }

    /**
    定义 dfs(i) 表示获得第i个以及后面的水果所需要的最少金币数，i从1开始
    转移 
        枚举下一个需要购买的水果j,范围 [i+1, 2i+1]
    所有情况取最小值 即 dfs(i) = prices[i] + min(dfs(j))  j [i+1, 2i+1]
    递归边界： dfs(i) = prices[i], 2i>=n 「2i>n时，后面的水果都可以免费获得」
    递归入口：dfs(1)
     */
    public int dfs(int i){
        if(i * 2 >= prices.length)
            return prices[i-1];
        if(cache[i] >= 0)
            return cache[i];
        int res = Integer.MAX_VALUE;
        for(int j = i + 1; j <= i * 2 + 1; j++)
            res = Math.min(res, dfs(j));
        return cache[i] = res + prices[i-1];
    }
}

转递推

class Solution {
    public int minimumCoins(int[] prices) {
        int n = prices.length;
        for(int i = (n+1)/2-1; i > 0; i--){
            int mn = Integer.MAX_VALUE;
            for(int j = i; j <= i*2; j++)
                mn = Math.min(mn, prices[j]);
            prices[i-1] += mn;
        }
        return prices[0];
    }
}

单调队列优化DP

class Solution {
    /**
    j [i+1, 2i+1]
    注意到随着i变小，j的范围也在变小，计算min(dfs(j))的过程类似求滑动窗口最小值
    
    单调队列（单增）的原则 左边的小淘汰掉右边的大
     */
    public int minimumCoins(int[] prices) {
        int n = prices.length;
        Deque<int[]> dq = new ArrayDeque<>();
        dq.addLast(new int[]{n+1, 0}); // 哨兵 [下标，f[i]]
        // 队首在左边，队尾在右边
        for(int i = n; i > 0; i--){
            // 弹出离开窗口的元素
            while(dq.peekLast()[0] > i * 2 + 1){ // 右边离开窗口
                dq.pollLast();
            }
            // 每次转移只需要取队尾的数，它一定是最小的数
            int f = prices[i-1] + dq.peekLast()[1];
			
            while(f <= dq.peekFirst()[1]){
                dq.pollFirst();
            }
            dq.addFirst(new int[]{i, f}); // 左边进入窗口
        }
        return dq.peekFirst()[1];
    }
}

100135. 找到最大非递减数组的长度

困难

给你一个下标从 0 开始的整数数组 nums 。

你可以执行任意次操作。每次操作中，你需要选择一个 子数组 ，并将这个子数组用它所包含元素的和替换。比方说，给定数组是 [1,3,5,6] ，你可以选择子数组 [3,5] ，用子数组的和 8 替换掉子数组，然后数组会变为 [1,8,6] 。

请你返回执行任意次操作以后，可以得到的 最长非递减 数组的长度。

子数组 指的是一个数组中一段连续非空的元素序列。

示例 1：

输入：nums = [5,2,2]
输出：1
解释：这个长度为 3 的数组不是非递减的。
我们有 2 种方案使数组长度为 2 。
第一种，选择子数组 [2,2] ，对数组执行操作后得到 [5,4] 。
第二种，选择子数组 [5,2] ，对数组执行操作后得到 [7,2] 。
这两种方案中，数组最后都不是 非递减 的，所以不是可行的答案。
如果我们选择子数组 [5,2,2] ，并将它替换为 [9] ，数组变成非递减的。
所以答案为 1 。

示例 2：

输入：nums = [1,2,3,4]
输出：4
解释：数组已经是非递减的。所以答案为 4 。

示例 3：

输入：nums = [4,3,2,6]
输出：3
解释：将 [3,2] 替换为 [5] ，得到数组 [4,5,6] ，它是非递减的。
最大可能的答案为 3 。

提示：

1 <= nums.length <= 105
1 <= nums[i] <= 105

单调队列优化DP

单调队列需要思考清楚三步

转移之前，去掉队首无用数据
计算转移
去掉队尾无用数据

class Solution {
    /**
    划分型DP
    DFS最后一段从 i 到 n-1
    定义 f(i) 表示操作下标 0~i 的最长长度
        last[i] 表示这个操作后，最后一个数字的大小
        在f[i]尽量大的前提下，last[i]越小越好
        s[]前缀和 s[i]-s[j]表示从 j+1 到 i 的元素和
         6 5  1 9
    f    1 1  2 3
    last 6 11 6 9

    f[i] = (f[j]+1 , 把j+1到i的这一段合并成一个数
    s[i]-s[j] >= last[j] =>  s[i] >= last[j] + s[j]
    如何找到关系？

    考虑两个转移来源j和k，如果j < k且s[j]+last[j] >= s[k]+last[k]  
        这意味着如果能从f[j]转移到f[i],那么也一定能从f[k]转移到f[i]
        又由于f[j]<=f[k],所以永远不需要从f[j]转移到f[i]
    所以可以用单调队列来维护j,满足从队首到队尾的j和s[j]+last[j]都是严格递增的

    单调队列需要思考清楚三步
    1. 转移之前，去掉队首无用数据
        由于i越大s[i]越大,满足s[j]+last[j]<=s[i]的j也越大,转移来源f[j]也越大
    2. 计算转移
        从单调队列中找到最大的j，满足s[j]+last[j]<=s[i]
            ==>f[i] = f[j]+1和last[i] = s[i]-s[j]
    3. 去掉队尾无用数据
        把i加入队尾，在此之前弹出s[j]+last[j] >= s[i]+last[i] 的j
     */
    public int findMaximumLength(int[] nums) {
        int n = nums.length;
        long[] s = new long[n + 1];
        int[] f = new int[n + 1];
        long[] last = new long[n + 1];
        int[] q = new int[n + 1]; // 数组模拟队列
        int front = 0, rear = 0;
        for (int i = 1; i <= n; i++) {
            s[i] = s[i - 1] + nums[i - 1];
            
            // 1. 去掉队首无用数据（计算转移时，直接取队首）
            while (front < rear && s[q[front + 1]] + last[q[front + 1]] <= s[i]) {
                front++;
            }
            
            // 2. 计算转移
            f[i] = f[q[front]] + 1; 
            last[i] = s[i] - s[q[front]];
            
            // 3. 去掉队尾无用数据
            while (rear >= front && s[q[rear]] + last[q[rear]] >= s[i] + last[i]) {
                rear--;
            }
            q[++rear] = i;
        }
        return f[n];
    }
}