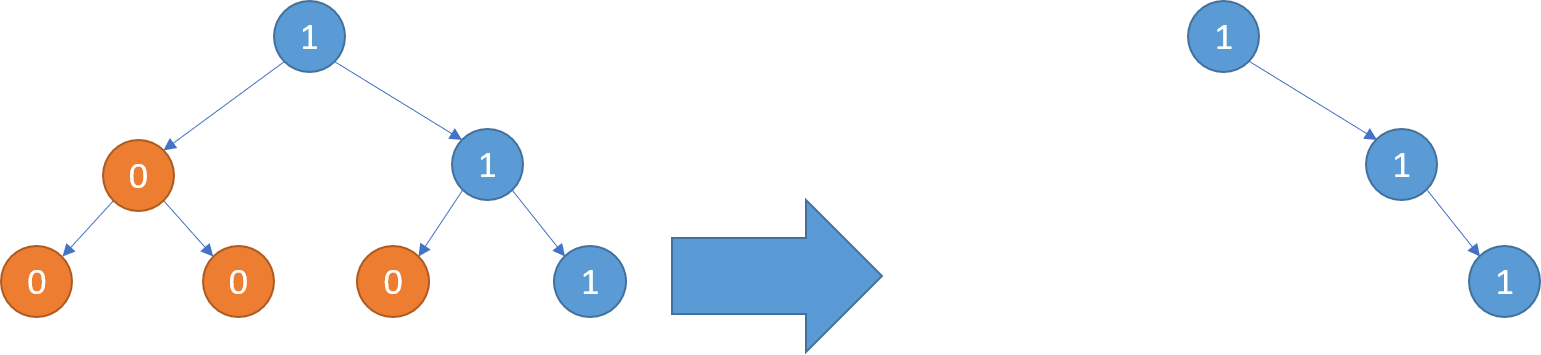
给定一个二叉树 根节点 root ,树的每个节点的值要么是 0,要么是 1。请剪除该二叉树中所有节点的值为 0 的子树。节点 node 的子树为 node 本身,以及所有 node 的后代。
示例 1:
输入: [1,null,0,0,1] 输出: [1,null,0,null,1] 解释: 只有红色节点满足条件“所有不包含 1 的子树”。 右图为返回的答案。

示例 2:
输入: [1,0,1,0,0,0,1] 输出: [1,null,1,null,1] 解释:
示例 3:
输入: [1,1,0,1,1,0,1,0] 输出: [1,1,0,1,1,null,1] 解释:

(1)解法一:
class Solution {
public:
bool dfs(TreeNode* node) {
if(node==nullptr) return false;
bool left = dfs(node->left);
bool right = dfs(node->right);
// 叶子节点且值为0 执行删除
if(left==false && right==false && node->val == 0) return false;
// 非叶子节点左孩子返回false,将其删除,具体操作为node->left = nullptr
if(left==false) node->left = nullptr;
// 非叶子节点右孩子返回false,将其删除,具体操作为node->right = nullptr
if(right==false) node->right = nullptr;
return true;
}
TreeNode* pruneTree(TreeNode* root) {
return dfs(root)?root:nullptr;
}
};(2)解法二:
class Solution {
public:
int dfs(TreeNode* node) {
if(node==nullptr) return 0;
int left = dfs(node->left);
int right = dfs(node->right);
if(left==0) node->left=nullptr;
if(right==0) node->right=nullptr;
return left+right+node->val;
}
TreeNode* pruneTree(TreeNode* root) {
int ans = dfs(root);
if(ans==0) return nullptr;
return root;
}
};(3)解法三:
class Solution {
public:
TreeNode* pruneTree(TreeNode* root) {
if(root == nullptr) return nullptr;
root->left = pruneTree(root->left);
root->right = pruneTree(root->right);
if(root->left==nullptr && root->right==nullptr && root->val == 0) { // 如果叶子节点的值为0就删除该节点
return nullptr;
}
return root;
}
};leetCode 1110. 删点成林 1110. 删点成林 - 力扣(LeetCode)
给出二叉树的根节点 root,树上每个节点都有一个不同的值。如果节点值在 to_delete 中出现,我们就把该节点从树上删去,最后得到一个森林(一些不相交的树构成的集合)。返回森林中的每棵树。你可以按任意顺序组织答案。
示例 1:
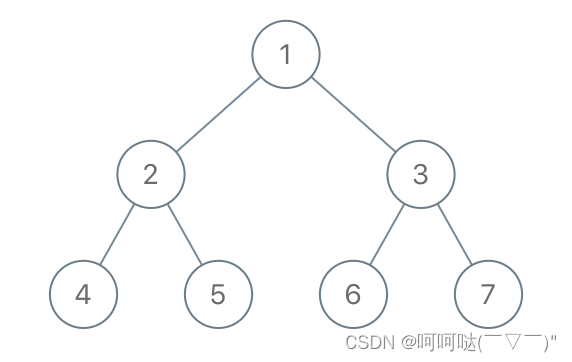
输入:root = [1,2,3,4,5,6,7], to_delete = [3,5] 输出:[[1,2,null,4],[6],[7]]
示例 2:
输入:root = [1,2,4,null,3], to_delete = [3] 输出:[[1,2,4]]
解法一:
class Solution {
public:
vector<TreeNode *> ans;
unordered_set<int> delSet;
bool dfs(TreeNode *node) {
if(node==nullptr) return false;
bool left = dfs(node->left);
bool right = dfs(node->right);
if(delSet.count(node->val)) {
if(left) ans.push_back(node->left);
if(right) ans.push_back(node->right);
return false;
}
if(left==false) node->left = nullptr;
if(right==false) node->right = nullptr;
return node;
}
vector<TreeNode *> delNodes(TreeNode *root, vector<int> &to_delete) {
for(const auto &a:to_delete) {
delSet.insert(a);
}
if (dfs(root)) ans.push_back(root);
return ans;
}
};解法二:
class Solution {
public:
vector<TreeNode *> ans;
unordered_set<int> delSet;
TreeNode * dfs(TreeNode *node) {
if(node==nullptr) return nullptr;
node->left = dfs(node->left);
node->right = dfs(node->right);
if(delSet.count(node->val)) {
if(node->left) ans.push_back(node->left);
if(node->right) ans.push_back(node->right);
return nullptr; // 相当于删除节点
}
return node;// 没有删除
}
vector<TreeNode *> delNodes(TreeNode *root, vector<int> &to_delete) {
for(const auto &a:to_delete) {
delSet.insert(a);
}
if (dfs(root)) ans.push_back(root);
return ans;
}
};解法三(来自灵茶山艾府的题解),和解法二思路差不多:
class Solution {
vector<TreeNode *> ans;
unordered_set<int> s;
TreeNode *dfs(TreeNode *node) {
if (node == nullptr) return nullptr;
node->left = dfs(node->left);
node->right = dfs(node->right);
if (!s.count(node->val)) return node;
if (node->left) ans.push_back(node->left);
if (node->right) ans.push_back(node->right);
return nullptr;
}
public:
vector<TreeNode *> delNodes(TreeNode *root, vector<int> &to_delete) {
for (int x: to_delete) s.insert(x);
if (dfs(root)) ans.push_back(root);
return ans;
}
};未完待续~