目录
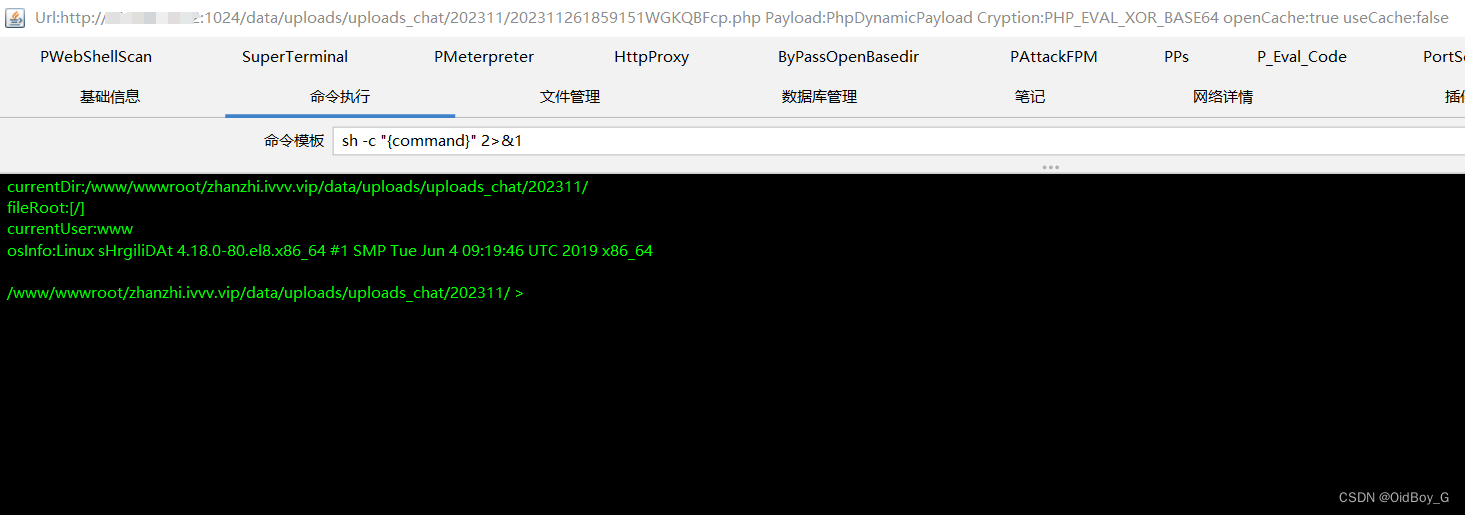
习题5-2 证明宽卷积具有交换性, 即公式(5.13).
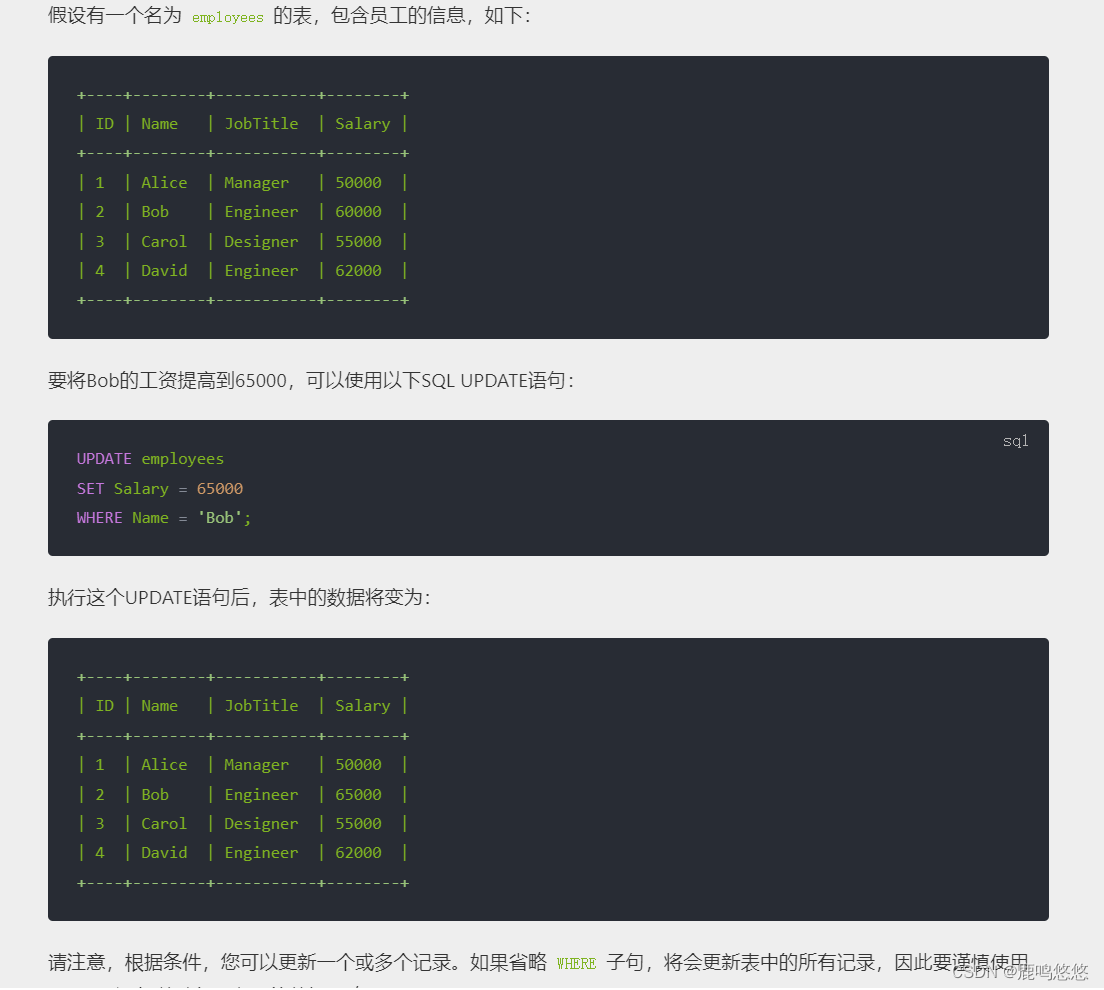
习题5-4 对于一个输入为100 × 100 × 256的特征映射组, 使用3 × 3的卷积核, 输出为100 × 100 × 256的特征映射组的卷积层, 求其时间和空间复杂度. 如果引入一个1 × 1卷积核, 先得到100 × 100 × 64的特征映射, 再进行3 × 3的卷积, 得到100 × 100 × 256的特征映射组, 求其时间和空间复杂度.
习题5-5 对于一个二维卷积, 输入为3 × 3, 卷积核大小为2 × 2, 试将卷积操作重写为仿射变换的形式. 参见公式(5.45) .
编辑
习题5-7 忽略激活函数,分析卷积网络中卷积层的前向计算和反向传播是一种转置关系
习题5-8 在空洞卷积中, 当卷积核大小为𝐾, 膨胀率为𝐷时, 如何设置零填充𝑃的值以使得卷积为等宽卷积 .
习题5-2 证明宽卷积具有交换性, 即公式(5.13).
给定图像![]() 和卷积核
和卷积核![]() 对图像X进行零填充,两端各补
对图像X进行零填充,两端各补 和
个零,得到全填充图像
![]()
图像X和卷积核W的宽卷积定义为
![]()
图像X和卷积核W有固定长度时,它们的宽卷积具有交换性:
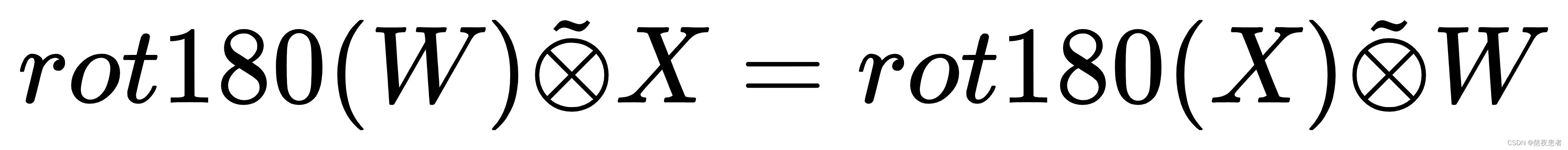
交换性证明:


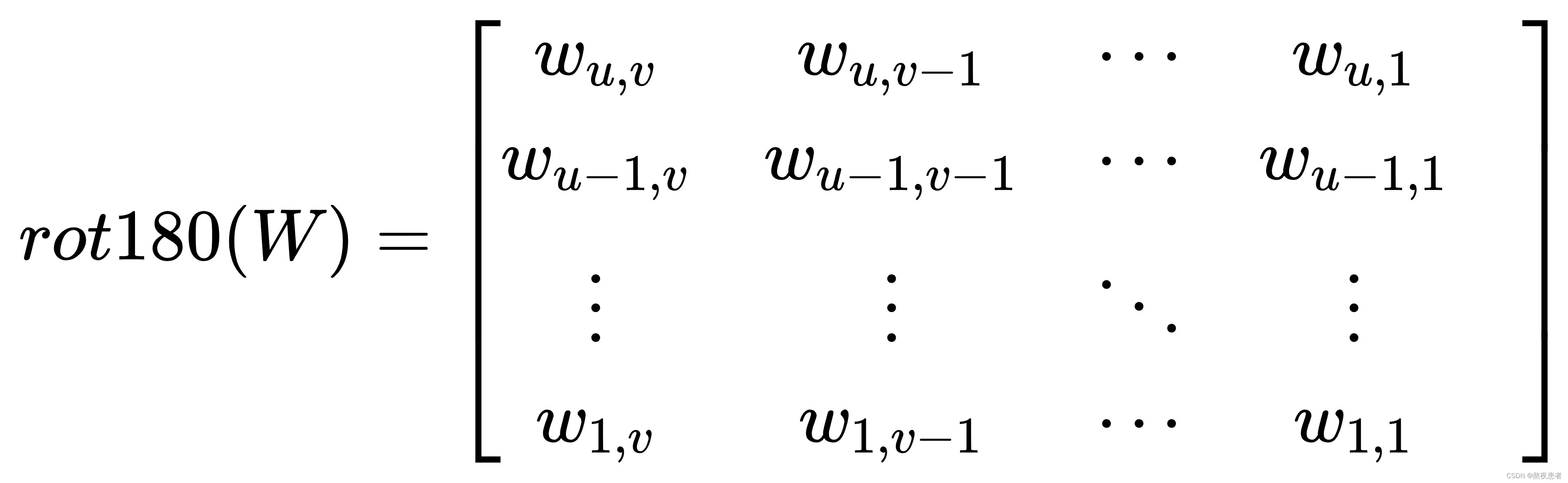
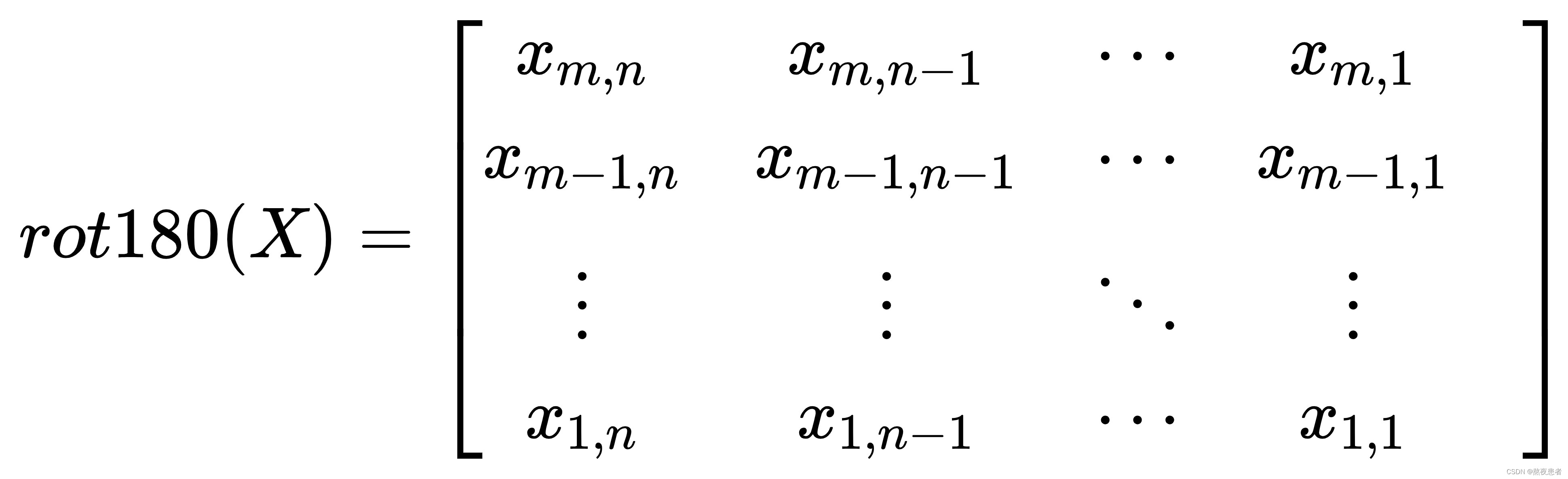
同时推导一下,我们发现:
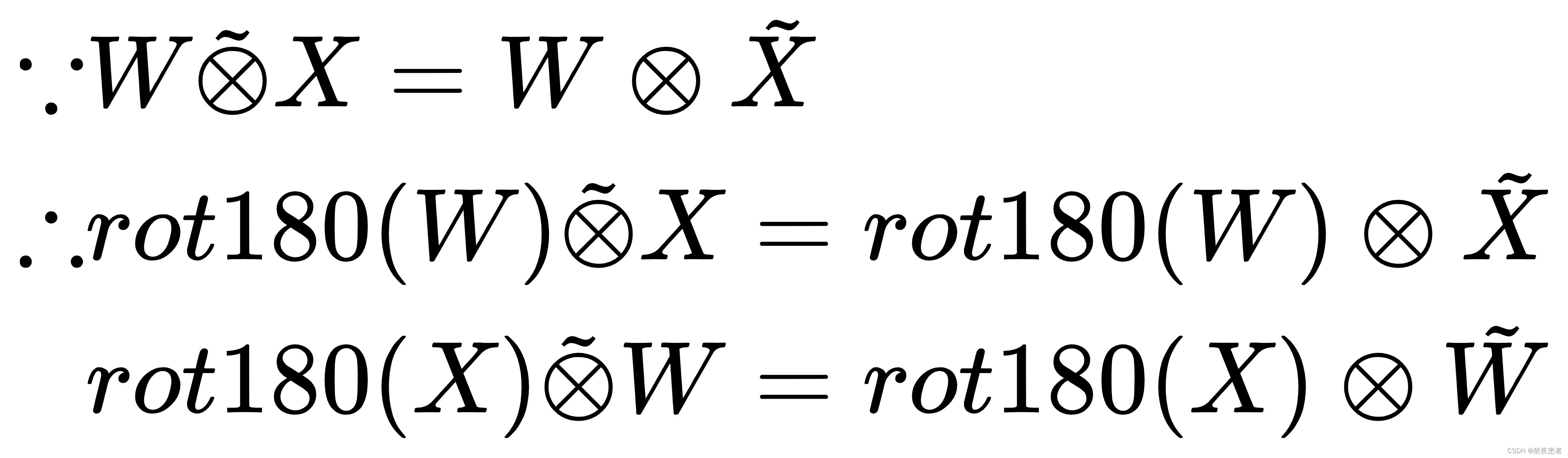
所以我们从证明![]() 变成证明
变成证明![]() 即可
即可




由此可见,交换性成立!照片感觉在这里展示不太好看,但是毕竟弄了大半天的东西。把照片源文件放进来可以自行下载观看
习题5-4 对于一个输入为100 × 100 × 256的特征映射组, 使用3 × 3的卷积核, 输出为100 × 100 × 256的特征映射组的卷积层, 求其时间和空间复杂度. 如果引入一个1 × 1卷积核, 先得到100 × 100 × 64的特征映射, 再进行3 × 3的卷积, 得到100 × 100 × 256的特征映射组, 求其时间和空间复杂度.
时间复杂度:因为映射后的图像的每一个像素都是经过卷积计算而来的,由这个想法开始,我们首先计算最后输出的图像像素点个数为个,并且卷积核大小为
,卷积核组是由256个卷积核构成的,所以每个像素点需要经过
次乘法运算(这里时间复杂度同代码,所以不考虑加法的效率)所以最好一共需要的时间效率为
空间复杂度为,因为这里考虑的都为代码过程的时间空间复杂度.
同理可以很容易求得另一组的答案如下:
时间复杂度:
空间复杂度:
习题5-5 对于一个二维卷积, 输入为3 × 3, 卷积核大小为2 × 2, 试将卷积操作重写为仿射变换的形式. 参见公式(5.45) .
关于这个问题之前的博客就提到过一些,但哪个时候就比较随性(不是好的习惯)了解的还不够透彻,经过老师上课的讲解对展开放射变化了解更为深刻了,首先引用鱼书中这一部分的讲解

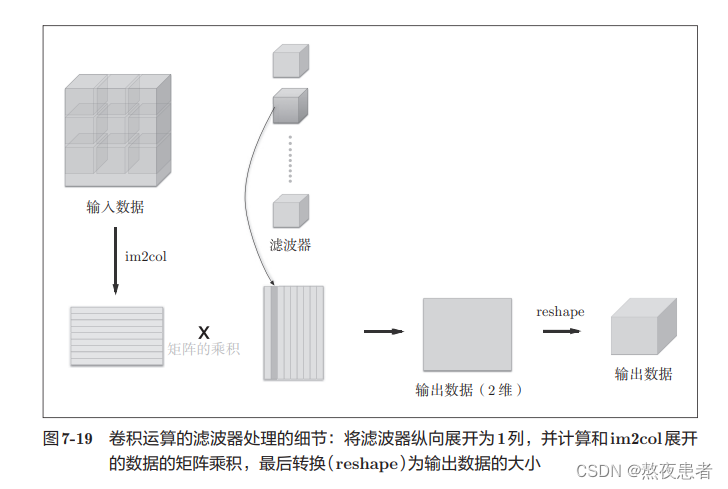
鱼书很明确的指出了,将滤波器展开为1列,那矩阵到底怎么展开呢,通过题目就可以很容易的明确了。

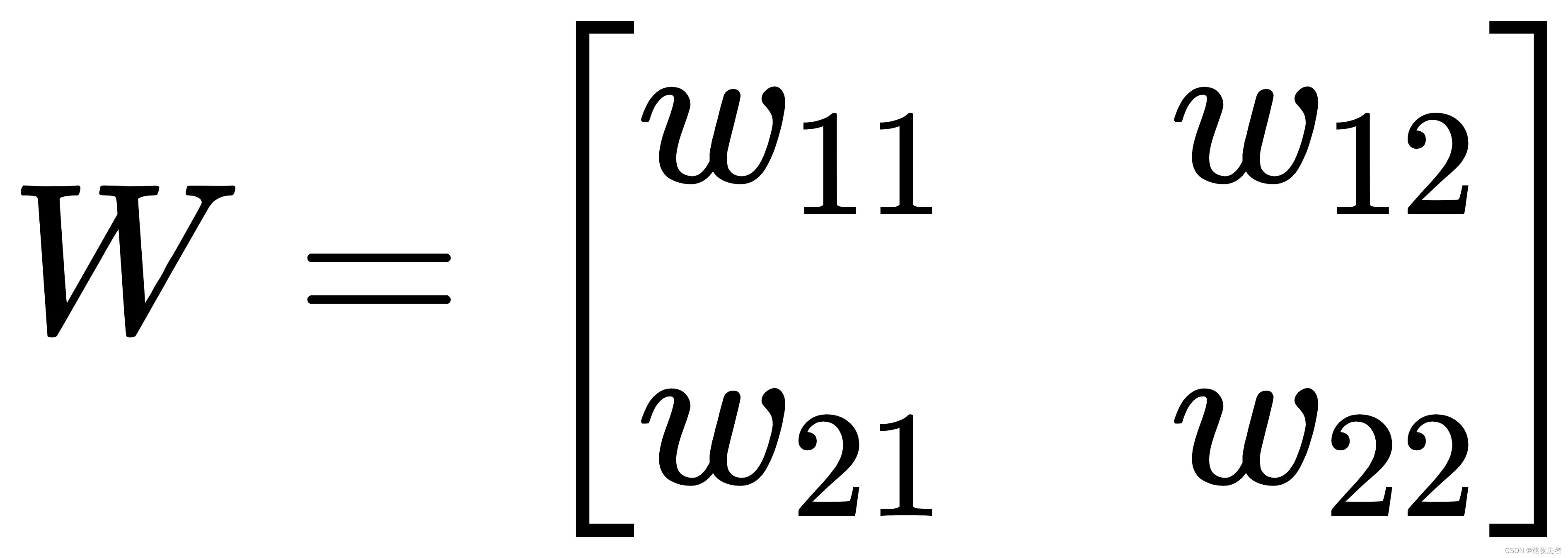
经过卷积操作仿射变化后,X,W变为如下:

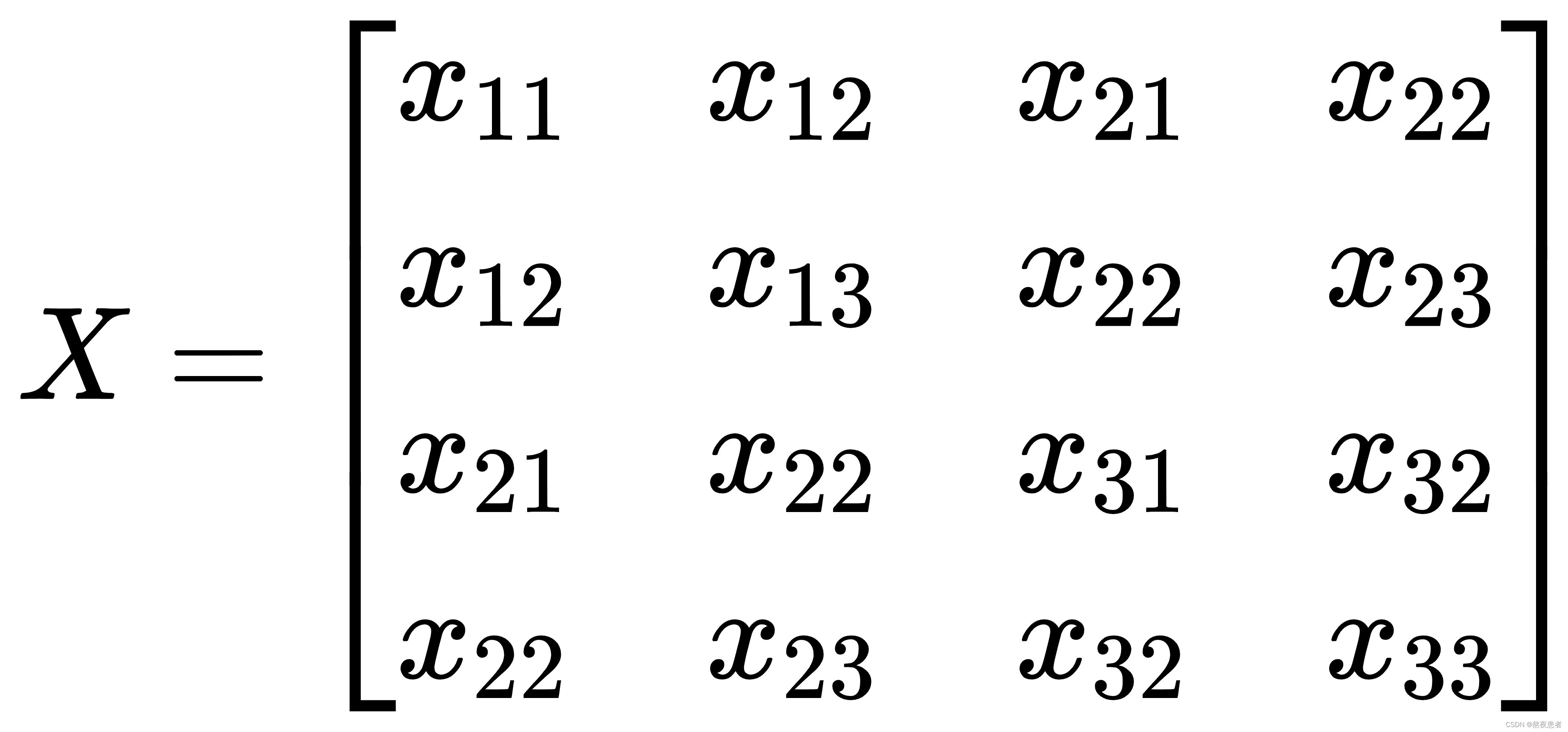
Y = X * W
这是鱼书中的例子,但是事实上还存在另一种放射变化,老师讲的不同于鱼书,将X拉成一列如下:
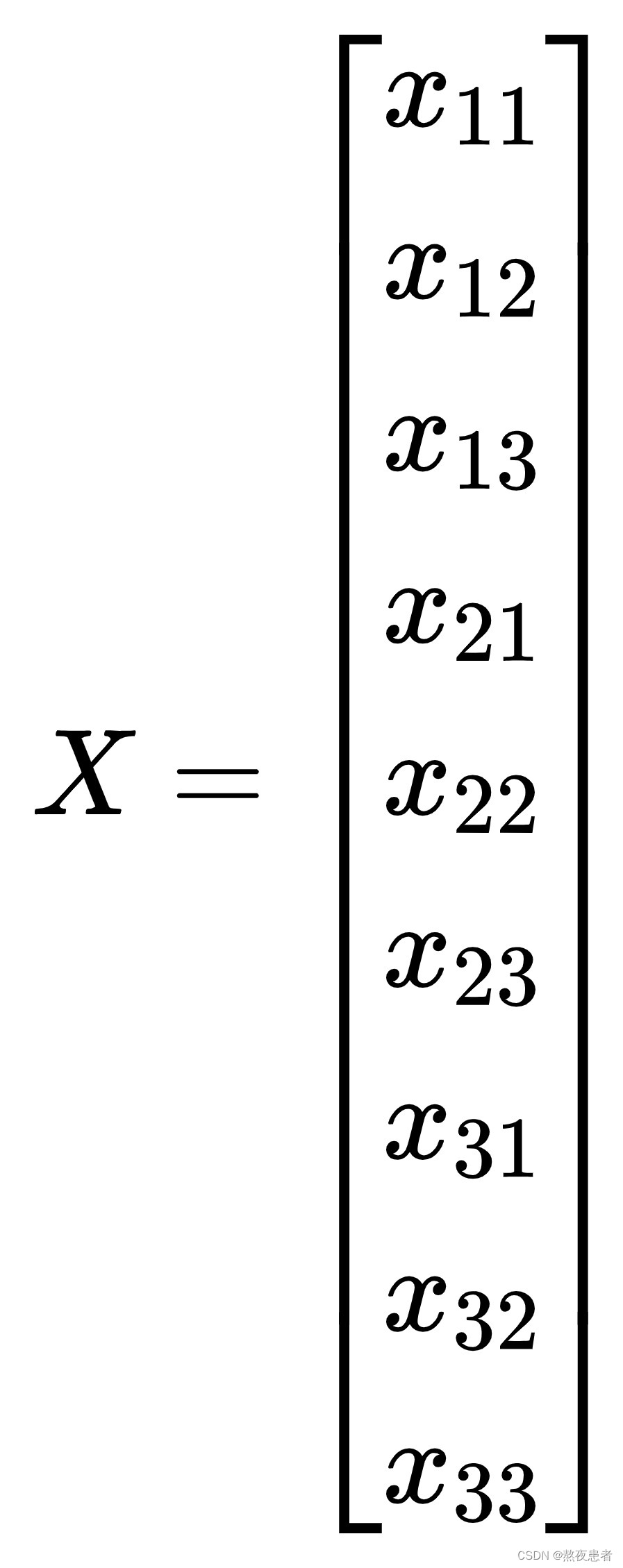

Y = W * X
两种仿射变化都是对的只是变现的形式不同罢了~
习题5-7 忽略激活函数,分析卷积网络中卷积层的前向计算和反向传播是一种转置关系
以一个3×3的卷积核为例,输入为X输出为Y
将4×4的输入特征展开为16×1的矩阵,y展开为4×1的矩阵,将卷积计算转化为矩阵相乘
因为:;并且
即
所以:
对比正向: ,所以两者是一种转置关系。
习题5-8 在空洞卷积中, 当卷积核大小为𝐾, 膨胀率为𝐷时, 如何设置零填充𝑃的值以使得卷积为等宽卷积 .
首先对于普通的卷积操作,输出特征图的大小由以下公式给出:

而在空洞卷积中,由于引入了膨胀率,上述公式需要做相应调整。空洞卷积的输出特征图大小的计算公式如下:
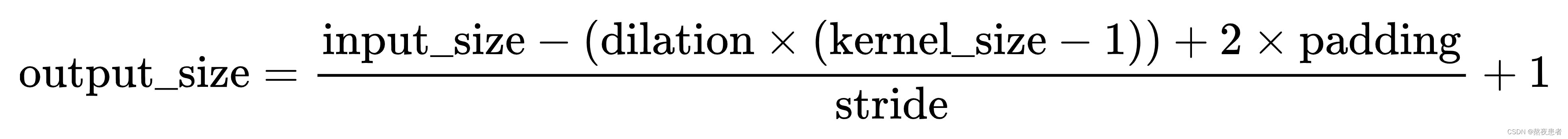
现在我们来解决问题,假设我们希望进行等宽卷积,即输入特征图的大小与输出特征图的大小相同。因此,我们可以令输出特征图的大小等于输入特征图的大小:
![]()
将这个等式代入空洞卷积的输出特征图大小计算公式中,可以得到:

接下来,我们可以解出零填充P的值:

PS:这两周大作业有点多,选修课还都结课,反向传播算法的手推,不太想随便糊弄一个,抄一抄没啥效果,所以手推的过程放在下周赶时间做一个,单独会再发个博客~