最长公共前缀

问题描述

编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀，返回空字符串 “”。详见leetcode14

问题分析

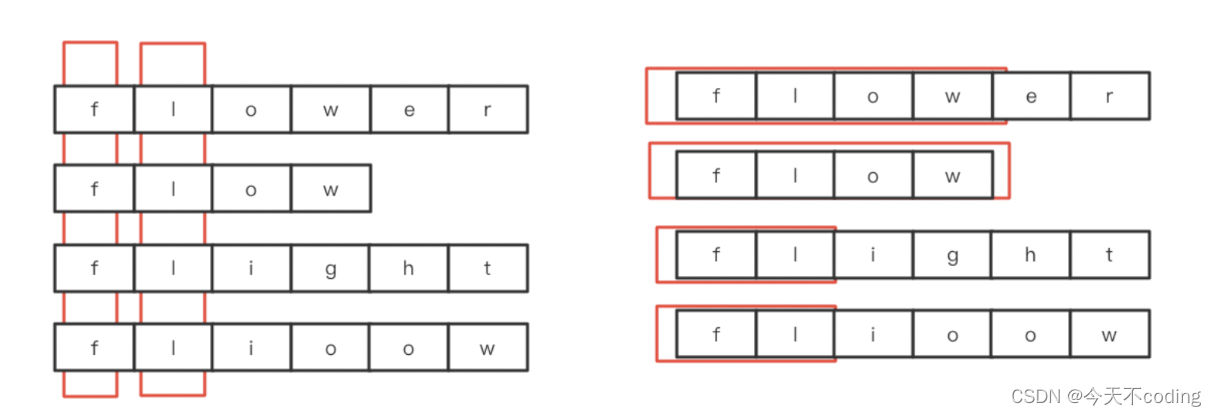
直观上来看，有竖直和水平两种方式，竖直方式是指我们依次比较所有字符串的第一个字符，如果相同，继续比较所有字符串的下一个字符，直至不相同或者有一个字符串遍历结束。水平方式是指可以先比较前两个字符的最长公共前缀，然后在比较前两个字符的最长公共前缀，与第三个字符的公共前缀，以此类推。同时，采用水平方式时，我们可以使用归并的方式，两两一组找最长公共前缀，然后再进行归并。

代码实现

竖直方式

public String longestCommonPrefix(String[] strs) {
    StringBuilder sb = new StringBuilder();
    int len = strs.length;
    int n = strs[0].length();
    for (int i = 0; i < n; i++) {
        char c = strs[0].charAt(i);
        for (int j = 1; j < len; j++) {
            if (i >= strs[j].length() || strs[j].charAt(i) != c){
                return sb.toString();
            }
        }
        sb.append(c);
    }
    return sb.toString();
}

水平方式

public String longestCommonPrefix(String[] strs) {
     int len = strs.length;
     if (len == 1) {
         return strs[0];
     }
     String prefix = longestCommonPrefix(strs[0], strs[1]);
     for (int i = 2; i < len; i++) {
         prefix = longestCommonPrefix(prefix, strs[i]);
     }
     return prefix;
 }

 public String longestCommonPrefix(String str1, String str2) {
     StringBuilder sb = new StringBuilder();
     int i = 0;
     int j = 0;
     while (i < str1.length() && j < str2.length()) {
         if(str1.charAt(i) == str2.charAt(j)){
             sb.append(str1.charAt(i));
             i++;
             j++;
         }else {
             return sb.toString();
         }
     }
     return sb.toString();
 }

压缩字符串

问题描述

给你一个字符数组 chars ，请使用下述算法压缩：
从一个空字符串 s 开始。对于 chars 中的每组 连续重复字符 ：
如果这一组长度为 1 ，则将字符追加到 s 中。
否则，需要向 s 追加字符，后跟这一组的长度。
压缩后得到的字符串 s 不应该直接返回 ，需要转储到字符数组 chars 中。需要注意的是，如果组长度为 10 或 10 以上，则在 chars 数组中会被拆分为多个字符。
请在 修改完输入数组后 ，返回该数组的新长度。
你必须设计并实现一个只使用常量额外空间的算法来解决此问题。
详见leetcode443

问题分析

可以设置两个指针，用于寻找重复字符的起始和结束位置，同时在设置一个指针，用于设置写入位置，遍历字符数组，但个字符直接追加，重复字符，写入当前字符和出现次数，对于两位以上的出现次数，可以先逆序写入，然后再反转

public int compress(char[] chars) {
    int left = 0;
    int right = 0;
    int write = 0;
    while (right < chars.length) {
        while (right < chars.length && chars[right] == chars[left]) {
            right++;
        }
        if (right - left == 1) {
            chars[write++] = chars[left];
            left = right;
        } else {
            int count = right - left;
            chars[write++] = chars[left];
            int start = write;
            while (count != 0) {
                int num = count % 10;
                chars[write++] = (char) ('0' + num);
                count/=10;
            }
            reverse(chars, start, write - 1);
            left = right;
        }
    }
    return write;
}
public void reverse(char[] chars, int left, int right) {
    while (left < right) {
        char temp = chars[left];
        chars[left] = chars[right];
        chars[right] = temp;
        left++;
        right--;
    }
}