1、复平面,复数的其它表示法
(1)几何表示法
直角平面坐标:
复平面
实轴,
虚轴

(2)向量表示法
向量
模:
复数加减法可用向量的三角形法则或者平行四边形法则
(3)结论
(两边之和大于第三边)
((两边之差大于第三边))
*辐角:向量和实轴正向的夹角称为
的辐角,记作
(有无穷多个,相差
)
*
*辐角主值:(
)
*当时,
,辅角不确定
| 1 | 实轴正向 | |||
| 2 | 第一象限 | |||
| 3 | 虚轴正向 | |||
| 4 | 第二象限 | |||
| 5 | 实轴负向 | |||
| 6 | 第三象限 | |||
| 7 | 虚轴负向 | |||
| 8 | 第四象限 |
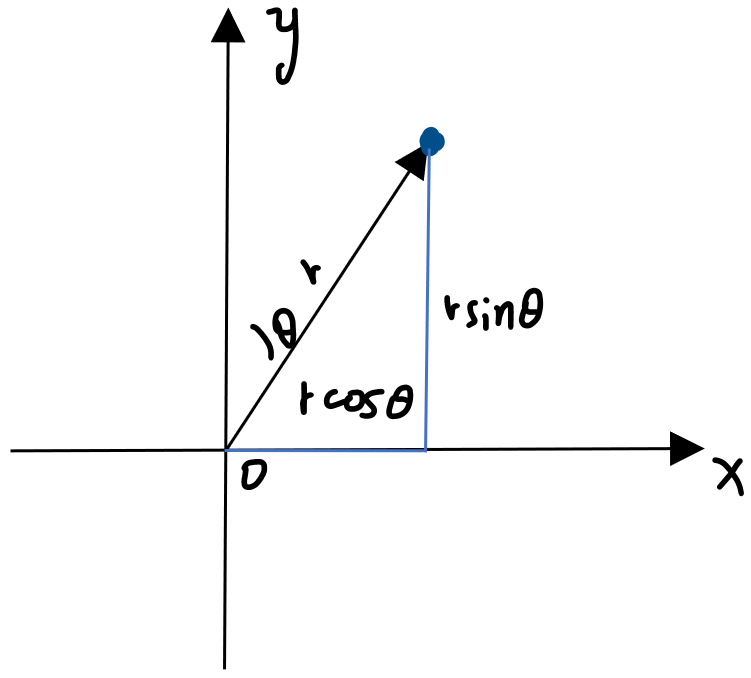
(4)三角表示法
*
*欧拉公式
*指数表示法
例题









![Educational Codeforces Round 158 [Rated for Div. 2]](https://img-blog.csdnimg.cn/353b8ec9f5e74f9faa7c7b8532a56c99.png)