Problem - D - Codeforces

翻译：

Monocarp有一棵树，它由𝑛个顶点组成，并以顶点1为根。他决定研究BFS(宽度优先搜索)，所以他在他的树上运行BFS，从根开始。BFS可以用下面的伪代码描述:

A =[] #处理顶点的顺序
q = Queue()
Q.put(1) #将根放在队列的末尾
而不是q.empty():
K = q.pop() #从队列中检索第一个顶点
A.append (k) #将k追加到访问顶点序列的末尾
对于y ing [k]: # g[k]是顶点k的所有子节点的列表，按升序排序
q.put (y)
Monocarp对BFS非常着迷，以至于最后失去了他的树。幸运的是，他仍然有一个顶点序列，其中BFS算法访问了顺序顶点(伪代码中的数组a)。Monocarp知道每个顶点只被访问过一次(因为它们只被从队列中取出一次)。此外，他知道每个顶点的所有子结点都是按升序查看的。

Monocarp知道有很多树(在一般情况下)具有相同的访问顺序𝑎，所以他不希望恢复他的树。单果树适用于任何高度最小的树。

树的高度是树顶点的最大深度，顶点的深度是从根结点到顶点的路径中的边数。例如，顶点1的深度是0，因为它是根结点，所有根结点的子结点的深度都是1。

帮助Monocarp找到任何给定访问顺序𝑎和最小高度的树。

输入
第一行包含一个整数𝑡(1≤𝑡≤1000)——测试用例的数量。

每个测试用例的第一行包含一个整数𝑛(2≤𝑛≤2⋅105)——树中的顶点数。

每个测试用例的第二行包含𝑛整数𝑎1𝑎2,…,𝑎𝑛(1≤𝑎𝑖≤𝑛;𝑎𝑖≠𝑎𝑗;𝑎1=1)- BFS算法访问顶点的顺序。

可以保证𝑛除以测试用例的总和不超过2⋅105。

输出
对于每个测试用例，以给定的访问顺序𝑎打印树的最小可能高度。

例子
inputCopy
3.
4
1 4 3 2
2
1 2
3.
1 2 3
outputCopy
3.
1
1
请注意
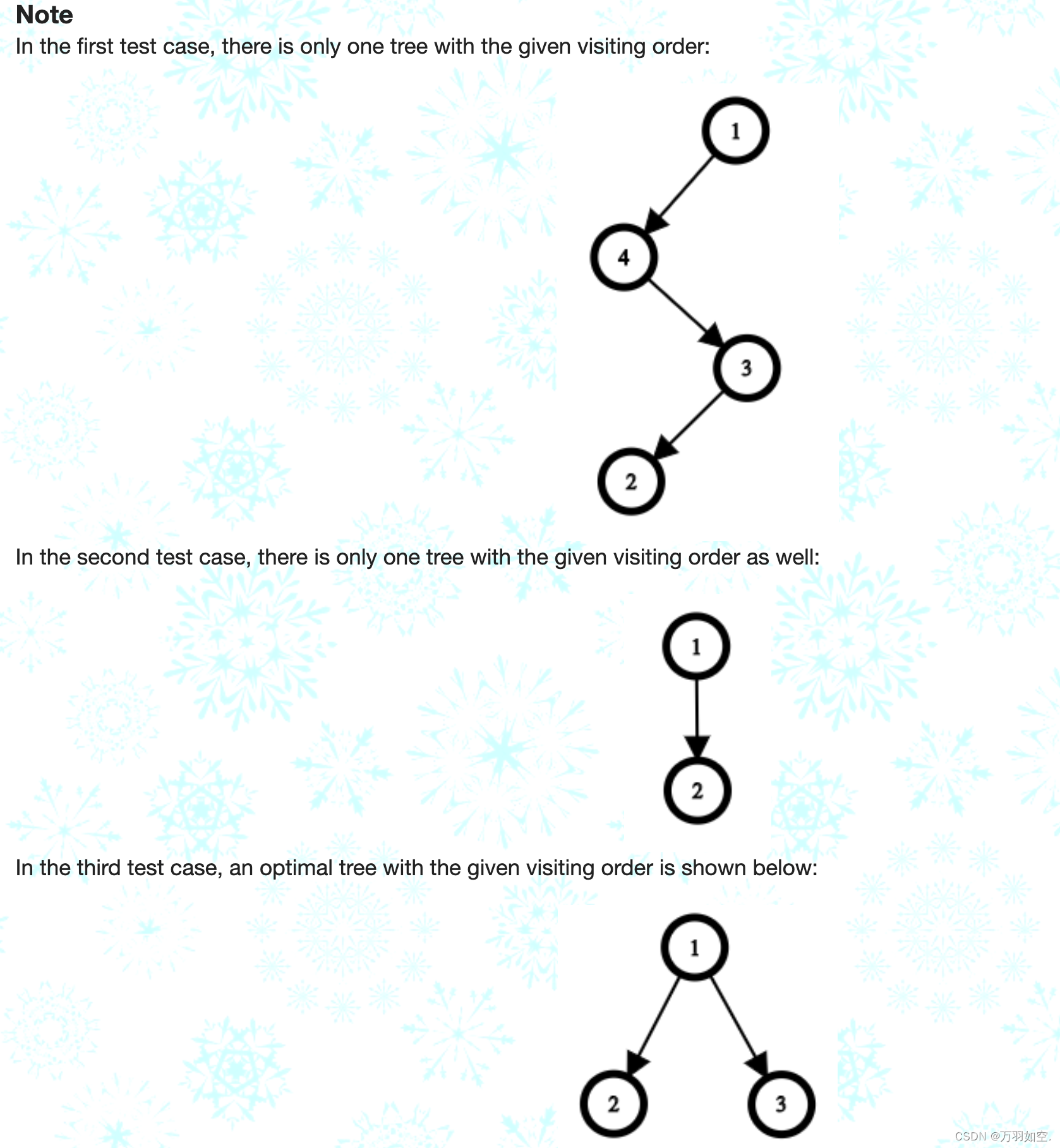
在第一个测试用例中，只有一棵树具有给定的访问顺序:

在第二个测试用例中，给定的访问顺序也只有一棵树:

在第三个测试用例中，给定访问顺序的最优树如下所示:

思路：求树的最小高度，按给定访问顺序。如果是按着递增来，我们就可以给它分叉，如果逆序就不得不再开一层。可以手动画图模拟一下，就会很清晰。我们来模拟这个过程，等到每个分叉都开展完，再进行下一层。看代码可能清晰一些。

代码：

/*Looking! The blitz loop this planet to search way
 
 Only my RAILGUN can shoot it 今すぐ
 
 身体中を  光の速さで
 
 駆け巡った確かな予感
 
 掴め！ 望むものなら残さず
 
 輝ける自分らしさで
 
 信じてるよ  あの日の誓いを
 
 この瞳に光る涙それさえも  強さになるから
 
 */
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long  ll;
int n,t;
inline __int128 read(){
    __int128 x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
inline void print(__int128 x){
    if(x < 0){
        putchar('-');
        x = -x;
    }
    if(x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}

int ap[200005];
int lllld=1;
void wanyurukong(){
    cin>>n;
    for (int i=1 ; i<=n; i++) {
        cin>>ap[i];
    }
    int ans=1;
    int ff=0;
    int fc=0;
    int las=1;
    for (int i =2; i<=n; i++) {
        if (ap[i]>ap[i-1]) {
            fc++;
        }
        else{
            ff++;
            if (ff==las) {
                las=fc;
                ans++;
                ff=0;
            }
//            printf("%d  %d %d\n",i,ans,las);
        }
    }
//    printf(" %d  %d\n",lllld,ans);
    printf("%d\n",ans);
  
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(); cout.tie();
    cin>>t;
    while (t--) {
        wanyurukong();
    }
    //wanyurukong
    return 0;
}