哈夫曼树是不定长编码方式,由于是将权值大的元素放在离根结点近的地方 ,权值小的放在离根远的地方,哈夫曼树效率很高,并且一个编码不会以另一个编码作为前缀,避免了编码的歧义性,本文将带大家探索如何创建和使用哈夫曼树。

构造哈夫曼树
n个元素构造哈夫曼树需要2n-1个结点,为什么是这个结果呢?接下来我们看一下哈夫曼树的构造原理
- 从所有(未确定双亲结点)元素中选出两个权值最小的元素
- 选出来的元素的权值的和为新的元素的权值(新的元素将是这两个元素的双亲结点),再将新的元素放入原来的元素集合中(已经确定双亲结点则不用放回集合中),现在集合中元素数量-1,但总元素个数+1,因为新生成了一个元素。
- 重复 1,2过程,直到元素集合中只有1个元素。
很容易看出总共要重复n-1次1,2操作(因为每次操作后集合元素数量要-1,当集合元素的数量为2时就是最后一次操作,此时总共进行了n-1次操作)每进行一次操作都会生成一个新元素,所以总共生成了n-1个新元素,再加上原来的元素,总共2*n-1个。
这里我们用结构体数组维护哈夫曼树,清楚原理后我们来看下具体代码:

#include <iostream>
using namespace std;
//最大元素个数
const int N=1e5;
typedef struct{
int parent;
int lchild,rchild;
int weight;
}HuffNode,*HUffTree;
//第0个位置不使用,下标从1开始
HuffNode tree[N*2];
void HuffMan(HuffNode tree[],int w[],int n){
//p1最小的权值的结点索引,p2第二小的结点的索引
int i,j,p1,p2;
int small1,small2;
//要求最小值,所以初始化要赋很大的值
small1=small2=0x3fff;
//初始化每个结点
for(i=1;i<=n;i++){
tree[i].weight=w[i];
tree[i].parent=0;
tree[i].lchild=0;
tree[i].rchild=0;
}
//初始化其他结点
for(;i<2*n;i++){
tree[i].parent=0;
tree[i].lchild=0;
tree[i].rchild=0;
}
for(i=n+1;i<2*n;i++){
for(j=1;j<i;j++){
//如果结点的双亲结点为0,说明改结点还在元素集合中
if(tree[i].parent==0){
if(tree[i].weight<small1){
//已经找到一个比原来最小的元素还小的元素,那原来最小的现在成了第二小
small2=small1;
p2=p1;
//更新最小元素
small1=tree[i].weight;
p1=j;
}
else if(tree[i].weight<small2){
small2=tree[i].weight;
p2=j;
}
}
}
//找到权值最小的两个结点后,要生成新的结点
tree[i].weight=small1+small2;
tree[i].lchild=p1;
tree[i].rchild=p2;
//更新最小的两个结点的双亲为新结点
tree[p1].parent=tree[p2].parent=i;
}
}
哈夫曼树编码
在已经建好的哈夫曼树上,从叶子结点开始沿着双亲结点找根,每退回一步就到了一个分支,从而得到一位哈夫曼编码的值。因为每一个字符的哈夫曼编码都是根结点到叶子结点的路径分支上的0、1序列,所以先得到的编码是低位码,后得到的是高位码,可以设置二维字符数组来保存每个哈夫曼编码。
char HuffManCode[N][N];
void huffmancodding(HuffNode tree[],int n){
//存储每次循环后字符的哈夫曼编码
char * tem = (char*)malloc(n*(sizeof(char)));
int parent;
//结束标志
tem[n-1] = '\0';
//叶子结点是前n个结点
for(int i =1;i<=n;i++){
int idx=n-1;
for(int j =i;tree[j].parent!=0;j=tree[j].parent){
//得到双亲结点
parent = tree[j].parent;
//左分支为 0,右分支为 1
if(tree[parent].lchild==j){
tem[--idx]='0';
}
else{
tem[--idx]='1';
}
}
//在C语言中,数组是一个连续存储的数据结构,其中每个元素都有一个固定的地址。数组名实际上是指向数组第一个元素的指针。
//对于二维数组b[n][m],它实际上是按行优先或列优先的方式在内存中进行存储的一维数组。
// 因此,b[i]实际上是代表了第i+1行(如果从0开始计数)的首地址,也就是指向这一行第一个元素的指针。
strcpy(HuffManCode[i],&tem[idx]);
}
free(tem);
for(int i =1;i<=n;i++)
printf("%d: %s\n",i,HuffManCode[i]);
}
测试
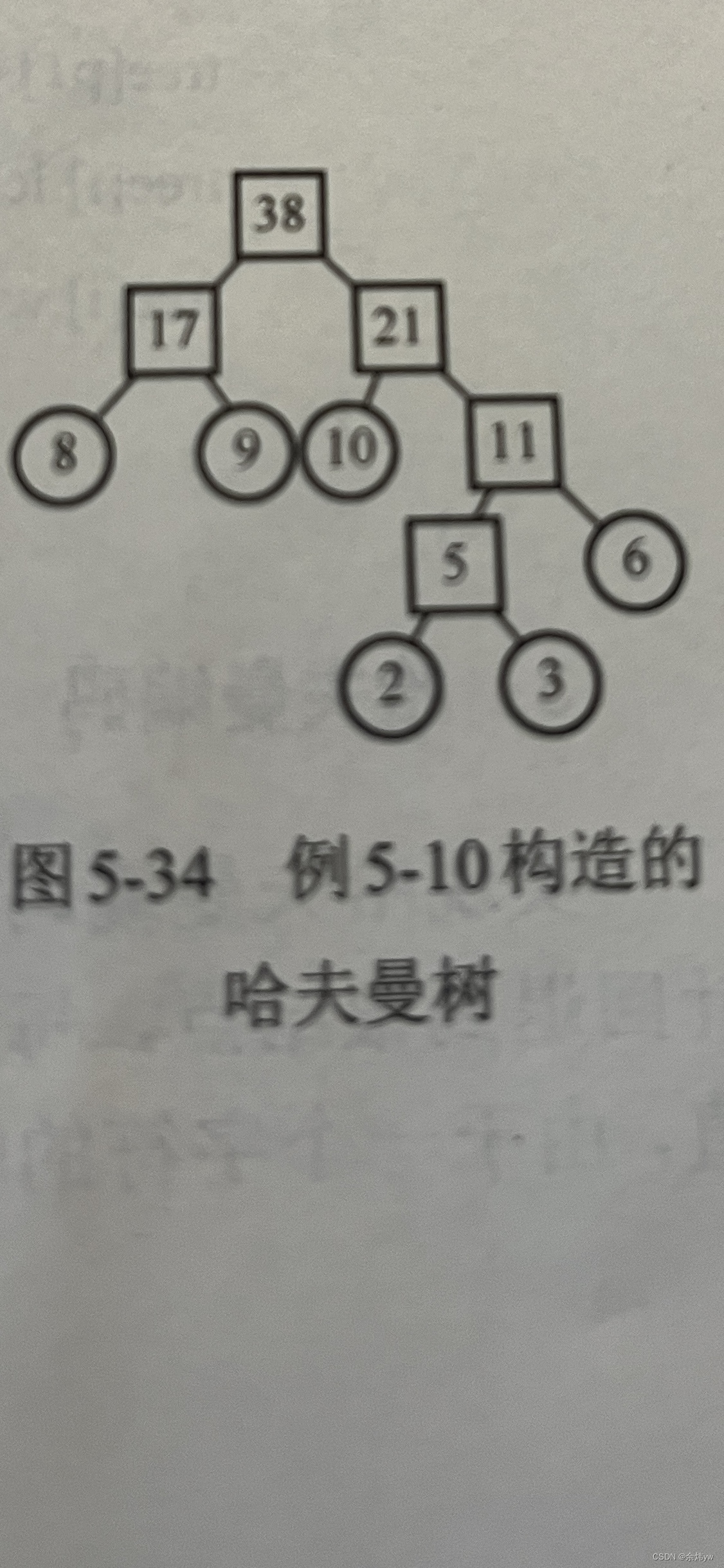
按照这个图来检验一下我们的代码

#include <iostream>
#include <cstring>
using namespace std;
//最大元素个数
const int N=100;
typedef struct{
int parent;
int lchild,rchild;
int weight;
}HuffNode;
//第0个位置不使用,下标从1开始
HuffNode tree[N*2];
void HuffMan(HuffNode tree[],int w[],int n){
//p1最小的权值的结点索引,p2第二小的结点的索引
int i,j,p1,p2;
int small1,small2;
//要求最小值,所以初始化要赋很大的值
small1=small2=0x3fff;
//初始化每个结点
for(i=1;i<=n;i++){
tree[i].weight=w[i];
tree[i].parent=0;
tree[i].lchild=0;
tree[i].rchild=0;
}
//初始化其他结点
for(;i<2*n;i++){
tree[i].parent=0;
tree[i].lchild=0;
tree[i].rchild=0;
}
for(i=n+1;i<2*n;i++){
small1=small2=0x3fff;
for(j=1;j<i;j++){
//如果结点的双亲结点为0,说明改结点还在元素集合中
if(tree[j].parent==0){
if(tree[j].weight<small1){
//已经找到一个比原来最小的元素还小的元素,那原来最小的现在成了第二小
small2=small1;
p2=p1;
//更新最小元素
small1=tree[j].weight;
p1=j;
}
else if(tree[j].weight<small2){
small2=tree[j].weight;
p2=j;
}
}
}
//找到权值最小的两个结点后,要生成新的结点
tree[i].weight=small1+small2;
tree[i].lchild=p1;
tree[i].rchild=p2;
//更新最小的两个结点的双亲为新结点
tree[p1].parent=tree[p2].parent=i;
}
}
char HuffManCode[N][N];
void huffmancodding(HuffNode tree[],int n){
//存储每次循环后字符的哈夫曼编码
char * tem = (char*)malloc(n*(sizeof(char)));
int parent;
//结束标志
tem[n-1] = '\0';
//叶子结点是前n个结点
for(int i =1;i<=n;i++){
int idx=n-1;
for(int j =i;tree[j].parent!=0;j=tree[j].parent){
//得到双亲结点
parent = tree[j].parent;
//左分支为 0,右分支为 1
if(tree[parent].lchild==j){
tem[--idx]='0';
}
else{
tem[--idx]='1';
}
}
//在C语言中,数组是一个连续存储的数据结构,其中每个元素都有一个固定的地址。数组名实际上是指向数组第一个元素的指针。
//对于二维数组b[n][m],它实际上是按行优先或列优先的方式在内存中进行存储的一维数组。
// 因此,b[i]实际上是代表了第i+1行(如果从0开始计数)的首地址,也就是指向这一行第一个元素的指针。
strcpy(HuffManCode[i],&tem[idx]);
}
free(tem);
for(int i =1;i<=n;i++)
printf("%d: %s\n",i,HuffManCode[i]);
}
int main(){
int w[7]={0,6,2,3,9,10,8};
HuffMan(tree,w,6);
huffmancodding(tree,6);
}

总结
本文介绍了哈夫曼树的创建和如何编码,希望本文能帮助到正在学习哈夫曼树的读者。