这里写目录标题
- TD跟踪微分器
- ESO
- NLSEF
- 后续把公式的核心原理分析一下
参考链接:ADRC自抗扰控制,有手就行
ADRC是升级版的PID,由TD(跟踪微分器),ESO(扩张状态观测器),NLSEF(非线性控制律)。
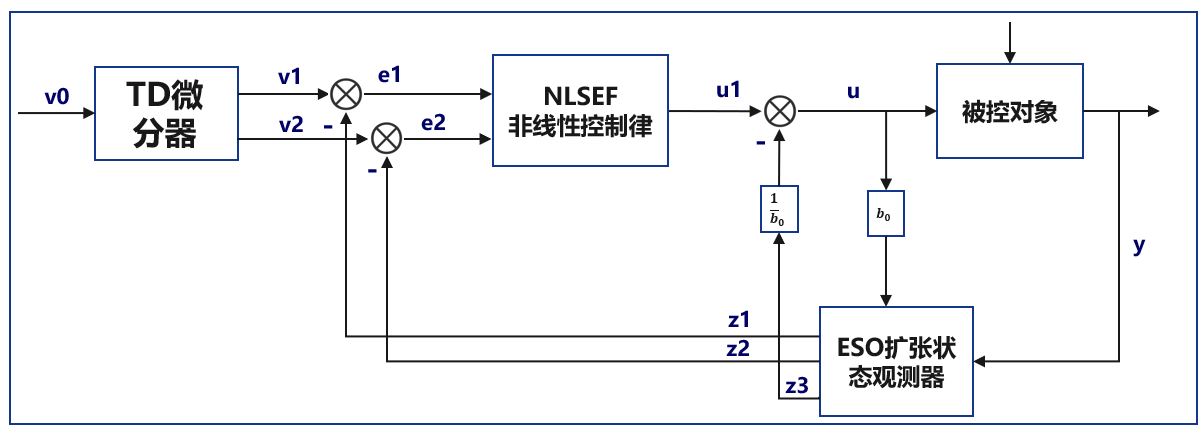
其中TD主要是为了防止目标值突变而安排的过渡过程,ADRC的灵魂在于ESO,NLSEF则是改良PID直接线性加权(输出=比例+积分+微分)而引进的非线性控制律,使其更符合非线性系统。
TD跟踪微分器

在c++中的实现为:
fhan函数
#include <iostream>
#include <cmath>
float sign(float x)
{
if(x>0)
return 1;
else if(x<0)
return -1;
else
return 0;
}
float fhan(float x1,float x2,float r,float h)
float deltaa =0,
deltaa0 =0,
y =0,
a0 =0,
a =0,
fhan =0;
deltaa = r*h;
deltaa0 = deltaa*h;
y=x1+x2*h;
a0 = sqrtf(deltaa*deltaa+8*r*fabsf(y));
if(fabsf(y)<=deltaa0)
a=x2+y/h;
else
a=x2+0.5*(a0-deltaa)*sign(y);
if(fabsf(a)<=deltaa)
fhan = -r*a/deltaa;
else
fhan = -r*sign(a);
return fhan;
}
ESO

c++代码为:
/*******************************fal函数**********************************/
float fal(float e,float alpha,float delta)
{
float result = 0,fabsf_e = 0;
fabsf_e = fabsf(e);
if(delta>=fabsf_e)
result = e/powf(delta,1.0-alpha);
else //if(delta<fabsf_e)
result = powf(fabsf_e,alpha)*sign(e);
return result;
}
NLSEF

反应到程序上就是:
u0 = belta1*fal(e1,alpha1,delta) + belta2*fal(e2,alpha2,delta);//其中0<alpha1<1<alpha2
u = u0 - z3/b;
return u;
后续把公式的核心原理分析一下
然后就是参数整定的过程:
参数整定的规律是先将TD参数整定好,再整定ESO和NLSEF。
TD的参数整定是最简单的,观测v1的输出和输入v0的线性,其跟随的快慢并没有规定一定要多快多慢,取决于你想要的效果。TD参数只有两个:快速因子r 和滤波因子h 。其中,r 与跟踪速度呈正相关,然而,随之带来的是噪声放大的副作用;h与滤波效果呈正相关,但当h增大时,跟踪信号的相位损失也会随之增加。滤波因子经常取值为ADRC控制周期,比如1ms调用一次,h就是0.001,这也不是死定的,可以根据自己的效果做细微调整。
ESO共有b、delta、belta01、belta02、belta03共5个参数,其中delta取值范围在5h<=delta<=10h,h为ADRC控制周期。参数整定可以先将b定下来,比如取1或者2(最好还是能够知道你的二阶系统系数),然后先后调整belta01、belta02、belta03,观测z1能不能够很好的跟随反馈y,如果是,那么大概参数就调好了;如果不是,可以改动一下b,还是不行的话就得认认真真的检测一下反馈y是不是出了什么问题,比如变量数据类型转换有没有做好。如果懂得自己在输出中加入随机数(白噪声),注意幅值不能过大,观测一下z3是不是能够很好的观测到随机扰动。若以上两个条件都成立,那么ADRC就几乎被整定好了。
NLSEF参数有alpha1,alpha2,belta1,belta2四个,其中0<alpha1<1<alpha2。belta1和belta2则视效果而定,通常ESO和NLSEF一起调,在整定ESO参数时,可以先把delta1和delta2定为1,再调ESO,待ESO有一定效果后,反复调整ESO参数无果,可以加入NLSEF参数整定,取得更好的效果。