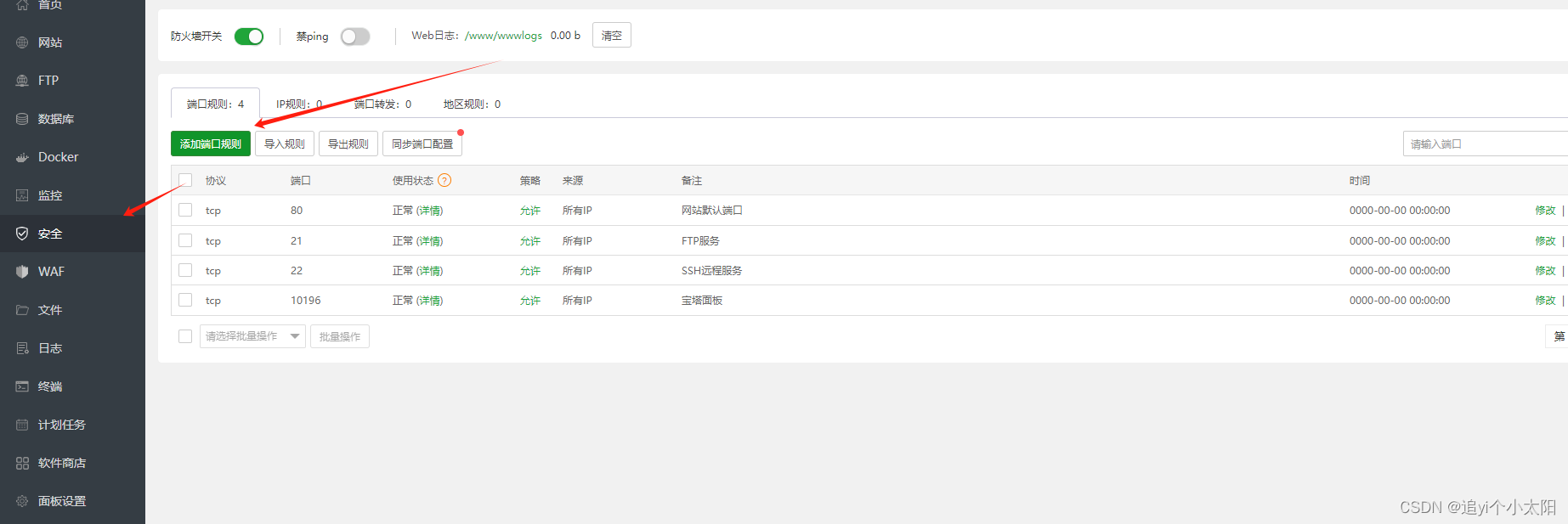
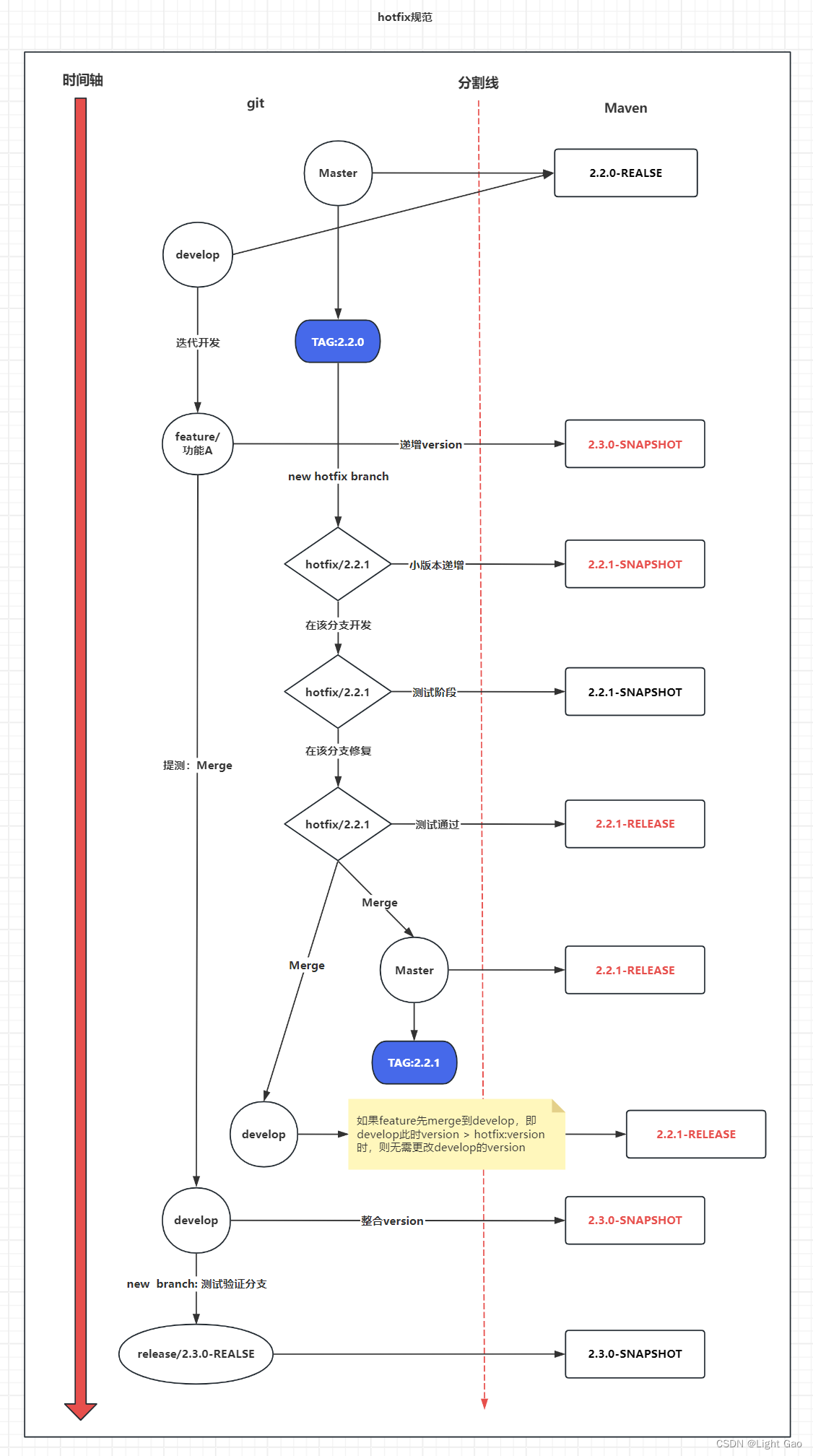
没没没没没没没错,这是一道简单的递归(其实是深搜加回溯)
我不管,我说是递归就是递归。
上题干:
题目描述
排列与组合是常用的数学方法,其中组合就是从 n 个元素中抽出 r个元素(不分顺序且 r≤n),我们可以简单地将 n 个元素理解为自然数 1,2,…,n,从中任取 r 个数。
现要求你输出所有组合。
例如 n=5,r=3,所有组合为:
123,124,125,134,135,145,234,235,245,345123,124,125,134,135,145,234,235,245,345。
输入格式
一行两个自然数n,r(1<n<21,0≤r≤n)。
输出格式
所有的组合,每一个组合占一行且其中的元素按由小到大的顺序排列,每个元素占三个字符的位置,所有的组合也按字典顺序。
注意哦!输出时,每个数字需要 3 个场宽。以 C++ 为例,你可以使用下列代码:
cout << setw(3) << x;输出占 3 个场宽的数 x。注意你需要头文件
iomanip。输入输出样例
输入 #1复制
5 3输出 #1复制
1 2 3 1 2 4 1 2 5 1 3 4 1 3 5 1 4 5 2 3 4 2 3 5 2 4 5 3 4 5
我现在再次重复一遍:写递归,请你放空你的脑袋,然后用样例,画出一个草图,然后用最简单的(最暴力的)思路去想。不要想太细,太复杂。等你把递归的框架搭建完了,再去思考边界。
认真看题目啊喂,由于题目要求,每一组数必须是从小到大的排列,所以当第二个数是5的时候,后面没有比5更大的,所以这种组合就不存在。
第一步,让我们轻轻画一个草图:
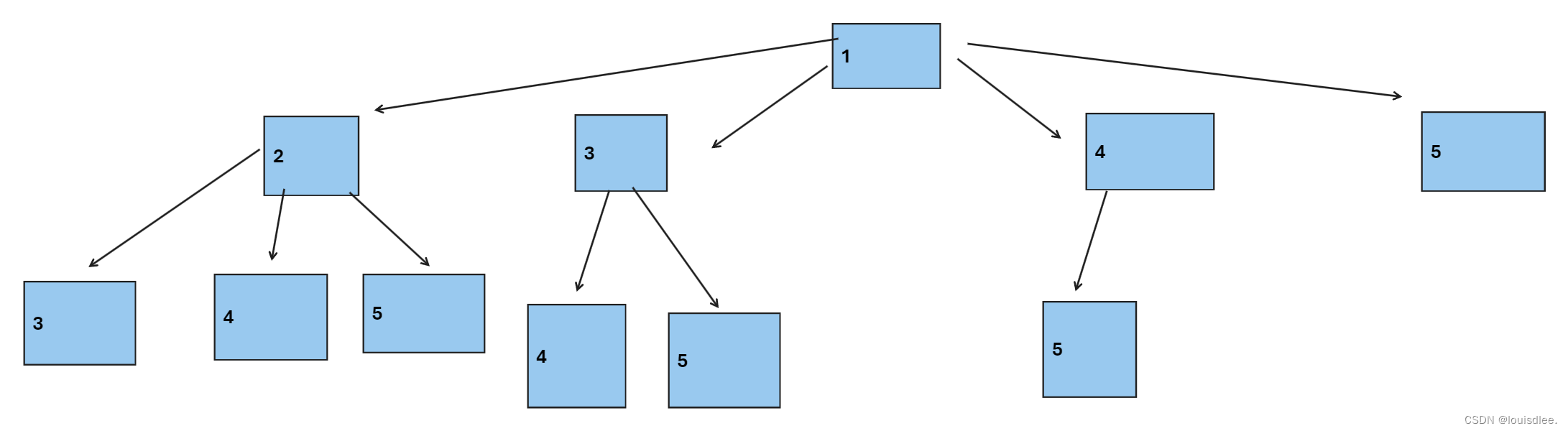
这个就是以1为开头的,所有排列组合
再说一遍:递归题,不要想太多,画出一个例子就可以了,想太多,越想越乱。
第二步,根据图像想一个巨巨巨巨巨朴素的思路(最暴力的)
我们从1开始往下找,一共要找3个数字.
先找下一层最左边的,是2,此时序列就是1,2。
由于我们要字典序(不知道字典序是什么的,看一下样例给的答案。)(也就是 1 2 3 必须要在 1 2 4 前面, 2 3 4 必须 要在 2 3 5前面,这样的排序,不过多解释)从小到大,
所以我们直接递归到下一层,从下一层的最左边开始(最左边最小),
此时的序列就是1,2,3。
打印序列,向逐渐增大移动,序列变为1,2,4 继续移动,序列变成1,2,5
当没有数了之后,回到上一层
当 2的下一层都找完了,,继续向2这一层数字增大的方向走,也就是1,2变成1,3。
重复此过程。
ok,思路非常简单,我想你们应该也能想到这样做,如果大体能看懂,那也很不错了,相信阅读完本栏目之后,你能不害怕递归。
直接上代码就完事了:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
#include<string>
#include<algorithm>
#include<vector>
#include<cctype>
#include<map>
#include<set>
#include<queue>
#include<numeric>
#include<iomanip>
using namespace std;
const int N = 30;
int t[N];
int flag[N];
int n, r;
void dfs(int x,int y) {
if (y > r ) { 当前序列里面的数字个数大于r的时候,就停止
for (int i = 1; i <= r; i++) { 打印答案
cout << setw(3) << t[i];
}
cout << endl;
return;
}
for (int i = x ; i <= n; i++) 从x开始,保证后面存进来的每一个数都大于x
if (flag[i] == 0 ) { 如果i被标记过了,那么我们就不管i,如果没有,就把i加入到序列里面
flag[i] = 1; 标记i
t[y] = i; 把i加入到序列里面
dfs(i + 1, y + 1); 递归下一个数
flag[i] = 0; 递归结束之后,恢复标记
}
}
int main() {
cin >> n>>r;
dfs(1, 1); //递归从1开始,第二个1代表序列里面只有1个数字
}多么简单的一道递归啊。