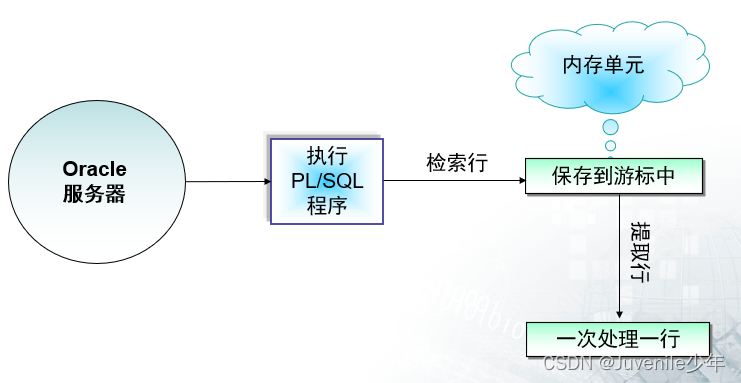
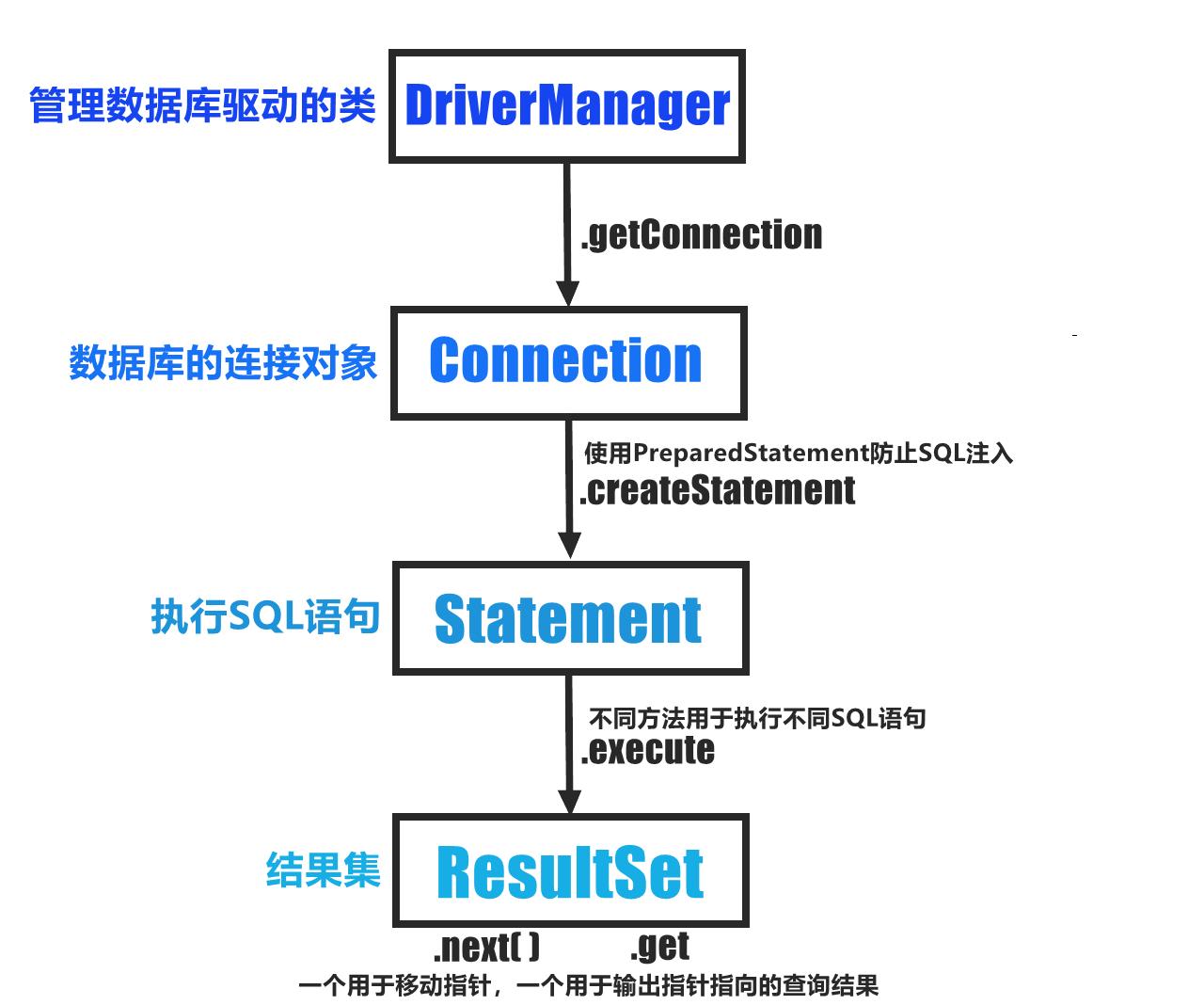
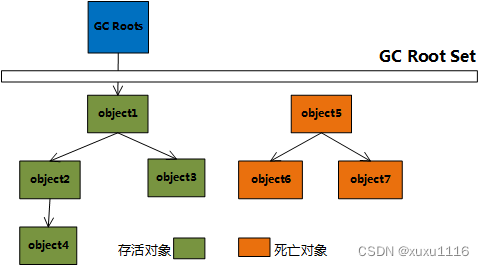
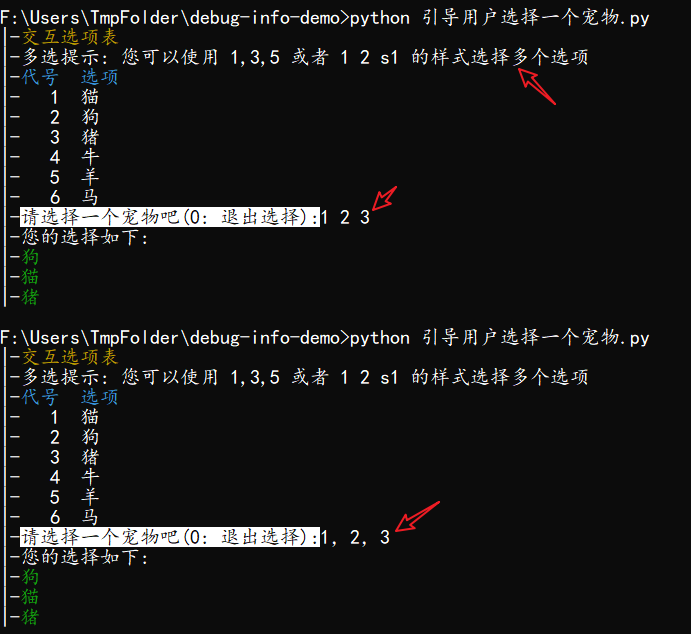
查询（自主提示）和键（非自主提示）之间的交互形成了注意力汇聚； 注意力汇聚有选择地聚合了值（感官输入）以生成最终的输出。 本节将介绍注意力汇聚的更多细节， 以便从宏观上了解注意力机制在实践中的运作方式。 具体来说，1964年提出的Nadaraya-Watson核回归模型 是一个简单但完整的例子，可以用于演示具有注意力机制的机器学习。

import torch
from torch import nn
from d2l import torch as d2l

生成数据集

在这里生成了50个训练样本和\(50\)个测试样本。 为了更好地可视化之后的注意力模式，需要将训练样本进行排序。

n_train = 50  # 训练样本数
x_train, _ = torch.sort(torch.rand(n_train) * 5)   # 排序后的训练样本

def f(x):
    return 2 * torch.sin(x) + x**0.8

y_train = f(x_train) + torch.normal(0.0, 0.5, (n_train,))  # 训练样本的输出
x_test = torch.arange(0, 5, 0.1)  # 测试样本
y_truth = f(x_test)  # 测试样本的真实输出
n_test = len(x_test)  # 测试样本数
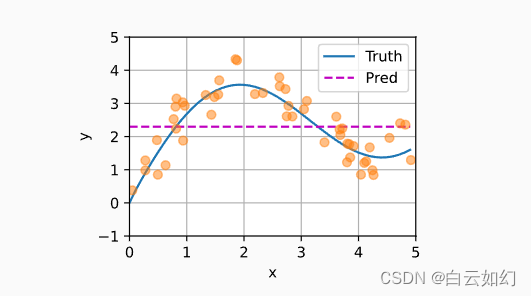
n_test

下面的函数将绘制所有的训练样本（样本由圆圈表示）， 不带噪声项的真实数据生成函数\(f\)（标记为“Truth”）， 以及学习得到的预测函数（标记为“Pred”）。

def plot_kernel_reg(y_hat):
    d2l.plot(x_test, [y_truth, y_hat], 'x', 'y', legend=['Truth', 'Pred'],
             xlim=[0, 5], ylim=[-1, 5])
    d2l.plt.plot(x_train, y_train, 'o', alpha=0.5);

平均汇聚

如下图所示，这个估计器确实不够聪明。 真实函数(f)（“Truth”）和预测函数（“Pred”）相差很大。

y_hat = torch.repeat_interleave(y_train.mean(), n_test)
plot_kernel_reg(y_hat)