文章目录
- 2014 年考研管理类联考数学真题
- 一、问题求解(本大题共 15 小题,每小题 3 分,共 45 分)下列每题给出 5 个选项中,只有一个是符合要求的,请在答题卡上将所选择的字母涂黑。
- 真题(2014-01)-应用题
- 真题(2014-02)
- 真题(2014-03)
- 真题(2014-04)
- 真题(2014-05)
- 真题(2014-06)-比例应用题-溶液浓度
- 真题(2014-07)-数列-等差数列
- 真题(2014-08)-应用题-路程
- 真题(2014-09)-数据分析
- 真题(2014-10)-算术-实数-质数
- 真题(2014-11)-几何-解析几何-圆方程
- 真题(2014-12)
- 真题(2014-13)-计数原理-组合
- 真题(2014-14)-几何-立体几何-球
- 真题(2014-15)
- 二.条件充分性判断:(第 16-25 小题,每小题 3 分,共 30 分)
- 真题(2014-16)-A-方程
- 真题(2014-17)-B-代数-不等式
- 真题(2014-18)-数列
- 真题(2014-19)-代数-分式
- 真题(2014-20)-A-几何-平面几何-圆
- 真题(2014-21)-A-方程-一元二次方程-判别式
- 真题(2014-22)-C-函数-一元二次函数
- 真题(2014-23)
- 真题(2014-24)-C-数据描述-平均值&方差
- 真题(2014-25)-A-代数-不等式
2014 年考研管理类联考数学真题
一、问题求解(本大题共 15 小题,每小题 3 分,共 45 分)下列每题给出 5 个选项中,只有一个是符合要求的,请在答题卡上将所选择的字母涂黑。
真题(2014-01)-应用题
1.某部门在一次联欢活动中共设了 26 个奖,奖品均价为 280 元,其中一等奖单价为 400 元, 其他奖品均价为 270 元,则一等奖的个数为( )
A.6
B.5
C.4
D.3
E.2

真题(2014-02)
2.某单位进行办公室装修,若甲、乙两个装修公司合作,需 10 周完成,工时费为 100 万元;甲公司单独做 6 周后由乙公司接着做 18 周完成,工时费为 96 万元.则甲公司每周的工时费为( )
A.7.5 万元
B.7 万元
C.6.5 万元
D.6 万元
E.5.5 万元

真题(2014-03)
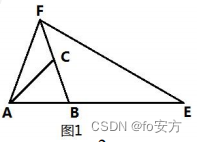
3.如图 1,已知 AE = 3AB,BF = 2BC,若△ABC 的面积是 2,则△AEF 的面积为( )
A.14
B.12
C.10
D.8
E.6

真题(2014-04)
4.某公司投资一个项目。已知上半年完成了预算的
1
3
\frac{1}{3}
31 ,下半年完成了剩余部分的
2
3
\frac{2}{3}
32 ,此时还有 8 千万元投资未完成,则该项目的预算为( )
A.3 亿元
B.3.6 亿元
C.3.9 亿元
D.4.5 亿元
E.5.1 亿元

真题(2014-05)
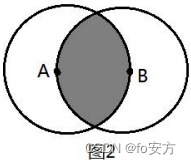
5.如图 2 所示,圆 A 与圆 B 的半径均为 1,则阴影部分的面积为( )
A.
2
π
3
\frac{2π}{3}
32π
B.
3
2
\frac{\sqrt{3}}{2}
23
C.
π
3
−
3
4
\frac{π}{3}-\frac{\sqrt{3}}{4}
3π−43
D.
2
π
3
−
3
4
\frac{2π}{3}-\frac{\sqrt{3}}{4}
32π−43
E.
2
π
3
−
3
2
\frac{2π}{3}-\frac{\sqrt{3}}{2}
32π−23
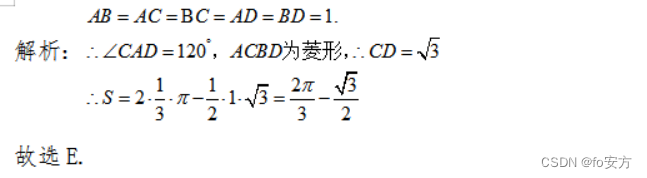
真题(2014-06)-比例应用题-溶液浓度
6.某容器中装满了浓度为 90%的酒精,倒出 1 升后用水将容器注满,搅拌均匀后又倒出 1升,再用水将容器注满,已知此时的酒精浓度为 40%,则该容器的容积是( )
A.2.5 升
B.3 升
C.3.5 升
D.4 升
E.4.5 升

真题(2014-07)-数列-等差数列
7.已知{
a
n
a_n
an}为等差数列,且
a
2
−
a
5
+
a
8
=
9
a_2-a_5+a_8=9
a2−a5+a8=9 ,则
a
1
+
a
2
+
.
.
.
+
a
9
=
()
a_1+a_2+...+a_9=( )
a1+a2+...+a9=()
A.27
B.45
C.54
D.81
E.182
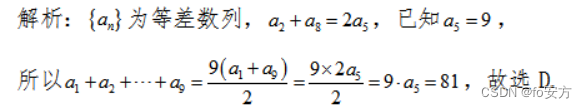
真题(2014-08)-应用题-路程
8.甲、乙两人上午 8:00 分别自 A,B 两地出发相向而行,9:00 第一次相遇,之后速度均提高了 1.5 公里/小时,甲到 B 地、乙到 A 地后都立刻沿原路返回.若两人在 10:30 第二次相遇,则 A、B 两地的距离为( )
A.5.6 公里
B.7 公里
C.8 公里
D.9 公里
E.9.5 公里

真题(2014-09)-数据分析
9.掷一枚均匀的硬币若干次,当正面向上次数大于反面向上次数时停止,则在 4 次之内停止的概率为( )
A.
1
8
\frac{1}{8}
81
B.
3
8
\frac{3}{8}
83
C.
5
8
\frac{5}{8}
85
D.
3
16
\frac{3}{16}
163
E.
5
16
\frac{5}{16}
165

真题(2014-10)-算术-实数-质数
10.若几个质数(素数)的乘积为 770,则它们的和为( )
A.85
B.84
C.28
D.26
E.25
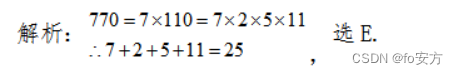
真题(2014-11)-几何-解析几何-圆方程
11.已知直线
l
l
l是圆
x
2
+
y
2
=
5
x^2+y^2=5
x2+y2=5在点(1,2)处的切线,则
l
l
l在 y 轴上的截距为( )
A.
2
5
\frac{2}{5}
52
B.
2
3
\frac{2}{3}
32
C.
3
2
\frac{3}{2}
23
D.
5
2
\frac{5}{2}
25
E.5

真题(2014-12)
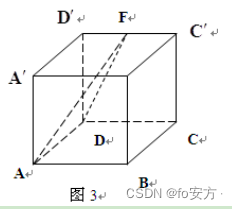
12.如图 3,正方体
A
B
C
D
−
A
′
B
′
C
′
D
′
ABCD-A'B'C'D'
ABCD−A′B′C′D′的棱长为 2, F 是棱
C
′
D
′
C'D'
C′D′的中点,则 AF 的长( )
A.3
B.5
C.
5
\sqrt{5}
5
D. 2
2
\sqrt{2}
2
E. 2
3
\sqrt{3}
3
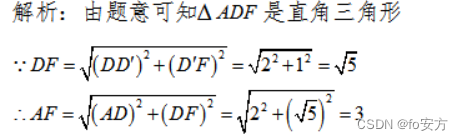
真题(2014-13)-计数原理-组合
13.某项活动中,将 3 男 3 女 6 名志愿者随机地分成甲、乙、丙三组,每组 2 人,则每组志愿者都是异性的概率为( )
A.
1
90
\frac{1}{90}
901
B.
1
15
\frac{1}{15}
151
C.
1
10
\frac{1}{10}
101
D.
1
5
\frac{1}{5}
51
E.
2
5
\frac{2}{5}
52

真题(2014-14)-几何-立体几何-球
14.某工厂在半径为 5cm 的球形工艺品上镀一层装饰金属,厚度为 0.01cm.已知装饰金属的原材料是棱长为 20cm 的正方体锭子,则加工 10 000 个该工艺品需要的锭子数量最少为(不考虑加工损耗,π ≈ 3.14 )( )
A.2
B.3
C.4
D.5
E.20

真题(2014-15)
15.某单位决定对 4 个部门的经理进行轮岗,要求每位经理必须轮换到 4 个部门中的其他部门任职,则不同的轮岗方案有( )
A.3 种
B.6 种
C.8 种
D.9 种
E.10 种
二.条件充分性判断:(第 16-25 小题,每小题 3 分,共 30 分)
要求判断每题给出的条件(1)和(2)能否充分支持题干所陈述的结论,A、B、C、D、 E 五个选项为判断结果,请选择一项符合试题要求的判断,请在答题卡上将所选的字母涂黑。
(A)条件(1)充分,但条件(2)不充分
(B)条件(2)充分,但条件(1)不充分
(C)条件(1)和(2)都不充分,但联合起来充分
(D)条件(1)充分,条件(2)也充分
(E)条件(1)不充分,条件(2)也不充分,联合起来仍不充分
真题(2014-16)-A-方程
16.已知曲线l :
y
=
a
+
b
x
−
6
x
2
+
x
3
y=a+bx-6x^2+x^3
y=a+bx−6x2+x3,则
(
a
+
b
−
5
)
(
a
−
b
−
5
)
=
0
(a+b-5)(a-b-5)=0
(a+b−5)(a−b−5)=0 .
(1)曲线l 过点(1,0) (2)曲线l 过点(-1,0)

真题(2014-17)-B-代数-不等式
17.不等式
∣
x
2
+
2
x
+
a
∣
≤
1
|x^2+2x+a|≤1
∣x2+2x+a∣≤1的解集为空集.
(1) a < 1
(2) a > 2

方法二:见“
x
2
x^2
x2”首选配平方。
∣
x
2
+
2
x
+
1
+
a
−
1
∣
≤
1
|x^2+2x+1+a-1|≤1
∣x2+2x+1+a−1∣≤1,得:
∣
(
x
+
1
)
2
+
∣
a
−
1
∣
∣
>
1
|(x+1)^2+|a-1||>1
∣(x+1)2+∣a−1∣∣>1,得:
(
x
+
1
)
2
≥
0
(x+1)^2≥0
(x+1)2≥0,
a
−
1
>
1
a-1>1
a−1>1得:
a
−
1
>
1
a-1>1
a−1>1,得:
a
>
2
a>2
a>2。
真题(2014-18)-数列
18.甲、乙、丙三人的年龄相同
(1)甲、乙、丙的年龄成等差数列
(2)甲、乙、丙的年龄成等比数列

真题(2014-19)-代数-分式
19.设 x 是非零实数,则
x
3
+
1
x
3
=
18
x^3+\frac{1}{x^3}=18
x3+x31=18
(1)
x
+
1
x
=
3
x+\frac{1}{x}=3
x+x1=3
(2)
x
2
+
1
x
2
=
7
x^2+\frac{1}{x^2}=7
x2+x21=7

真题(2014-20)-A-几何-平面几何-圆
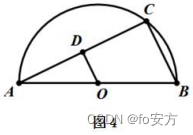
20.如图 4 所示, O 是半圆的圆心, C 是半圆上的一点, OD ⊥ AC ,则能确定OD 的长.
(1)已知 BC 的长
(2)已知 AO 的长

真题(2014-21)-A-方程-一元二次方程-判别式
21.方程
x
2
+
2
(
a
+
b
)
x
+
c
2
=
0
x^2+2(a+b)x+c^2=0
x2+2(a+b)x+c2=0 有实根.
(1) a, b, c 是一个三角形的三边长
(2)实数a, b, c 成等差数列

真题(2014-22)-C-函数-一元二次函数
22.已知二次函数为
f
(
x
)
=
a
x
2
+
b
x
+
c
f(x)=ax^2+bx+c
f(x)=ax2+bx+c ,则能确定a, b, c 的值.
(1)曲线 y = f (x) 过点(0, 0) 和点(1,1)
(2)曲线 y = f (x) 与直线 y = a + b 相切

真题(2014-23)
23.已知袋中装有红、黑、白三种颜色的球若干个,则红球数量最多.
(1)随机取出的一球是白球的概率为
2
5
\frac{2}{5}
52
(2)随机取出的两球中至少有一个黑球的概率小于
1
5
\frac{1}{5}
51

真题(2014-24)-C-数据描述-平均值&方差
24.已知m={
a
,
b
,
c
,
d
,
e
a,b,c,d,e
a,b,c,d,e}是一个整数集合.则能确定集合m .
(1) a, b, c, d , e 的平均值为 10
(2) a, b, c, d , e 的方差为 2

真题(2014-25)-A-代数-不等式
25.已知 x, y 为实数,则
x
2
+
y
2
=
1
x^2+y^2=1
x2+y2=1.
(1)
4
y
−
3
x
≥
5
4y - 3x ≥ 5
4y−3x≥5
(2)
(
x
−
1
)
2
+
(
y
−
1
)
2
≥
5
(x-1)^2+(y-1)^2≥5
(x−1)2+(y−1)2≥5