Matlab通信仿真系列——离散信号和系统

news2024/11/16 23:45:29

微信公众号上线，搜索公众号小灰灰的FPGA,关注可获取相关源码，定期更新有关FPGA的项目以及开源项目源码，包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等
在这里插入图片描述
本节目录

一、离散信号
1、离散信号定义
2、抽样周期与抽样范围
3、信号相加、相乘、卷积和
二、离散时间系统
三、Matlab源码
(1)信号相加、相乘、卷积和源码
(2)离散时间系统源码

本节内容
一、离散信号
1、离散信号定义
通常一个信号x(t)可以用来表示连续时间信号(模拟信号)，也可以用来表示离散时间信号(数字信号)。
离散信号x(t),t表示在时间轴上的离散点上的取值，可以表示为nTs，其中Ts表示相邻两个点之间的时间间隔，也就是所谓的抽样周期，n取整数。
x(nTs)=-N1,…,-1,0,1…,N2,其中N1,N2是n的取值范围，Ts归一化为1，则x(nTs)=x(n)。
在上述关系式中，由于x(n)仅是整数n的函数，故我们将x(n)称为离散时间序列。
2、抽样周期与抽样范围
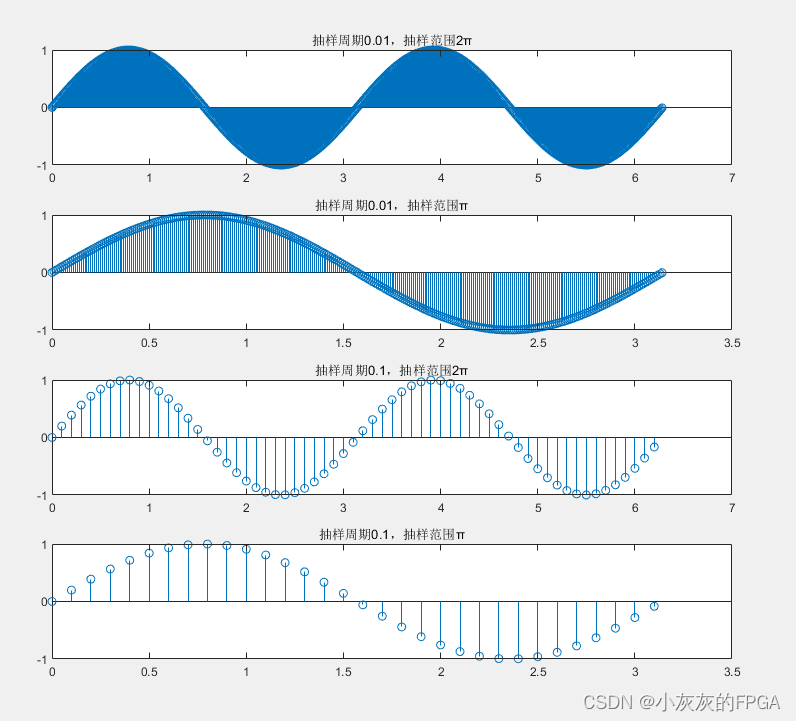
从图中可以看出抽样周期越小，对应的采样点越多，采样精度也就越高。
初学者注意：
stem(t1,x1)是以t1的数据为横坐标，x1的数据为纵坐标。

matlab代码示例：
一个正弦函数sin2t，
分别以0.01s和0.1s的抽样周期,
在π和2π范围抽样。

在这里插入图片描述

3、信号相加、相乘、卷积和
卷积和是求离散线性移不变系统输出响应的主要方法。
x(n)和h(n)的卷积和定义公式：
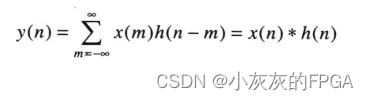
在这里插入图片描述
当序列n=0时，序列h(-m)是序列h(m)的时序取反的结果，时序取反使得h(m)以纵轴为中心翻转180°,相乘后求和的计算称为卷积和。
一般情况下，当x(n)及h(n)的离散序列长度分别为N1、N2时，卷积y(n)的长度则为N1+N2-1。
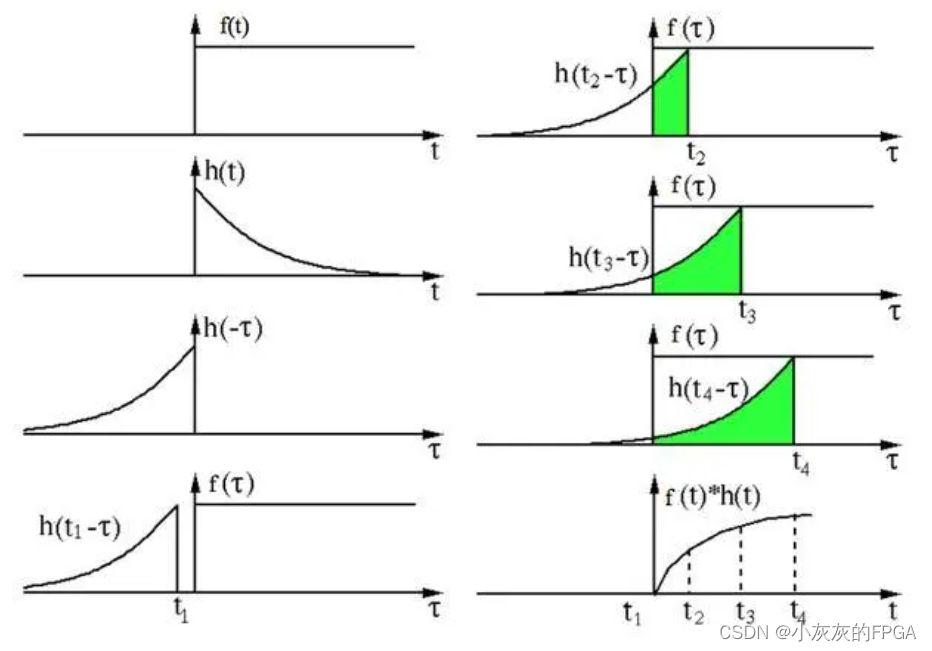
在这里插入图片描述
使用卷积和函数conv(x,y)可以求解两个序列的卷积和

matlab代码示例：
信号x1(n)=sin(2π×0.1n)
信号x2(n)=exp(-0.1n)
信号x3(n)=exp(-0.2n)
其中0≤n≤40
求x1(n)+x2(n);x1(n)×x2(n);x2(n)*x3(n)

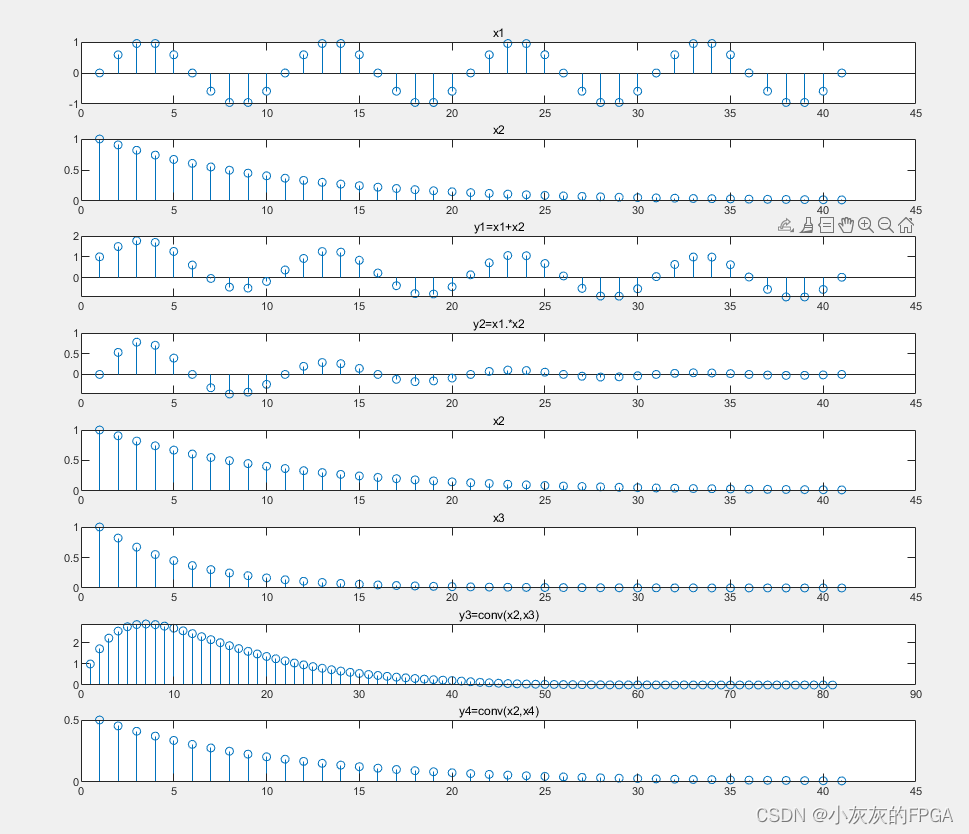
在这里插入图片描述

对于卷积和的理解，从y4=conv(x2,x4),可以看出来将x2关于y轴对称翻转，然后不断右移，与x4=1/2的交点构成面积为卷积和。
二、离散时间系统
一个离散时间系统，抽象看作一种变换或者一种映射，把输入序列x(n)变换为输出序列y(n),即y(n)=T[x(n)].
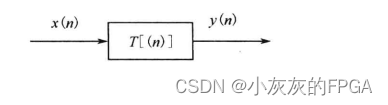
在这里插入图片描述

matlab代码示例：
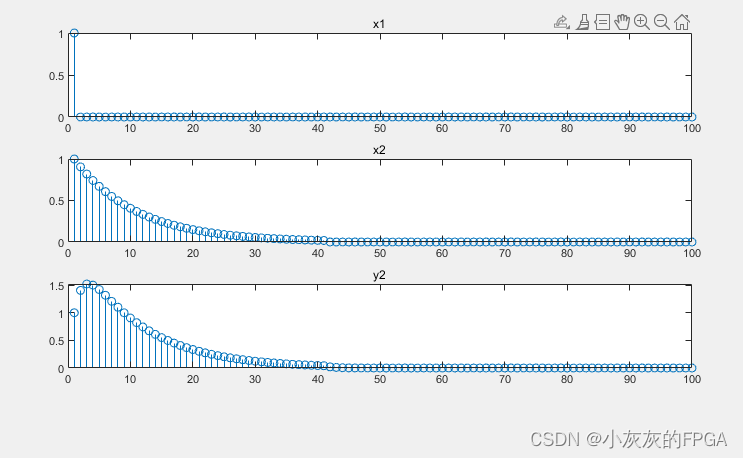
一个离散时间系统输入和输出关系为
y(n)=0.5y(n-1)+x(n)
不同输入激励x1和x2下的输出响应

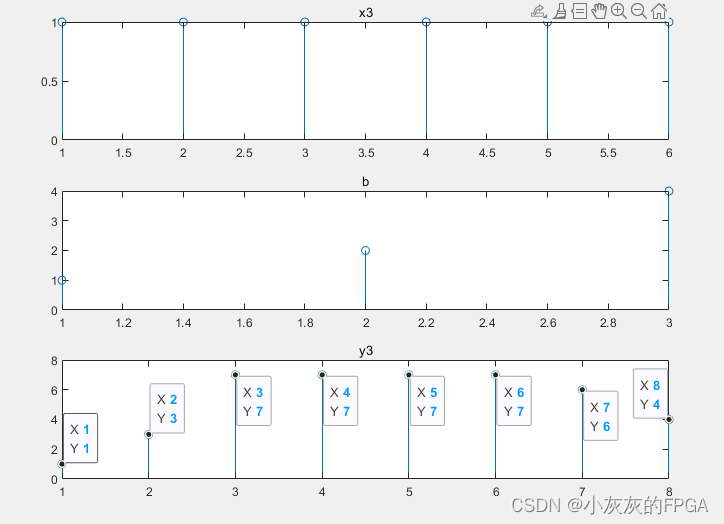
在这里插入图片描述

从上图Y可以看出来，卷积和的序列为1,3,7,7,7,7,6,4
有两种方式计算有限序列的卷积和，结果相比一致。
在这里插入图片描述

三、Matlab源码
(1)信号相加、相乘、卷积和源码

clear all;
n=0:40;             %离散序列的抽样范围
x1=sin(2*pi*0.1*n);
x2=exp(-0.1*n);
x3=exp(-0.2*n);
x4=1/2;
y1=x1+x2;           
y2=x1.*x2;          %x1与x2相乘，“.*”表示点乘
y3=conv(x2,x3);     %x2与x3卷积和
y4=conv(x2,x4);     %x2与x4卷积和
subplot(8,1,1);
stem(x1);
title('x1');
subplot(8,1,2);
stem(x2);
title('x2');
subplot(8,1,3);
stem(y1);
title('y1=x1+x2');
subplot(8,1,4);
stem(y2);
title('y2=x1.*x2');

subplot(8,1,5);
stem(x2);
title('x2');
subplot(8,1,6);
stem(x3);
title('x3');
subplot(8,1,7);
stem(y3);
title('y3=conv(x2,x3)');
subplot(8,1,8);
stem(y4);
title('y4=conv(x2,x4)');

(2)离散时间系统源码

clear all;
N=100;
x1=zeros(1,N);
x1(1)=1;
x2=zeros(1,N);
x2(1:41)=exp(-0.1*(0:40));
y1(1)=x1(1);
y2(1)=x2(1);
for n=2:N
    y1(n)=0.5*y1(n-1)+x1(n);
    y2(n)=0.5*y2(n-1)+x2(n);
end
figure;
subplot(4,1,1);
stem(x1);
title('x1');
subplot(4,1,2);
stem(x2);
title('x2');
subplot(4,1,3);
stem(y1);
title('y1');
subplot(4,1,3);
stem(y2);
title('y2');
figure;
x3=ones(1,6);
b=[1,2,4]
y3=conv(x3,b);
subplot(3,1,1);
stem(x3);
title('x3');
subplot(3,1,2);
stem(b);
title('b');
subplot(3,1,3);
stem(y3);
title('y3');