一.基本思想
设无向连通网为G=(V,E),令G的最小生成树为T=(U,TE),其初态为U=V,TE={},然后,按照边的权值由小到大的顺序,考察G的边集E中的各条边。若被考察的边的两个顶点属于T的两个不同的连通分量,则将此边作为最小生成树的边加入到T中,同时把两个连通分量连接为一个连通分量;若被考察边的两个顶点属于同一个连通分量,则舍去此边,以免造成回路,如此下去,当T中的连通分量个数为1时,此连通分量便为G的一棵最小生成树。
二.两种最小生成树算法比较
Prim算法:
对点做操作,维护一个在最小生成树中的点的顶点集U,以及一个待处理点的顶点集V-U,每次找出链接这两个集合的最短边,构成最小生成树,并将顶点加入集合U,知道所有顶点都处理完毕。
Kruskal算法:
对边做操作,每次选出一条最短边,如果它和当前最小生成树不构成回路就将其加入最小生成树,否则将其删除,知道所有边都处理完毕。
三.克鲁斯卡尔算法的伪代码描述
1.初始化
U=V;TE={}
2.重复下述操作直到T中的连通分量个数为1
2.1 在E中寻找最短边(u,v);
2.2 如果顶点u,v位于T的两个不同连通分量,则
2.2.1 将边(u,v)并入TE;
2.2.2 将这两个连通分量合为一个;
2.3 标记边(u,v),使得(u,v)不参加后续最短边的选取
关键:如何判别被考察边的两个顶点是否位于两个连通分量
四.Kruskal算法需要解决的问题
1.图用哪种存储结构更合适?
如果采用邻接矩阵或者邻接表则需要搜索所有的边才能找到最短边
需要改进
2.边的排序问题
插入排序 O(n^2)
堆排序/快速排序 O(elog2e)
3.如何判别被考察边的两个顶点是否位于两个连通分量?
所属的树是否有相同的根节点。
五.数据结构的设计
1.图的存储结构
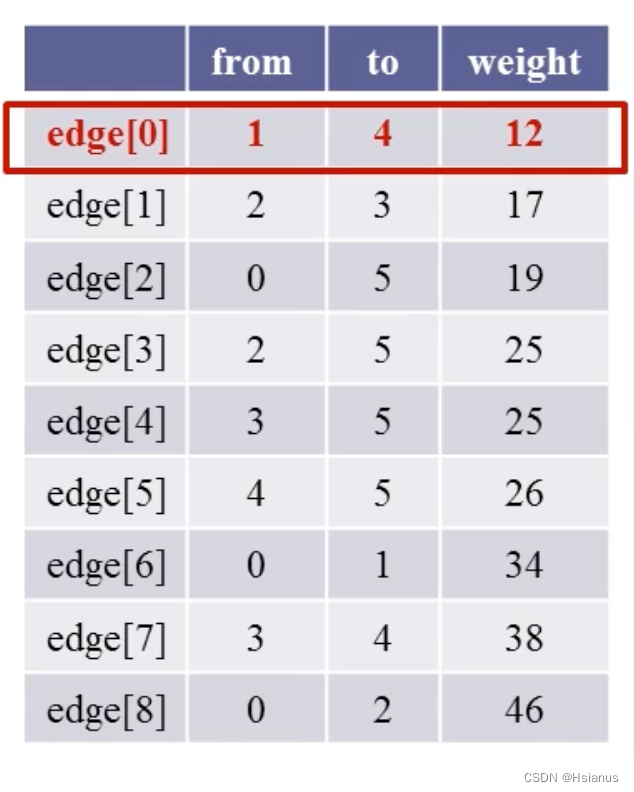
因为Kruskal算法是依次对图中的边进行操作,因此考虑边集数组存储图中的边,为了提高查找速度,将边集数组按边上的权排序。
const int MaxEdge=100;
struct EdgeType{
int from,to;//边依附的两个顶点
int weight;//边上的权值
};
template <class T>
struct EdgeGraph{
T vertex[MAX_VERTEX];//存放图顶点的数据
EdgeType edge[MaxEdge];//存放边的数组
int vertexNum,edgeNum;//图的顶点数和边数
};
2.连通分量
Kruskal算法实质上是使生成树以一种随意的方式生长,初始时,每个顶点构成一颗生成树。然后,每生长一次,就将两棵树合并,到最后合并成一棵树。
因此,可以设置一个数组parent[n],元素parent[i]表示顶点i的双亲结点,初始时,parent[i]=-1,表示顶点i没有双亲,即该结点是所在生成树的根节点;对于边(u,v),设vex1和vex2分别表示两个顶点所在树的根结点,如果vex1!=vex2,则顶点u和v必位于不同的连通分量,令parent[vex2]=vex1,实现将两棵树合并。
六.代码
template <class T>
void Kruskal(struct EdgeGraph<T> G){
int i,num=0,vex1,vex2;//num用来记录生成树的边的条数
int parent[G.vertexNum];
for(i=0;i<G.vertexNum;i++){
parent[i]=-1;//parent数组初始化
}
//对图G中的edge数组按照weight进行排序
quickSort(G.edge, 0, G.edgeNum-1);
for(i=0;i<G.edgeNum;i++){
vex1=findRoot(parent, G.edge[i].from);
vex2=findRoot(parent, G.edge[i].to);
if(vex1!=vex2){
outputMST(G.edge[i]);
parent[vex2]=vex1;//合并生成树
num++;
if(num==G.vertexNum-1){
return;
}
}
}
}
const int MaxEdge=100;
struct EdgeType{
int from,to;//边依附的两个顶点
int weight;//边上的权值
};
template <class T>
struct EdgeGraph{
T vertex[MAX_VERTEX];//存放图顶点的数据
EdgeType edge[MaxEdge];//存放边的数组
int vertexNum,edgeNum;//图的顶点数和边数
};
template <class T>
void Kruskal(struct EdgeGraph<T> G);
int findRoot(int parent[],int v){
int t=v;
while(parent[t]>-1){
t=parent[t];
}
return t;
}
int partition(EdgeType edge[],int first,int end);
void quickSort(EdgeType edge[],int first,int end);
void outputMST(EdgeType edge){
cout<<"("<<edge.from<<","<<edge.to<<")"<<edge.weight<<endl;
}