让我们首先概述一些影响普通梯度下降算法的问题。

1. 局部极小值

梯度下降可能会陷入局部最小值，即不是成本函数的全局最小值但仍低于周围点的点。当成本函数有多个谷值时，就会发生这种情况，并且算法陷入其中而不是达到全局最小值，如下所示：

所有图像均由作者创建

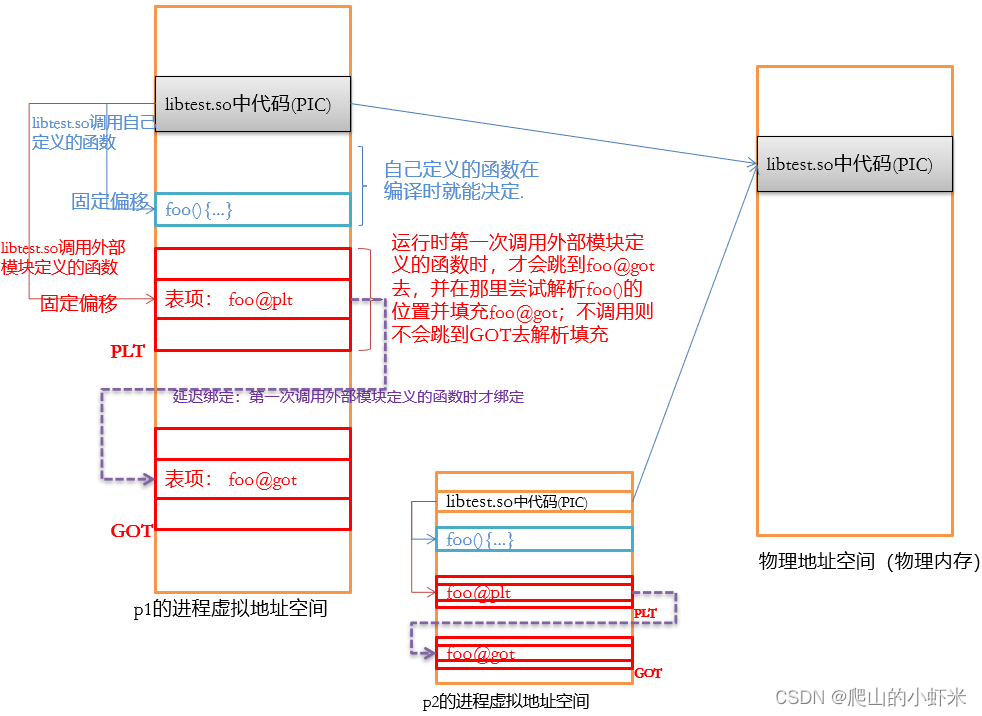
2. 鞍点

鞍点是成本函数中的一个点，其中一个维度具有比周围点更高的值，而另一个维度具有更低的值。梯度下降可能会在这些点上陷入困​​境，因为一个方向上的梯度指向较低的值，而另一个方向上的梯度则指向较高的值。

3. 高原期

平稳期是成本函数中梯度非常小或接近于零的区域。这可能会导致梯度下降需要很长时间或不收敛。

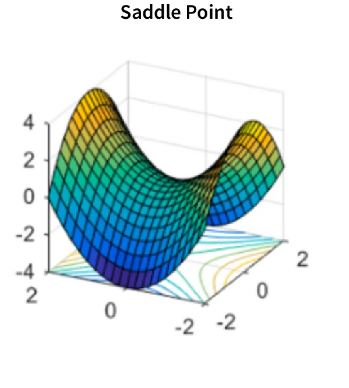
4. 振荡

当学习率太高时就会出现振荡，导致算法超过最小值并来回振荡。

梯度下降还面临其他一些困难，其中最值得注意和广泛讨论的是梯度消失和梯度爆炸。

三、基于动量的梯度下降如何工作

        在研究了梯度下降的问题以及提出增强和改进的动机之后，让我们继续讨论梯度下降的实际工作原理。这只需要一些基本的代数，并且会用简单的英语进行解释。

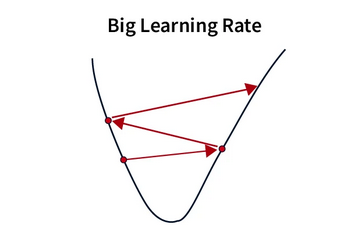
        常规梯度下降的基本表达式如下：

这里，w_t是当前时间步的权重，w_{t-1}是上一个时间步的权重，η是学习率，最后一项是损失函数相对于权重的偏导数上一步（又名渐变）。

现在，我们必须包含动量项并修改更新方程以考虑新的超参数和动量。

这里，V_t定义为：

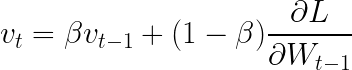
该方程称为指数加权平均值。β 是我们的动量超参数。当 β = 0 时，方程与普通梯度下降相同。

我们从 V_0 = 0 开始，并将方程更新为 t= 1…n。

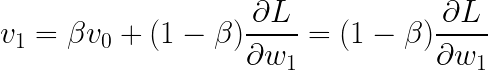
使用Codecog制作

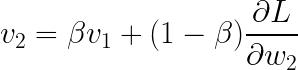
替换：

简化：

现在，

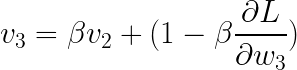
替换：

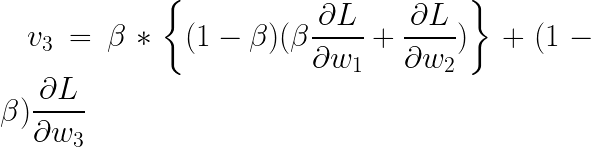
简化：

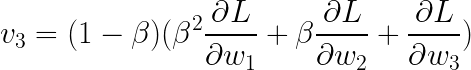
概括：

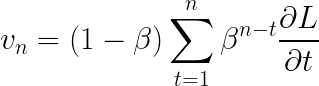
广义求和包括通过所有迭代建立的所有先前梯度。

四、超参数 Beta

现在的问题是我们将新的超参数 β 设置为什么。

如果我们将其设置为一个较低的值，例如0.1，那么t=3时的梯度将贡献其值的100%，t=2时的梯度将贡献其值的10%，而t=1时的梯度将仅贡献其值。贡献其价值的1%。您可以看到，如果我们将 β 设置得太低，早期梯度的贡献会迅速减少。

另一方面，如果我们为 β 设置一个较高的值，例如 0.9，则 t=3 时的梯度将贡献其值的 100%，t=2 时的梯度将贡献其值的 90%，而 t=3 时的梯度将贡献其值的 90%。 t=1将贡献其价值的81%。

我们得出的结论是，较高的 β 将包含更多来自过去的梯度。这就是动力的含义以及它如何在整个过程中建立起来。

五、使用 NumPy 在 Python 中实现

        这是带有动量的梯度下降的实现，以及与普通梯度下降的逐步解释和输出比较。在深入实现之前，我们先了解一下普通梯度下降和动量梯度下降之间的区别：

普通梯度下降：
1. 计算损失函数相对于参数的梯度。
2. 通过从当前参数值中减去梯度大小的一小部分（学习率）来更新参数。
3. 重复步骤 1 和 2，直到达到收敛。

带动量的梯度下降：
1. 计算损失函数相对于参数的梯度。
2. 计算步骤 1 中梯度的指数加权移动平均值（动量）。
3. 通过使用动量项修改普通梯度下降中的更新步骤来更新参数。
4. 重复步骤 1-3，直至达到收敛。

现在，我们来看看实现过程：

import numpy as np

def gradient_descent_momentum(X, y, learning_rate=0.01, momentum=0.9, num_iterations=100):
    # Initialize the parameters
    num_samples, num_features = X.shape
    theta = np.zeros(num_features)
    
    # Initialize the velocity vector
    velocity = np.zeros_like(theta)
    
    # Perform iterations
    for iteration in range(num_iterations):
        # Compute the predictions and errors
        predicted = np.dot(X, theta)
        errors = predicted - y
        
        # Compute the gradients
        gradients = (1/num_samples) * np.dot(X.T, errors)
        
        # Update the velocity
        velocity = momentum * velocity + learning_rate * gradients
        
        # Update the parameters
        theta -= velocity
        
        # Compute the mean squared error
        mse = np.mean(errors**2)
        
        # Print the MSE at each iteration
        print(f"Iteration {iteration+1}, MSE: {mse}")
    
    return theta
Now, let’s compare the output of Gradient Descent with Momentum to Vanilla Gradient Descent using a simple linear regression problem:

# Generate some random data
np.random.seed(42)
X = np.random.rand(100, 1)
y = 2 + 3 * X + np.random.randn(100, 1)

# Apply Gradient Descent with Momentum
theta_momentum = gradient_descent_momentum(X, y, learning_rate=0.1, momentum=0.9, num_iterations=100)

# Apply Vanilla Gradient Descent
theta_vanilla = gradient_descent(X, y, learning_rate=0.1, num_iterations=100)

        现在，让我们使用简单的线性回归问题将动量梯度下降与普通梯度下降的输出进行比较：

# Generate some random data
np.random.seed(42)
X = np.random.rand(100, 1)
y = 2 + 3 * X + np.random.randn(100, 1)

# Apply Gradient Descent with Momentum
theta_momentum = gradient_descent_momentum(X, y, learning_rate=0.1, momentum=0.9, num_iterations=100)

# Apply Vanilla Gradient Descent
theta_vanilla = gradient_descent(X, y, learning_rate=0.1, num_iterations=100)

输出：

Iteration 1, MSE: 5.894802675477298
Iteration 2, MSE: 4.981474209682729
Iteration 3, MSE: 4.543813739311503
...
Iteration 98, MSE: 0.639280357661573
Iteration 99, MSE: 0.6389711476228525
Iteration 100, MSE: 0.63867258334531

Iteration 1, MSE: 5.894802675477298
Iteration 2, MSE: 4.981474209682729
Iteration 3, MSE: 4.543813739311503
...
Iteration 98, MSE: 0.639280357661573
Iteration 99, MSE: 0.6389711476228525
Iteration 100, MSE: 0.63867258334531

正如我们从输出中看到的，动量梯度下降和普通梯度下降都提供了相似的结果。然而，由于动量项，动量梯度下降可以更快地收敛，这加速了最新梯度方向的更新，从而导致更快的收敛。

六、应用领域

        动量在机器学习社区中广泛用于优化非凸函数，例如深度神经网络。根据经验，动量方法优于传统的随机梯度下降方法。在深度学习中，SGD 广泛流行，是许多优化器（例如 Adam、Adadelta、RMSProp 等）的底层基础，这些优化器已经利用动量来降低计算速度

        优化算法的动量扩展可在许多流行的机器学习框架中使用，例如 PyTorch、张量流和 scikit-learn。一般来说，任何可以用随机梯度下降解决的问题都可以从动量的应用中受益。这些通常是无约束的优化问题。可以应用动量的一些常见 SGD 应用包括岭回归、逻辑回归和支持向量机。当实施动量时，包括与癌症诊断和图像确定相关的分类问题也可以减少运行时间。就医疗诊断而言，计算速度的提高可以通过神经网络内更快的诊断时间和更高的诊断准确性直接使患者受益。

七、总结

        动量通过减少振荡效应并充当优化问题解决的加速器来改善梯度下降。此外，它还找到全局（而不仅仅是局部）最优值。由于这些优点，动量常用于机器学习，并通过 SGD 广泛应用于所有优化器。尽管动量的超参数必须谨慎选择，并且需要一些试验和错误，但它最终解决了梯度下降问题中的常见问题。随着深度学习的不断发展，动量应用将使模型和问题的训练和解决速度比没有的方法更快。

参考

Brownlee, J.（2021 年，10 月 11 日）。从头开始的梯度下降势头。掌握机器学习。Gradient Descent With Momentum from Scratch - MachineLearningMastery.com。

Sum，C.-S。Leung 和 K. Ho，“梯度下降学习的局限性”，发表于 IEEE Transactions on Neural Networks and Learning Systems，卷。31、没有。6，第 2227–2232 页，2020 年 6 月，doi：10.1109/TNNLS.2019.2927689 弗朗西斯科·佛朗哥

Srihari，S.（nd）。基本优化算法。深度学习。https://cedar.buffalo.edu/~srihari/CSE676/8.3%20BasicOptimizn.pdf