🤵‍♂️ 个人主页: @AI_magician
📡主页地址： 作者简介：CSDN内容合伙人，全栈领域优质创作者。
👨‍💻景愿：旨在于能和更多的热爱计算机的伙伴一起成长！！🐱‍🏍
🙋‍♂️声明：本人目前大学就读于大二，研究兴趣方向人工智能&硬件（虽然硬件还没开始玩，但一直很感兴趣！希望大佬带带）

【深度学习 | 核心概念】那些深度学习路上必经的核心概念，确定不来看看？ （一） 作者： 计算机魔术师 版本： 1.0 （ 2023.8.27 ）

---

摘要： 本系列旨在普及那些深度学习路上必经的核心概念，文章内容都是博主用心学习收集所写，欢迎大家三联支持！本系列会一直更新，核心概念系列会一直更新！欢迎大家订阅

该文章收录专栏
[✨— 《深入解析机器学习：从原理到应用的全面指南》 —✨]

白噪声检验

白噪声序列是一种在统计学和信号处理中常见的随机过程。它具有一些特定的特性，使其在各个频率上具有均匀的能量分布。由一系列相互独立、具有相同概率分布的随机变量组成的。这些随机变量之间没有任何相关性，因此在时间上是完全不相关的。这意味着序列中的每个值都是独立地从相同的概率分布中生成的。

其名称来源于光学中的类比。在光学中，白光是由各种频率的光波混合而成的，这些光波具有均匀的能量分布。类似地，白噪声序列在频率域上具有均匀的能量分布，从低频到高频都有相似的能量。

白噪声序列在许多领域中都有应用，包括信号处理、通信系统、金融市场建模等。它常被用作基准参考，用于比较其他信号或系统的性能。此外，白噪声序列还用于测试和校准设备，以及进行随机性分析和模拟实验。

在时间序列中，白噪声检验除了用于在预测前判断平稳序列是否随机外，还能有哪些用法呢？

-- 检验残差是否为白噪声，判断模型拟合的是否足够好，是否还存在有价值的信息待提取。

\1. 残差为白噪声，说明模型拟合的很好，残差部分为无法捕捉的纯随机数据。
\2. 残差非白噪声，说明模型哪里出了问题，比如参数没调好，需要继续优化；若如何优化模型也无法使得残差为白噪声，换模型或者集成模型，或者对残差进行二次预测。

白噪声的定义很简单，只要满足以下3个条件即可：
\1) E(εt)=μ
\2) Var(εt)=σ2
\3) Cov(εt,εs)=0,t≠s
另外一种常见的定义方式为一个具有零均值同方差的独立同分布的序列为白噪声。

白噪声检验方法常用有以下3种方法（自相关图、Box-Pierce检验、Ljung-Box检验），其中Ljung-Box检验相对用的多一些，在调用statsmodels库的acf函数计算自相关系数时，指定qstat=True，会同时返回对应滞后期数下的Ljung-Box检验结果。

自相关图

由定义知，白噪声完全无自相关性，除0阶自相关系数为1外，理想情况下∀k,(k>0) ，延迟k阶的样本自相关系数均为0。实际上由于样本序列的有限性，延迟k阶自相关系数并不完全为0，只要在0值附近即认为无自相关性。

由于随机扰动的存在，自相关系数并不严格等于0，我们期望在95%的置信度下，即相关系数均在 ±2/T 之间。如果一个序列中有较多自相关系数的值在边界之外，那么该序列很可能不是白噪声序列。上图中自相关系数均在边界之内，为白噪声序列。

Ljung-Box检验

实际应用中人们发现 Q 统计量在大样本场合( n 很大的场合)检验效果很好（传统检验方法中样本量大于30即认为大样本量，Joel等人指出当样本量在500这个量级时 Q 统计量检验效果较好），但是在小样本场合不太精确。为了弥补这一缺陷，Box和Ljung于1979年对其进行了改进，推导出LB(Ljung-Box)统计量。

假设条件：

• H0:ρ1=ρ2=…=ρm=0 （滞后m阶序列值之间相互独立，序列为独立同分布的白噪声）
• H1:∃ρk≠0$,1<=k<=m （滞后 m 阶序列值之间有相关性，序列为非独立同分布的白噪声）
  其中， ρk 为延迟k阶的自相关系数， m 为最大延迟阶数。

检验统计量： $Q_{LB}=n(n+2){\sum }_{k=1}^m{\rho }_k^2/n-k$

LB统计量同样近似服从自由度为 m 的 χ2 分布。其中， n 为序列观察期数， m 为指定的最大延迟阶数， ρ^__k 为延迟 k 阶自相关系数的估计值。

由于LB统计量就是Box和Pierce的Q统计量的修正，所以人们习惯把它们统称为Q统计量。

判断准则：

LB统计量小于选定置信水平下的临界值，或者 p 值大于显著性水平（如0.05），不能拒绝原假设，序列为白噪声；

LB统计量大于选定置信水平下的临界值，或者 p 值小于显著性水平（如0.05），拒绝原假设，序列非白噪声；

实践环节：

序列检验

import numpy as np
import matplotlib.pyplot as plt
from statsmodels.stats.diagnostic import acorr_ljungbox

np.random.seed(123)
# 白噪音
white_noise=np.random.standard_normal(size=100)

# 不再指定boxpierce参数，近返回QLB统计量检验结果
# 同时设置lags参数为一个列表，相应只返回对应延迟阶数的检验结果
res = acorr_ljungbox(white_noise, lags=[6,12,24,48], return_df=True)
print(res)

延迟6阶、12阶时 p值较大，增加到延迟24阶时，p值略小但也大于0.05，所以在95%的置信水平下认为序列为白噪声。（这部分则是随机序列的偶然因素了）

还有一种实现Ljung-Box检验的方式为，调用statsmodels包中的acf函数，计算自相关系数时指定qstat为True，表示返回结果中除返回自相关系数外，另返回自相关系数的独立性检验结果 QLB 统计量及对应 p 值。

import numpy as np
import pandas as pd
import statsmodels as sm

np.random.seed(123)
white_noise=np.random.standard_normal(size=100)

r, q, p = sm.tsa.stattools.acf(white_noise, nlags=12, qstat=True) # 额外返回q p 统计量
df = pd.DataFrame(zip(range(1,41), q, p), columns=['lag', 'lb_stat', 'lb_pvalue'])
print(df)

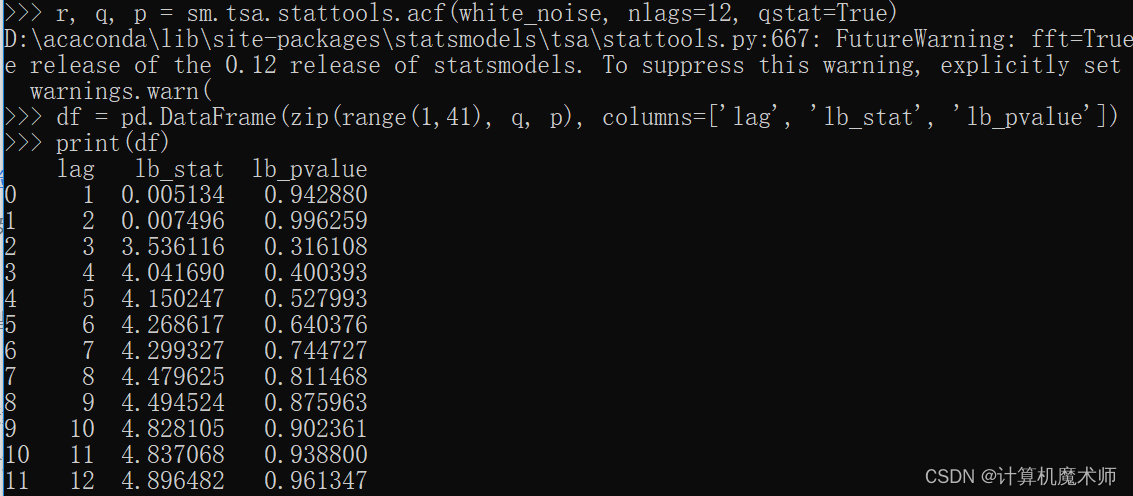
举一个为非白噪声的例子（太阳黑子）

import matplotlib.pyplot as plt
import statsmodels.api as sm
data = sm.datasets.sunspots.load_pandas().data
data = data.set_index('YEAR')

res = acorr_ljungbox(data.SUNACTIVITY, lags=[6,12,24], boxpierce=True, return_df=True)
print(res)

data.plot(figsize=(12, 4))
plt.show()

在这里插入图片描述

显而易见的数据有着周期性。

模型效果检验

而在检验模型效果的应用中，假设我们有一个时间序列数据如下：

[1.2, 2.4, 3.1, 4.6, 5.3, 6.8, 7.5, 8.9, 9.7, 10.2]

我们可以使用ARIMA模型对该数据进行拟合，并得到残差序列。然后，我们可以进行Ljung-Box白噪声检验来判断残差序列是否存在自相关。

import numpy as np
from statsmodels.tsa.arima_model import ARIMA
from statsmodels.stats.diagnostic import acorr_ljungbox

# 原始数据
data = np.array([1.2, 2.4, 3.1, 4.6, 5.3, 6.8, 7.5, 8.9, 9.7, 10.2])

# 拟合ARIMA模型，得到残差序列
model = ARIMA(data, order=(1, 0, 0))  # 这里以ARIMA(1, 0, 0)为例
model_fit = model.fit(disp=0)
residuals = model_fit.resid # 训练数据中的残差

# 进行Ljung-Box白噪声检验
lbvalue, pvalue = acorr_ljungbox(residuals, lags=5)  # 检验前5个滞后期

# 打印检验结果
print("Ljung-Box白噪声检验结果：")
for lag, p in enumerate(pvalue):
    print(f"滞后期{lag+1}：p-value={p}")

运行以上代码，我们可以得到如下的检验结果：

Ljung-Box白噪声检验结果：
滞后期1：p-value=0.8811740567913574
滞后期2：p-value=0.9395957812016121
滞后期3：p-value=0.9444992061584102
滞后期4：p-value=0.9826682340484362
滞后期5：p-value=0.9658631275329448

在这个案例中，我们可以看到每个滞后期的p-value都远大于0.05，意味着残差序列在这些滞后期上没有显著的自相关。因此，我们可以认为残差序列是一个白噪声序列，即没有自相关（模型效果优秀）。

参考文章：

https://zhuanlan.zhihu.com/p/430365631

						  🤞到这里，如果还有什么疑问🤞
					🎩欢迎私信博主问题哦，博主会尽自己能力为你解答疑惑的！🎩
					 	 🥳如果对你有帮助，你的赞是对博主最大的支持！！🥳