对于麻雀搜索算法的介绍,网上已经有不少资料了,这边公布SSA的matlab实现
下面展示SSA算法的核心代码以及详细注解
% 麻雀搜索算法函数定义
% 输入:种群大小(pop),最大迭代次数(Max_iter),搜索空间下界(lb),搜索空间上界(ub),问题维度(dim),目标函数(fobj)
% 输出:最优适应度值(Best_score),最优位置(Best_pos),每次迭代的最优适应度值(curve)
function [Best_score,Best_pos,curve]=SSA(pop,Max_iter,lb,ub,dim,fobj)
% 预警值
ST = 0.7;
% 发现者的比例
PD = 0.4;
% 意识到有危险麻雀的比重
SD = 0.2;
% 计算发现者数量和意识到有危险麻雀数量
PDNumber = round(pop*PD);
SDNumber = round(SD*PD);
% 种群初始化
X0=initialization(pop,dim,ub,lb);
X = X0;
% 计算初始适应度值
fitness = zeros(1,pop);
for i = 1:pop
fitness(i) = fobj(X(i,:));
end
% 对适应度值进行升序排序,找到最优和最差的适应度值
[fitness, index]= sort(fitness);
BestF = fitness(1);
WorstF = fitness(end);
% 更新全局最优适应度值
GBestF = fitness(1);
% 根据适应度值的排序结果,重新排列种群中的麻雀
for i = 1:pop
X(i,:) = X0(index(i),:);
end
% 初始化记录每次迭代的最优适应度值的数组
curve=zeros(1,Max_iter);
% 记录全局最优位置
GBestX = X(1,:);
% 初始化新的种群位置
X_new = X;
% 迭代开始
for i = 1: Max_iter
disp(['第',num2str(i),'次迭代'])
BestF = fitness(1);
WorstF = fitness(end);
% 麻雀的行为更新
for j = 1:PDNumber
if(rand(1)<ST)
% 麻雀降低飞行高度以避免风险
X_new(j,:) = X(j,:).*exp(-j/(rand(1)*Max_iter));
else
% 麻雀在原有位置上添加随机扰动,以模拟发现者的搜索行为
X_new(j,:) = X(j,:) + randn()*ones(1,dim);
end
end
for j = PDNumber+1:pop
if(j>(pop - PDNumber)/2 + PDNumber)
% 麻雀向全局最优麻雀靠近,以模拟麻雀的跟随行为
X_new(j,:)= randn().*exp((X(end,:) - X(j,:))/j^2);
else
% 麻雀向局部最优麻雀靠近,以模拟麻雀的跟随行为
A = ones(1,dim);
for a = 1:dim
if(rand()>0.5)
A(a) = -1;
end
end
AA = A'*inv(A*A');
X_new(j,:)= X(1,:) + abs(X(j,:) - X(1,:)).*AA';
end
end
% 对于意识到有危险的麻雀,进行特殊的行为更新
Temp = randperm(pop);
SDchooseIndex = Temp(1:SDNumber);
for j = 1:SDNumber
if(fitness(SDchooseIndex(j))>BestF)
% 如果适应度值大于当前最优值,麻雀向全局最优麻雀靠近
X_new(SDchooseIndex(j),:) = X(1,:) + randn().*abs(X(SDchooseIndex(j),:) - X(1,:));
```matlab
elseif(fitness(SDchooseIndex(j))== BestF)
% 如果适应度值等于当前最优值,麻雀进行随机行为
K = 2*rand() -1;
X_new(SDchooseIndex(j),:) = X(SDchooseIndex(j),:) + K.*(abs( X(SDchooseIndex(j),:) - X(end,:))./(fitness(SDchooseIndex(j)) - fitness(end) + 10^-8));
end
end
% 边界控制,防止麻雀飞出搜索空间
for j = 1:pop
for a = 1: dim
if length(ub)>1
if(X_new(j,a)>ub(a))
X_new(j,a) =ub(a);
end
if(X_new(j,a)<lb(a))
X_new(j,a) =lb(a);
end
else
if(X_new(j,a)>ub)
X_new(j,a) =ub;
end
if(X_new(j,a)<lb)
X_new(j,a) =lb;
end
end
end
end
% 更新位置
for j=1:pop
fitness_new(j) = fobj(X_new(j,:));
end
for j = 1:pop
if(fitness_new(j) < GBestF)
% 更新全局最优适应度值和位置
GBestF = fitness_new(j);
GBestX = X_new(j,:);
end
end
X = X_new;
fitness = fitness_new;
% 根据新的适应度值,重新排序种群
[fitness, index]= sort(fitness);
BestF = fitness(1);
WorstF = fitness(end);
for j = 1:pop
X(j,:) = X(index(j),:);
end
% 记录当前迭代的最优适应度值
curve(i) = GBestF;
disp(['current iteration is: ',num2str(i), ', best fitness is: ', num2str(GBestF)])
end
% 返回全局最优位置和最优适应度值
Best_pos =GBestX;
Best_score = curve(end);
end
将SSA应用到BP神经网络优化上,优化结果图如下:
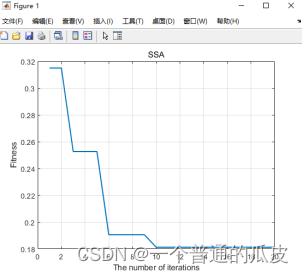
具体思路为:
1.清理环境:开始时,代码清理了MATLAB环境,关闭了所有图窗,清空了所有变量和命令行,以确保开始一个全新的会话。
2.导入数据:导入一个名为“数据集.xlsx”的Excel文件,并对数据进行了分析。数据集被分为训练集和测试集,其中80%的数据用作训练集。
3.数据归一化:为了使网络训练更有效,数据被归一化到0和1之间。
4.创建和配置神经网络:创建了一个新的前馈神经网络,其中隐藏层的节点数为15。然后,设置了网络的训练参数,包括训练次数、目标误差和学习率。
5.麻雀搜索算法(SSA)的应用:SSA是一种优化算法,用于寻找最优的权重和阀值以初始化神经网络。SSA模拟了麻雀的捕食行为,麻雀通过在搜索空间内搜索食物源来找到最优解。
6.网络训练和预测:用SSA找到的最优初始权重和阀值训练网络,并对训练集和测试集进行预测。
7.反归一化:预测完成后,数据被反归一化,以便可以与原始数据进行比较。
8.评估模型性能:计算了均方根误差(RMSE)、决定系数(R2)、均方误差(MSE)、剩余预测残差(RPD)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)来评估模型的性能。
9.结果可视化:最后,通过各种图形(包括预测结果、误差直方图、优化曲线、线性拟合图等)对结果进行了可视化。
完整的代码实现以及数据集见:
GitHub - dazhiwang233/matlab-implementation-of-SSA-BP-network: SSA-BP网络的matlab实现