目录

AdaBoost算法原理

AdaBoost工作详情

初始权重分配

第一轮

第二轮

后续轮次

最终模型

AdaBoost的API解释

AdaBoost 对房价进行预测

AdaBoost 与决策树模型的比较

结论

---

AdaBoost算法原理

在数据挖掘中，分类算法可以说是核心算法，其中 AdaBoost算法与随机森林算法一样都属于分类算法中的集成算法.

集成的含义就是集思广益，博取众长，当我们做决定的时候，我们先听取多个专家的意见，再做决定。集成算法通常有两种方式，分别是投票选举（bagging）和再学习（boosting）。 投票选举的场景类似把专家召集到一个会议桌前，当做一个决定的时候，让 K 个专家（K 个模 型）分别进行分类，然后选择出现次数最多的那个类作为最终的分类结果。再学习相当于把 K 个专家（K 个分类器）进行加权融合，形成一个新的超级专家（强分类器），让这个超级专家 做判断.

AdaBoost 的关键在于它会给训练数据中的每个样本分配一个权重，并在每一轮迭代中调整这些权重。错误分类的样本在下一轮迭代中会得到更高的权重，从而使弱分类器集中注意力于难以分类的样本。以下是一个具体的示例来解释 AdaBoost 算法的原理：

AdaBoost工作详情

假设我们有一个简单的二分类问题，训练数据集包含5个样本：{x1, x2, x3, x4, x5}，它们的真实标签分别为 {1, -1, 1, 1, -1}。

初始权重分配

首先，每个样本都被赋予相同的权重，即 1/5。

第一轮

1. 训练第一个弱分类器：例如，一个简单的决策树。
2. 计算错误率：弱分类器在加权训练数据上的错误率。例如，假设它错误地分类了样本 x2 和 x5。
3. 更新样本权重：增加被错误分类的样本的权重，减少正确分类的样本的权重。例如，x2 和 x5 的权重增加，而其余样本的权重减少。
4. 计算分类器权重：基于错误率计算分类器权重，错误率越低的分类器在最终模型中的权重越高。

第二轮

1. 训练第二个弱分类器：使用更新后的样本权重。
2. 重复计算错误率、更新样本权重和分类器权重的过程。

后续轮次

重复以上步骤，直到达到预定的迭代次数，或者达到某个性能阈值。

最终模型

最终的 AdaBoost 模型是所有弱分类器的加权组合，其中每个弱分类器的贡献由其权重决定。这样，模型在预测新数据时，会考虑所有弱分类器的预测并加权得到最终结果。

AdaBoost的API解释

AdaBoostClassifier(base_estimator=None, n_estimators=50, learning_rate=1.0, algorithm=’SAMME.R’, random_state=None)

这个函数，其中有几 个比较主要的参数，我分别来讲解下：

1. base_estimator：代表的是弱分类器。在 AdaBoost 的分类器和回归器中都有这个参数， 在 AdaBoost 中默认使用的是决策树，一般我们不需要修改这个参数，当然你也可以指定 具体的分类器。

2.   n_estimators：算法的最大迭代次数，也是分类器的个数，每一次迭代都会引入一个新的 弱分类器来增加原有的分类器的组合能力。默认是 50。

3.   learning_rate：代表学习率，取值在 0-1 之间，默认是 1.0。如果学习率较小，就需要比 较多的迭代次数才能收敛，也就是说学习率和迭代次数是有相关性的。当你调整 learning_rate 的时候，往往也需要调整 n_estimators 这个参数。

4.   algorithm：代表我们要采用哪种 boosting 算法，一共有两种选择：SAMME 和 SAMME.R。默认是 SAMME.R。这两者之间的区别在于对弱分类权重的计算方式不同。

5.   random_state：代表随机数种子的设置，默认是 None。随机种子是用来控制随机模式 的，当随机种子取了一个值，也就确定了一种随机规则，其他人取这个值可以得到同样的结果。如果不设置随机种子，每次得到的随机数也就不同

AdaBoost 对房价进行预测

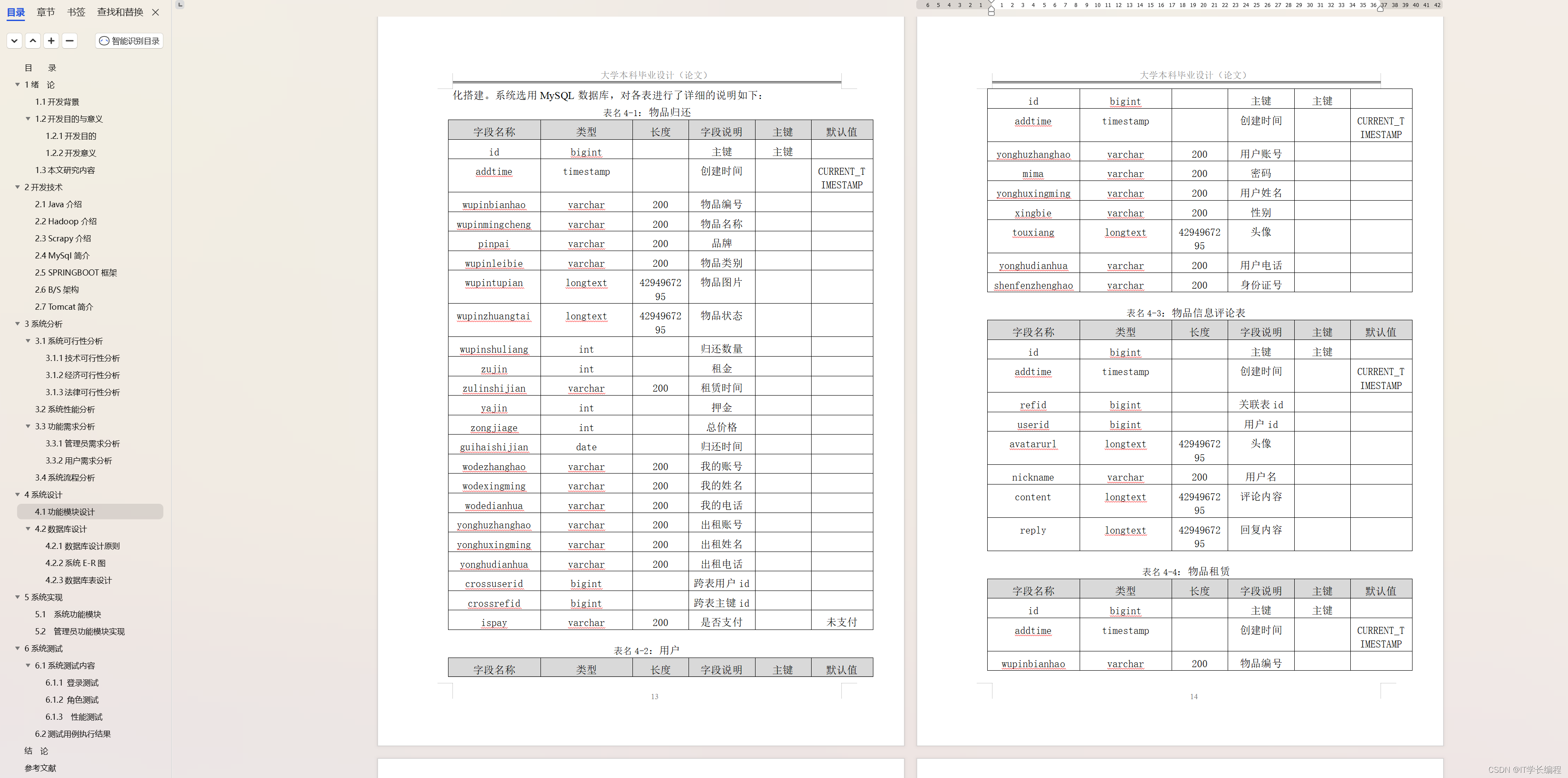
了解了 AdaBoost 工具包之后，我们看下 sklearn 中自带的波士顿房价数据集。这个数据集一共包括了 506 条房屋信息数据，每一条数据都包括了 13 个指标，以及一个房屋 价位。13 个指标的含义，可以参考下面的表格

这些指标分析得还是挺细的，但实际上，我们不用关心具体的含义，要做的就是如何通过这 13 个指标推导出最终的房价结果。
 
首先加载数据，将数据分割成训练集和测试集，然后创建 AdaBoost 回归模型，传入训练集 数据进行拟合，再传入测试集数据进行预测，就可以得到预测结果。最后将预测的结果与实际 结果进行对比，得到两者之间的误差。具体代码如下：

from sklearn.model_selection import train_test_split from sklearn.metrics import mean_squared_error from sklearn.datasets import load_boston
from sklearn.ensemble import AdaBoostRegressor
# 加载数据
data=load_boston()
# 分割数据
train_x, test_x, train_y, test_y = train_test_split(data.data, data.target, test_size=0.25, random_state=33)
# 使用AdaBoost回归模型
regressor=AdaBoostRegressor()

regressor.fit(train_x,train_y) 12 
pred_y = regressor.predict(test_x)

mse = mean_squared_error(test_y, pred_y)
print("房价预测结果  ", pred_y) 15 
print("均方误差  = ",round(mse,2))

同样，我们可以使用不同的回归分析模型分析这个数据集，比如使用决策树回归和 KNN 回归。
编写代码如下：

# 使用决策树回归模型
dec_regressor=DecisionTreeRegressor() dec_regressor.fit(train_x,train_y) 
pred_y = dec_regressor.predict(test_x) mse = mean_squared_error(test_y, pred_y)
print("决策树均方误差 = ",round(mse,2))

# 使用KNN回归模型
knn_regressor=KNeighborsRegressor()
knn_regressor.fit(train_x,train_y) 
pred_y = knn_regressor.predict(test_x) 
mse = mean_squared_error(test_y, pred_y)
print("KNN均方误差  = ",round(mse,2))

你能看到相比之下，AdaBoost 的均方误差更小，也就是结果更优。虽然 AdaBoost 使用了弱 分类器，但是通过 50 个甚至更多的弱分类器组合起来而形成的强分类器，在很多情况下结果 都优于其他算法。因此 AdaBoost 也是常用的分类和回归算法之一 

AdaBoost 与决策树模型的比较

在 sklearn 中 AdaBoost 默认采用的是决策树模型，我们可以随机生成一些数据，然后对比 下 AdaBoost 中的弱分类器（也就是决策树弱分类器）、决策树分类器和 AdaBoost 模型在 分类准确率上的表现。

如果想要随机生成数据，我们可以使用 sklearn 中的 make_hastie_10_2 函数生成二分类数 据。假设我们生成 12000 个数据，取前 2000 个作为测试集，其余作为训练集。有了数据和训练模型后，我们就可以编写代码。我设置了 AdaBoost 的迭代次数为 200，代 表 AdaBoost 由 200 个弱分类器组成。针对训练集，我们用三种模型分别进行训练，然后用测试集进行预测，并将三个分类器的错误率进行可视化对比，可以看到这三者之间的区别：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.metrics import zero_one_loss
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import  AdaBoostClassifier
# 设置AdaBoost迭代次数
n_estimators=200
# 使用
X,y=datasets.make_hastie_10_2(n_samples=12000,random_state=1)
# 从12000个数据中取前2000行作为测试集，其余作为训练集
train_x, train_y = X[2000:],y[2000:]
test_x, test_y = X[:2000],y[:2000]
# 弱分类器
dt_stump = DecisionTreeClassifier(max_depth=1,min_samples_leaf=1)
dt_stump.fit(train_x, train_y)
dt_stump_err = 1.0-dt_stump.score(test_x, test_y)
# 决策树分类器
dt = DecisionTreeClassifier()
dt.fit(train_x,  train_y)
dt_err = 1.0-dt.score(test_x, test_y)
# AdaBoost分类器
ada = AdaBoostClassifier(base_estimator=dt_stump,n_estimators=n_estimators)
ada.fit(train_x,  train_y)
# 三个分类器的错误率可视化
fig = plt.figure()
# 设置plt正确显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
ax = fig.add_subplot(111)
ax.plot([1,n_estimators],[dt_stump_err]*2, 'k-', label=u'决策树弱分类器 错误率')
ax.plot([1,n_estimators],[dt_err]*2,'k--', label=u'决策树模型 错误率')
ada_err = np.zeros((n_estimators,))
# 遍历每次迭代的结果 i为迭代次数, pred_y为预测结果
for i,pred_y in enumerate(ada.staged_predict(test_x)):
     # 统计错误率
    ada_err[i]=zero_one_loss(pred_y, test_y)
# 绘制每次迭代的AdaBoost错误率
ax.plot(np.arange(n_estimators)+1, ada_err, label='AdaBoost Test 错误率', color='orange')
ax.set_xlabel('迭代次数')
ax.set_ylabel('错误率')
leg=ax.legend(loc='upper right',fancybox=True)
plt.show()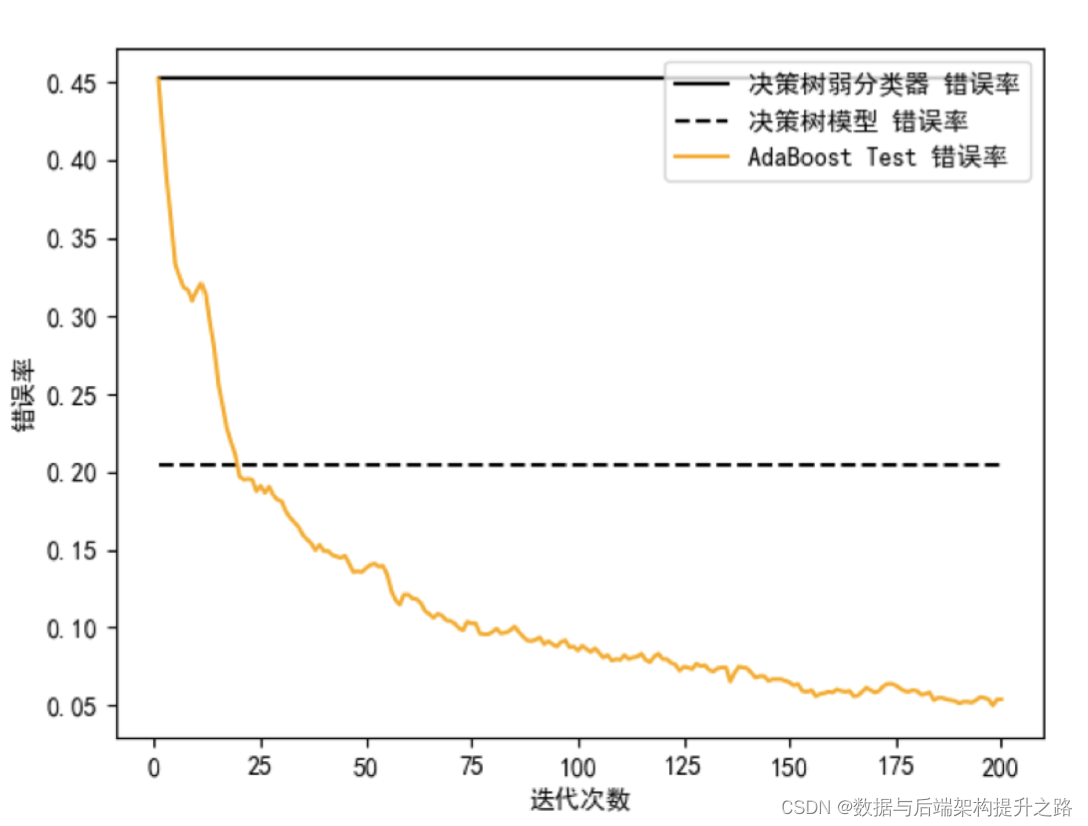

从图中你能看出来，弱分类器的错误率最高，只比随机分类结果略好，准确率稍微大于 50%。决策树模型的错误率明显要低很多。而 AdaBoost 模型在迭代次数超过 25 次之后，错 误率有了明显下降，经过 125 次迭代之后错误率的变化形势趋于平缓。

因此我们能看出，虽然单独的一个决策树弱分类器效果不好，但是多个决策树弱分类器组合起来形成的AdaBoost 分类器，分类效果要好于决策树模型。

结论

AdaBoost 算法有效地集中于那些难以正确分类的样本，逐渐调整分类器以解决这些难题。这使得 AdaBoost 成为一种强大的集成方法，尤其适用于处理复杂的分类问题。