题目

标题和出处

标题：具有所有最深结点的最小子树

出处：865. 具有所有最深结点的最小子树

难度

5 级

题目描述

要求

给定二叉树的根结点 $\text{root}$，每个结点的深度是该结点到根的最短距离。

返回包含原始树中所有最深结点的最小子树。

如果一个结点在整个树的所有结点中具有最大的深度，则该结点是最深的。

一个结点的子树是该结点加上它的所有后代的集合。

示例

示例 1：

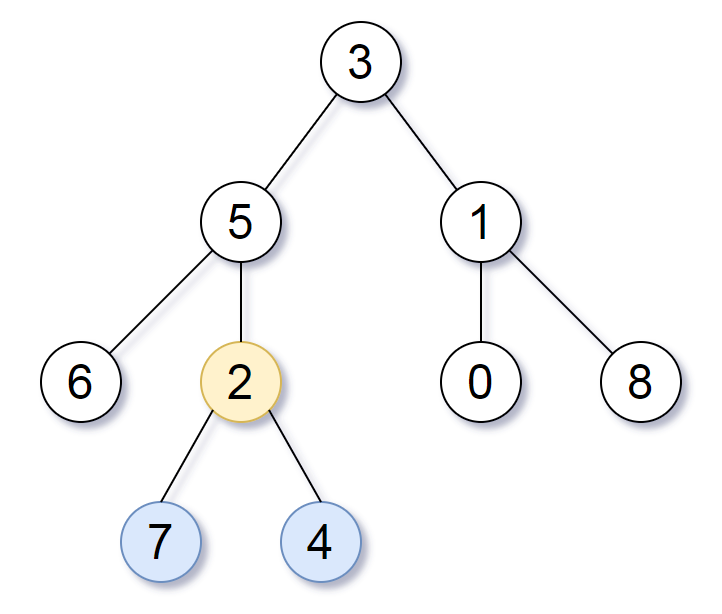
输入：$\text{root = [3,5,1,6,2,0,8,null,null,7,4]}$
输出：$\text{[2,7,4]}$
解释：
我们返回值为 $\text{2}$ 的结点，在图中用黄色标记。
在图中用蓝色标记的是树的最深的结点。
注意，结点 $\text{5}$、$\text{3}$ 和 $\text{2}$ 包含树中最深的结点，但结点 $\text{2}$ 的子树最小，因此我们返回它。

示例 2：

输入：$\text{root = [1]}$
输出：$\text{[1]}$
解释：根结点是树中最深的结点。

示例 3：

输入：$\text{root = [0,1,3,null,2]}$
输出：$\text{[2]}$
解释：树中最深的结点为 $\text{2}$，有效子树为结点 $\text{2}$、$\text{1}$ 和 $\text{0}$ 的子树，但结点 $\text{2}$ 的子树最小。

数据范围

• 树中结点数目在范围 $\text{[1, 500]}$ 内
• $\text{0}\le \text{Node.val}\le \text{500}$
• 树中的所有值各不相同

解法一

思路和算法

由于所有最深结点的深度相同，因此对于包含所有最深结点的子树，每个最深结点到子树根结点的距离相同。只要定位到所有最深结点，即可找到包含所有最深结点的最小子树的根结点。

为了定位到所有最深结点，可以使用层序遍历。从根结点开始依次遍历每一层的结点，在层序遍历的过程中需要区分不同结点所在的层，确保每一轮访问的结点为同一层的全部结点。遍历每一层结点之前首先得到当前层的结点数，即可确保每一轮访问的结点为同一层的全部结点。层序遍历访问的最后一层结点即为所有最深结点。

定位到所有最深结点之后，从最深结点向根结点移动，即每次从当前结点移动到父结点。由于每个最深结点到子树根结点的距离相同，因此每个最深结点将同时移动到包含所有最深结点的最小子树的根结点。使用哈希集合存储每次移动之后的结点集合，每次移动之后，结点数量一定不变或减少，当只剩下一个结点时，该结点即为包含所有最深结点的最小子树的根结点。

代码

class Solution {
    public TreeNode subtreeWithAllDeepest(TreeNode root) {
        Map<TreeNode, TreeNode> parentMap = new HashMap<TreeNode, TreeNode>();
        List<TreeNode> deepest = new ArrayList<TreeNode>();
        Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            deepest.clear();
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode node = queue.poll();
                deepest.add(node);
                TreeNode left = node.left, right = node.right;
                if (left != null) {
                    parentMap.put(left, node);
                    queue.offer(left);
                }
                if (right != null) {
                    parentMap.put(right, node);
                    queue.offer(right);
                }
            }
        }
        Set<TreeNode> nodes = new HashSet<TreeNode>(deepest);
        while (nodes.size() > 1) {
            Set<TreeNode> parents = new HashSet<TreeNode>();
            for (TreeNode node : nodes) {
                parents.add(parentMap.get(node));
            }
            nodes = parents;
        }
        return nodes.iterator().next();
    }
}

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是二叉树的结点数。层序遍历访问每个结点一次，需要 $O(n)$ 的时间，从所有最深结点移动到包含所有最深结点的最小子树的根结点的时间不超过 $O(n)$，因此总时间复杂度是 $O(n)$。

• 空间复杂度：$O(n)$，其中 $n$ 是二叉树的结点数。空间复杂度主要是队列空间和哈希集合，队列内元素个数不超过 $n$，哈希集合内元素个数不超过 $n$。

解法二

思路和算法

对于二叉树中的每个结点，考虑其左子树和右子树的深度。如果左子树和右子树的深度相同，则左子树和右子树中都有最深结点，当前结点就是包含所有最深结点的最小子树的根结点；如果左子树和右子树的深度不同，则所有最深结点一定在深度较大的子树中，需要在深度较大的子树中寻找包含所有最深结点的最小子树的根结点。因此，寻找包含所有最深结点的最小子树的根结点，等价于寻找左子树和右子树的深度相同的结点，以下将该结点称为「目标结点」。

从根结点开始深度优先搜索，计算每个子树的深度，并寻找目标结点。定义空树的深度为 $0$，当子树非空时，子树的深度为左子树的深度和右子树的深度中的最大值加 $1$。

寻找目标结点的具体做法如下。

1. 如果当前结点的左子树的深度和右子树的深度相同，则当前结点即为目标结点，当前子树的深度为左子树的深度加 $1$。

2. 否则，在深度较大的子树中寻找目标结点，当前子树的深度为深度较大的子树的深度加 $1$。

上述过程是一个递归的过程，递归的终止条件是当前结点为空或者当前结点的左子树的深度和右子树的深度相同，其余情况则调用递归。

对于每个结点，首先访问其子结点寻找目标结点和计算子树高度，然后根据访问子结点的结果得到当前结点的结果。计算结果的顺序是先计算子结点的结果，后计算当前结点的结果，该顺序实质是后序遍历。由于在计算每个结点的结果时，该结点的子结点的结果已知，该结点的结果由子结点的结果决定，因此可以确保结果正确。

代码

class Solution {
    class NodeDepth {
        private TreeNode node;
        private int depth;

        public NodeDepth(TreeNode node, int depth) {
            this.node = node;
            this.depth = depth;
        }

        public TreeNode getNode() {
            return node;
        }

        public int getDepth() {
            return depth;
        }
    }

    public TreeNode subtreeWithAllDeepest(TreeNode root) {
        NodeDepth rootDepth = dfs(root);
        return rootDepth.getNode();
    }

    public NodeDepth dfs(TreeNode node) {
        if (node == null) {
            return new NodeDepth(node, 0);
        }
        NodeDepth left = dfs(node.left), right = dfs(node.right);
        TreeNode leftNode = left.getNode(), rightNode = right.getNode();
        int leftDepth = left.getDepth(), rightDepth = right.getDepth();
        if (leftDepth == rightDepth) {
            return new NodeDepth(node, leftDepth + 1);
        }
        return leftDepth > rightDepth ? new NodeDepth(leftNode, leftDepth + 1) : new NodeDepth(rightNode, rightDepth + 1);
    }
}

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是二叉树的结点数。每个结点都被访问一次。

• 空间复杂度：$O(n)$，其中 $n$ 是二叉树的结点数。空间复杂度主要是深度优先搜索的过程中创建实例的空间和递归调用的栈空间，因此空间复杂度是 $O(n)$。