题目
如下图所示的一棵二叉树的深度、宽度及结点间距离分别为:
- 深度:44
- 宽度:44
- 结点 8 和 6 之间的距离:88
- 结点 7 和 6 之间的距离:33
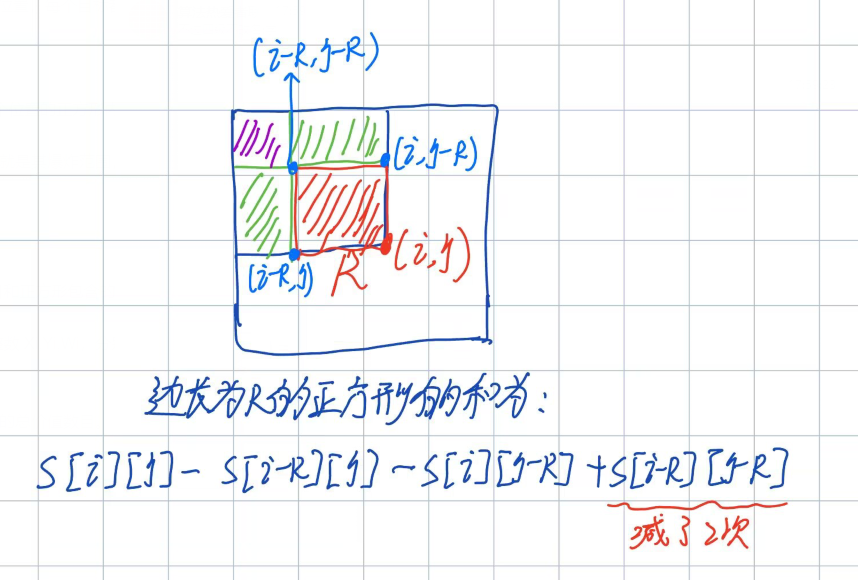
其中宽度表示二叉树上同一层最多的结点个数,节点 u, vu,v 之间的距离表示从 uu 到 vv 的最短有向路径上向根节点的边数的两倍加上向叶节点的边数。
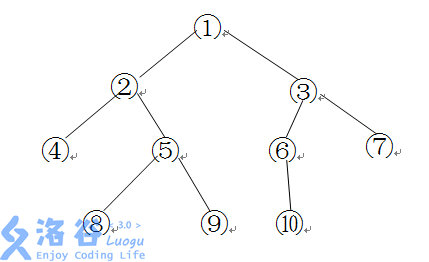
给定一颗以 1 号结点为根的二叉树,请求出其深度、宽度和两个指定节点 x, yx,y 之间的距离。
解答
这一道题分为三个问题,第一个问题是求深度,第二个问题是求最大宽度,第三个问题是求a->b的带权路径长度,这里的权指的是如果是向着跟走的路径权值是2,远离根的路径权值是1,例如8->6,那么8->1的路径是要*2,1->6是不需要的,所以是3*2+2=8,样例也就是这样来的。
对于第一个问题求深度,这个只要走一遍dfs就可以求出答案。
对于第二个问题求宽度,只需要算出每一个点的深度,然后统计每个深度的个数,找最大就可以得出,因为深度不会很深,所以造的桶也不会太多。
主要是第三个问题。第三个问题需要算出路径,考虑使用LCA+倍增算法来求解。
LCA也就是最近公共祖先,有了根节点才可以计算路径权值的分界点和长度。计算LCA的方法有多种,暴力的方法就是直接先统一到同一深度,然后两个同时向上找,直到相遇就算找到,这里的数据量比较小大约是可以通过的,但是一旦数据量变大就难以满足,因此不能一个一个跳,那么就以2的幂次的长度来跳,因为任何整数可以表示成2的幂次的和,因此先大步跳然后减小步幅是可以到达任何深度的。
首先先进行预处理,引入f [i] [j] 表示编号为i的点向上跳2^j到达的点,那么f[i][j]=f[ f[i][j-1] ][j-1],这一步可以这样理解:编号为i的点向上跳2^j等同于先跳2^(j-1)到达f[i][j-1]然后再由f[i][j-1]跳2^(j-1),利用这样的一个递推式,跑一遍dfs就可以预处理出所有点向上跳2的幂次到达的点。
void dfs(int to, int from)//to为当前节点,from为父节点
{
dep[to] = dep[from] + 1;//每个点的深度,也可以进行预处理
f[to][0] = from;
for (int i = 1; i <= lg[dep[to]]; i++)
f[to][i] = f[f[to][i - 1]][i - 1];
for (int i = last[to]; i; i = e[i].next)
if (e[i].to != from)
dfs(e[i].to, to);
}然后接下来进行LCA相关的计算。一般如果没有方向的话,传入参数有两个x,y,分别代表了要计算的起点和终点。大致步骤有两步,第一步是先把两个深度统一,第二步两个点同时向上跳,枚举2的幂次从最大到最后0次,也就是从跳很多步到最后跳一步,因为两个点是一定有公共祖先的,如果跳的很大那么可能一下子找到了非常靠上的祖先,它虽然是公共祖先但却不是最近公共祖先,因此我们要保证跳了之后两个点不会位于同一点(因为位于同一点就代表位于某一层公共祖先了,但是我们无法确定这是否是最近公共祖先),不断缩小步幅,一直到最后两者一定是位于最近公共祖先的左右节点,因为只有这样才能满足最后跳一步都不满足两者位于同一点,而最近公共节点就是两个点的父节点。
当然这道题因为有权值,所以求解过程略有改变,首先是统一深度,因为是x->y,所以x到跟是向根,路径权值为2,根到y是原远离,所以分情况讨论,如果是x深度大,那么在提升的过程中,结果要加上路程*2。然后最后找出共公共祖先,计算公祖祖先深度和统一深度的差值,那么路径长度就知道了,因为长两边是一样的,无非就是一边权值是2,那么结果加上一边路径长度乘3就好了。
int cal(int x, int y)
{
int ans = 0;
if (dep[x] < dep[y])//y先向上走
{
int tmp = dep[y];
while(dep[x]<dep[y])
{
y = f[y][lg[dep[y] - dep[x]] - 1];
}
ans += tmp - dep[y];
}
else//x向上走,这是朝着根的方向
{
int tmp = dep[x];
while (dep[x] > dep[y])
{
x = f[x][lg[dep[x] - dep[y]] - 1];
}
//printf("tmp=%d,dep[x]=%d\n", tmp,dep[x]);
ans += 2 * (tmp - dep[x]);
}
//printf("ans=%d\n", ans);
//接下来找到公共祖先
if (x == y)return ans;//已经找到了
int tmp = dep[x];//存储当前的深度,后面方便计算路径长度
for (int i = lg[dep[x]] - 1;i>=0; i--)
{
if (f[x][i] != f[y][i])
{
x = f[x][i];
y = f[y][i];
}
}
//printf("x=%d\n", x);
//最后的父节点是直接父节点
ans += (tmp - dep[f[x][0]]) * 3;
return ans;
}完整代码
#include<stdio.h>
#include<algorithm>
using namespace std;
#define Max 1000
struct Edge
{
int to, next;
}e[Max];
int last[Max], cnt;
int lg[Max], dep[Max],f[Max][20], deps[20],maxDep;
void add(int from, int to)
{
e[++cnt].to = to;
e[cnt].next = last[from];
last[from] = cnt;
}
void dfs(int to, int from)
{
dep[to] = dep[from] + 1;
deps[dep[to]]++;//统计每一层的个数
maxDep = max(maxDep, dep[to]);
f[to][0] = from;
for (int i = 1; i <= lg[dep[to]]; i++)
f[to][i] = f[f[to][i - 1]][i - 1];
for (int i = last[to]; i; i = e[i].next)
{
//printf("%d %d\n", e[i].next,e[i].to);
if (e[i].to != from)
{
dfs(e[i].to, to);
}
}
}
int cal(int x, int y)
{
int ans = 0;
if (dep[x] < dep[y])//y先向上走
{
int tmp = dep[y];
while(dep[x]<dep[y])
{
y = f[y][lg[dep[y] - dep[x]] - 1];
}
ans += tmp - dep[y];
}
else//x向上走,这是朝着根的方向
{
int tmp = dep[x];
while (dep[x] > dep[y])
{
x = f[x][lg[dep[x] - dep[y]] - 1];
}
//printf("tmp=%d,dep[x]=%d\n", tmp,dep[x]);
ans += 2 * (tmp - dep[x]);
}
//printf("ans=%d\n", ans);
//接下来找到公共祖先
if (x == y)return ans;//已经找到了
int tmp = dep[x];//存储当前的深度,后面方便计算路径长度
for (int i = lg[dep[x]] - 1;i>=0; i--)
{
if (f[x][i] != f[y][i])
{
x = f[x][i];
y = f[y][i];
}
}
//printf("x=%d\n", x);
//最后的父节点是直接父节点
ans += (tmp - dep[f[x][0]]) * 3;
return ans;
}
int n;
int main()
{
scanf("%d", &n);
int x, y;
for (int i = 1; i <= n - 1; i++)
{
scanf("%d%d", &x, &y);
//printf("%d -- %d\n", x, y);
add(x, y);
//printf("%d\n", e[2].to);
//add(y, x);
}
for (int i = 1; i <= n; i++)
lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
dfs(1, 0);//预处理树上倍增
int width = 0;
for (int i = 1; i <= maxDep; i++)
{
width = max(width, deps[i]);
}
scanf("%d%d", &x, &y);
//计算路径
int len = cal(x, y);//计算x->y的宽度
printf("%d\n%d\n%d\n", maxDep, width, len);
return 0;
}