地图上有 N 个目标，用整数 Xi,Yi 表示目标在地图上的位置，每个目标都有一个价值 Wi。

注意：不同目标可能在同一位置。

现在有一种新型的激光炸弹，可以摧毁一个包含 R×R 个位置的正方形内的所有目标。

激光炸弹的投放是通过卫星定位的，但其有一个缺点，就是其爆炸范围，即那个正方形的边必须和 x，y 轴平行。

求一颗炸弹最多能炸掉地图上总价值为多少的目标。

输入格式
第一行输入正整数 N 和 R，分别代表地图上的目标数目和正方形包含的横纵位置数量，数据用空格隔开。

接下来 N 行，每行输入一组数据，每组数据包括三个整数 Xi,Yi,Wi，分别代表目标的 x 坐标，y 坐标和价值，数据用空格隔开。

输出格式
输出一个正整数，代表一颗炸弹最多能炸掉地图上目标的总价值数目。

数据范围
0≤R≤10^9
0<N≤10000,
0≤Xi,Yi≤5000
0≤Wi≤1000
输入样例：
2 1
0 0 1
1 1 1
输出样例：
1

分析

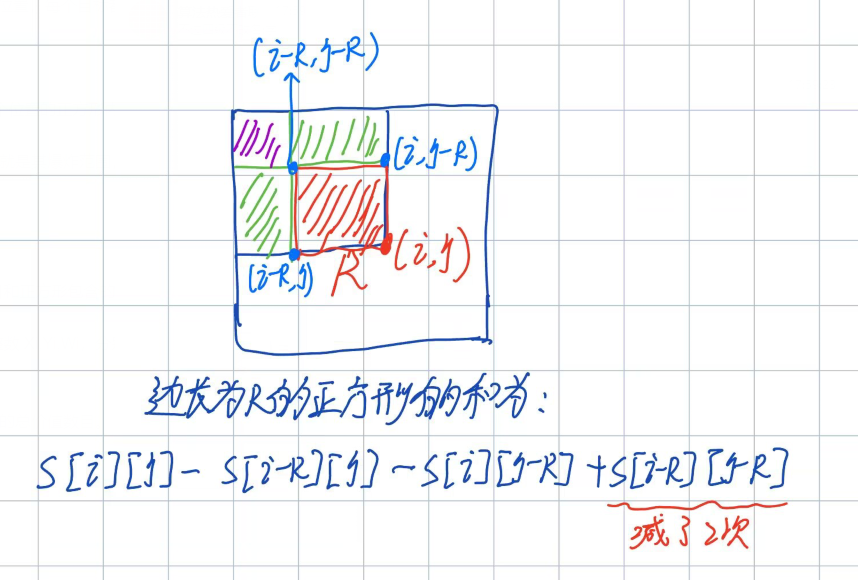
1. 首先看一下X的范围，就知道了矩阵的大小，那么O(n^2)的复杂度即可解决，然后比较明显是一个二维前缀合问题。可以参考：1224：最大子矩阵——子矩阵、二维前缀和，和那个挺像，但是 上个题需要两个点（左上、右下）才能确定一个矩阵，所以需要四层for；这个题比较特殊，由于是一个正方形，所以已知一个右下角的点，就可以确定一个矩阵（左上角(i-R,j-R)），两层for即可解决，O(n^2)；
2. 题意：给出正方形的大小，看看它在什么位置，价值最大，与正方形同边的区域不算，那么就相当于求（R-1）*（R-1）的正方形面积所能达到的最大价值；
3. 那就直接枚举这个正方形的右下角坐标，取所包围的正方形面积的最大价值；这里直接从(R,R)枚举到(5001,5001)，当然也可以用个变量记录下x、y的最大值，枚举到x，y的最大值；
4. 由于前缀和坐标从1开始，所以输入时整体坐标+1；且不同目标可能在同一位置，所以s[++x][++y] += w，注意是 +=；
5. 由于X、Y的最大值就是5000，所以整个坐标系最大就是5000*5000，所以R的值可以预处理一下，因为太大的R没必要；还有就是这题开两个数组MLE，所以直接用输入时的数组，滚动数组即可；

#include <bits/stdc++.h>

using namespace std;

const int N = 5010;

//即表示初始数组，也表示前缀和
int s[N][N];
int n, R, ans;

int main() {
    cin >> n >> R;
    //X,Y<=5000，所以R取5001就能包含整个矩阵了
    R = min(R, 5001);
    for (int i = 0; i < n; ++i) {
        int x, y, w;
        cin >> x >> y >> w;
        //1.二维前缀和坐标从1开始的，所以整体+1
        //2.一个点（x,y）可能有多个目标
        s[++x][++y] += w;
    }
    //初始前缀和数组
    for (int i = 1; i <= 5001; ++i) {
        for (int j = 1; j <= 5001; ++j) {
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
        }
    }
    //枚举矩阵的右下角坐标(i,j)，左上角就是(i-r,j-r)
    for (int i = R; i <= 5001; ++i) {
        for (int j = R; j <= 5001; ++j) {
            int t = s[i][j] - s[i - R][j] - s[i][j - R] + s[i - R][j - R];
            ans = max(ans, t);
        }
    }
    cout << ans;
    return 0;
}