人工智能：一种现代的方法 第十四章 概率推理

本章前言

上一部分我们讲了确定性问题，确定性问题域是在知识表示中，使用精确的形式表达知识，如逻辑规则、数学公式等。在推理过程中，基于逻辑推理或数学推理规则进行推断，例如演绎推理或归纳推理。这种问题域的特点是结果是确定的，不涉及概率或不确定性，因此可以使用形式化的推理方法来解决问题。而对于不确定问题，是没办法的。而本章讲述的就是不确定性问题

14.1 不确定性问题域中的知识表示

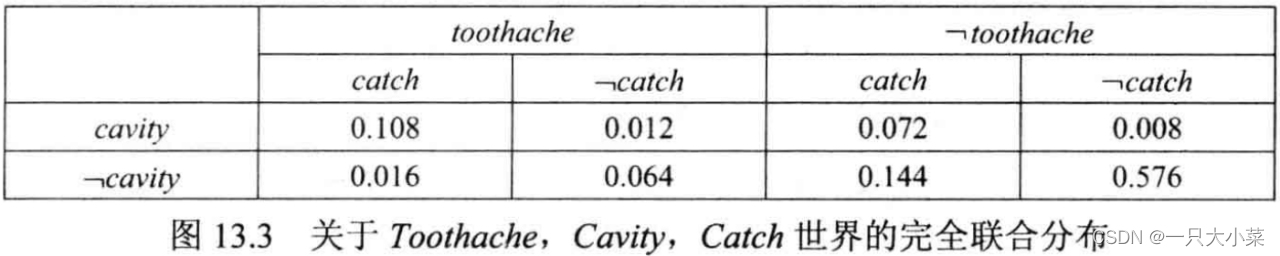
14.1.1 联合概率分布

14.1.2贝叶斯网络

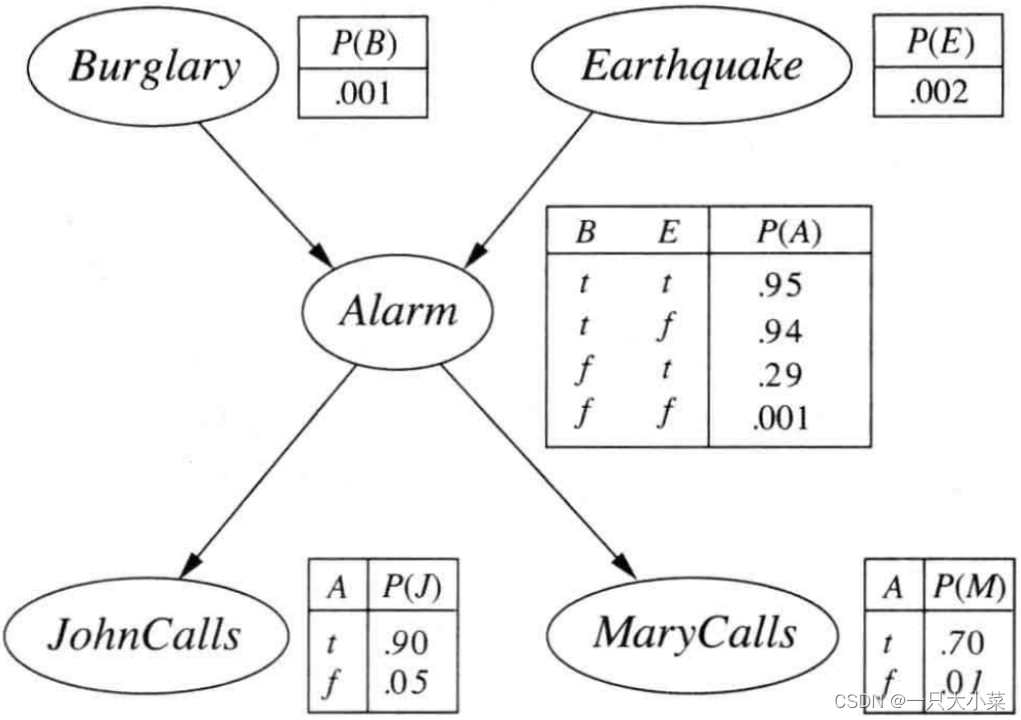
贝叶斯网络是一个有向无环图每个节点对应一个随机变量，可以是离散变量也可以是连续变量一组有向边连接节点对每个节点Xi有一个条件分布P(Xi|Parents(Xi))

	贝叶斯网络表示	联合概率分布表示
类型	图形模型	概率表示
表示方式	有向无环图	条件概率表（CPT）
结构	节点表示变量，边表示依赖关系	无显式图结构
推理和推断	使用图结构和条件概率表进行推理和推断	使用乘积规则和边缘化规则进行计算和推断
用途	表示变量之间的依赖关系和概率关系	表示多个变量之间的概率关系

14.2 贝叶斯网络的语义

14.2.1表示联合概率分布

P(x₁, …, xₙ) = Π P(xᵢ | parents(Xᵢ))

整个贝叶斯网络的联合概率分布可以通过将每个变量的条件概率分布 P(xᵢ | parents(Xᵢ)) 进行乘积来得到。每个条件概率分布表示了变量 xᵢ 在给定其父节点的取值情况下的概率分布。通过乘积规则，我们可以计算出整个网络中所有变量同时取不同取值的联合概率分布。

14.2.2 紧致性

• 局部结构化（locally structured, 也称稀疏，sparse）：每个子部件只与有限数量的的其他部件之间有直接相互作用

• 例如：贝叶斯网络中每个节点有5个父节点，当所有变量为布尔变量，总节点数n=30时，贝叶斯网络只需要960个参数，完全联合分布需要超过10亿个参数

• 技巧：过于微弱的依赖关系，不增加边，尽管会损失一点精度

14.2.3 节点排序

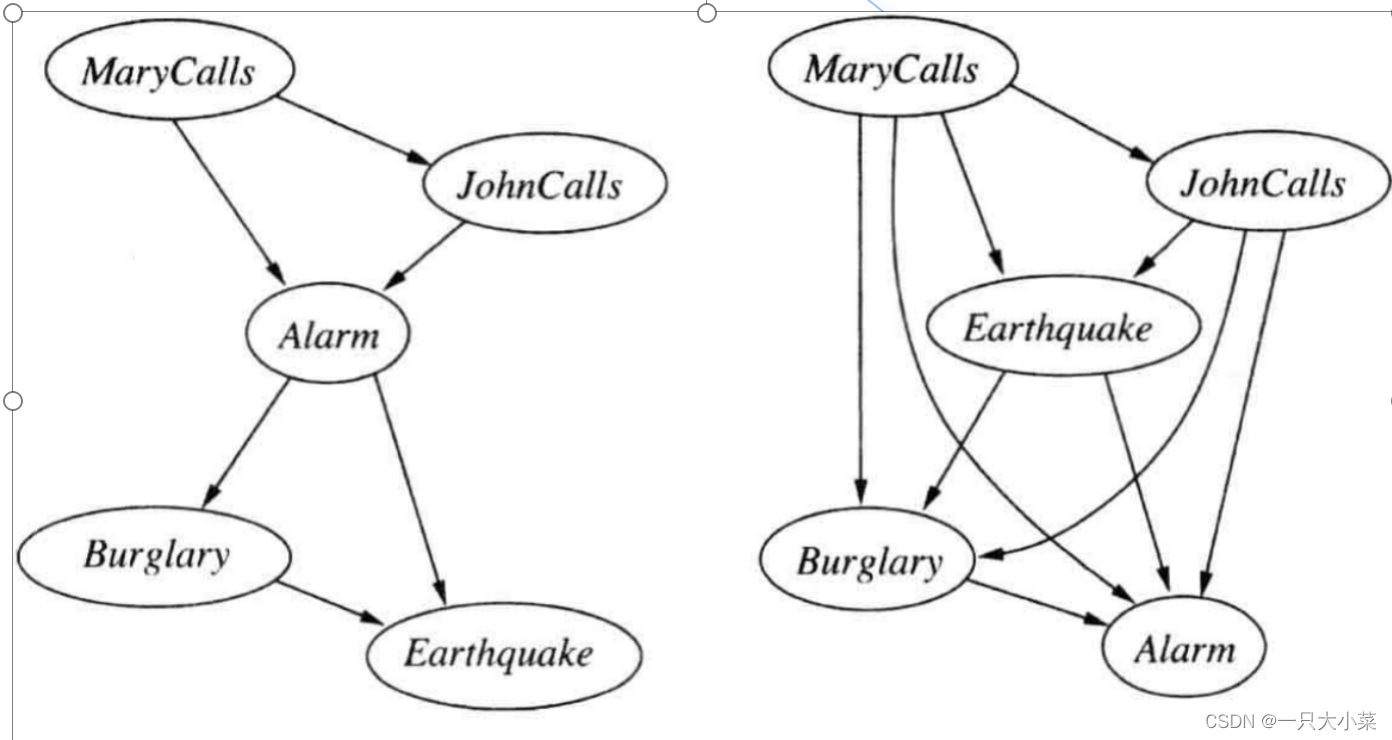
节点排序的选择可以影响贝叶斯网络的推理效率和计算复杂度，因此需要根据具体情况选择合适的排序方法。

14.2.4 贝叶斯网络中的条件独立关系

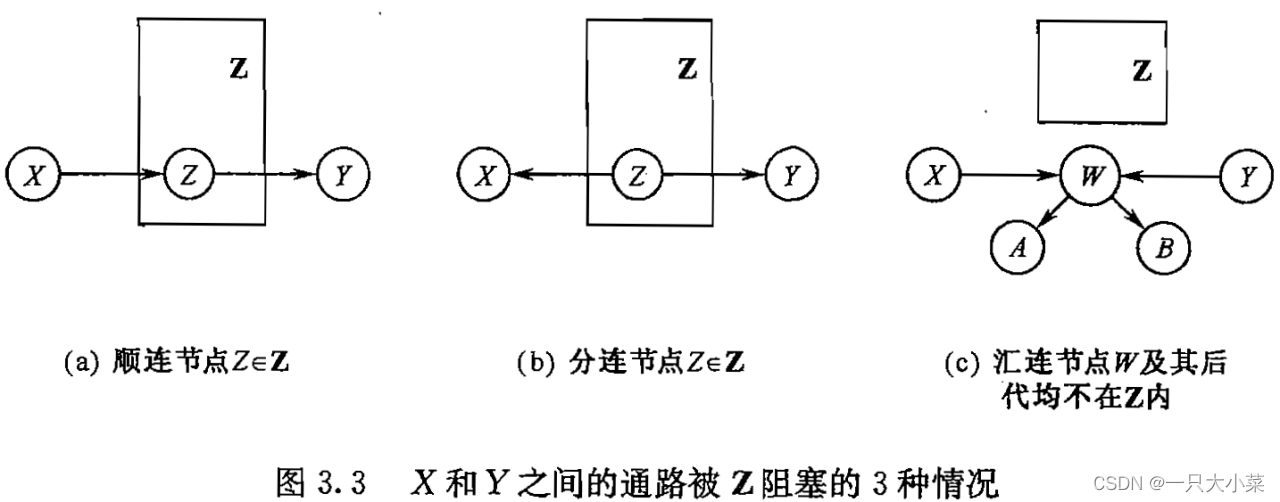
三种常见的连接方式

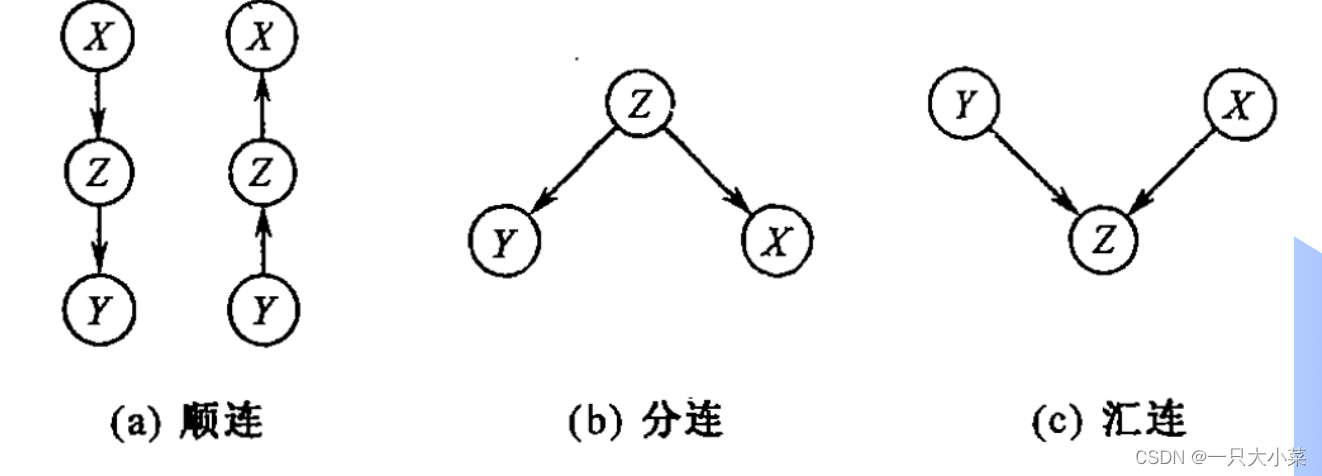
• 顺连（Serial Connection）：顺连是指一个节点依赖于另一个节点，并且它们之间没有其他节点介入。在贝叶斯网络中，顺连表示一个变量直接依赖于另一个变量，没有其他中间节点的干预。顺连通常用于表示因果关系或直接影响关系
• 汇连（Cascade Connection）：汇连是指一个节点同时依赖于多个节点，而这些节点之间没有依赖关系。在贝叶斯网络中，汇连表示一个变量依赖于多个其他变量，且这些变量之间没有直接的依赖关系。汇连通常用于表示多个因素对一个结果的影响。
• 分连（Common Cause Connection）：分连是指多个节点同时依赖于一个公共的节点。在贝叶斯网络中，分连表示多个变量共同依赖于一个变量，该变量通常被称为共同父节点。分连通常用于表示多个变量之间的共同因素或共同影响。

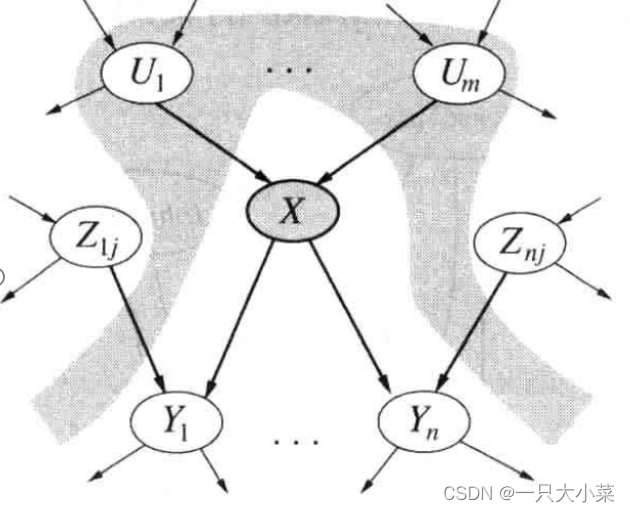
贝叶斯网络中的条件独立关系 一
给定父节点，结点条件独立于其他祖先结点

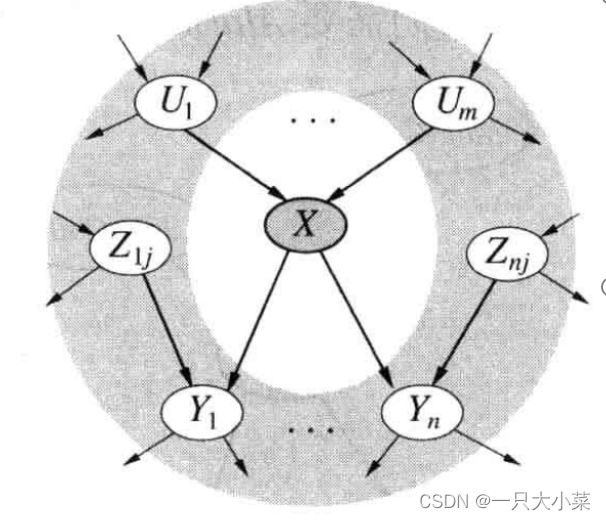
贝叶斯网络中的条件独立关系 二
给定节点的马尔科夫覆盖，即父节点、子节点及子节点的父节点，节点条件独立于其他节点

贝叶斯网络中的条件独立关系 三

14.3 条件分布的有效表示

条件分布的有效表示方法取决于具体的问题和概率模型。以下是几种常见的条件分布表示方法

条件概率表

CPT 是一种常见的表示条件分布的方法，特别适用于离散型变量。CPT 是一个表格，其中每一行表示给定父节点取值情况下，该节点的条件概率分布。

确定性节点
父节点：Canadian、US、Mexican 子节点：NorthAmerican 析取关系
父节点：销售同产品商家子节点：喜欢还价的买家 最小关系

噪声或节点
父节点：Cold（感冒）、Flu（流感）、Malaria（疟疾）子节点：Fever（发烧） Noisy-OR关系

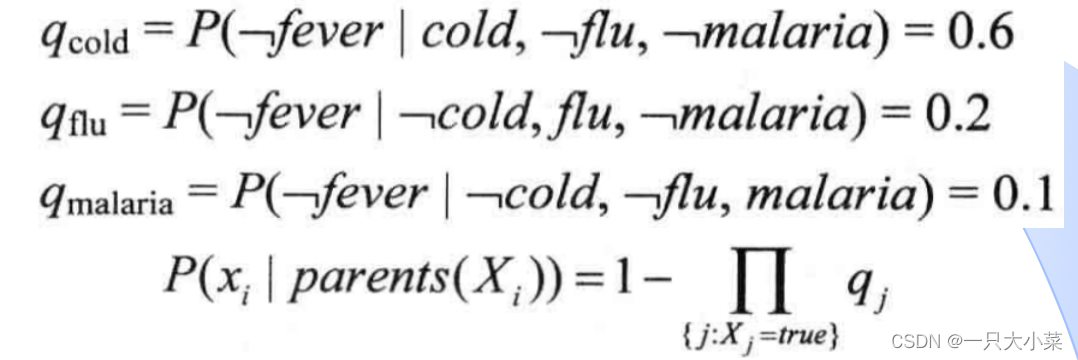
包含连续变量的贝叶斯网络

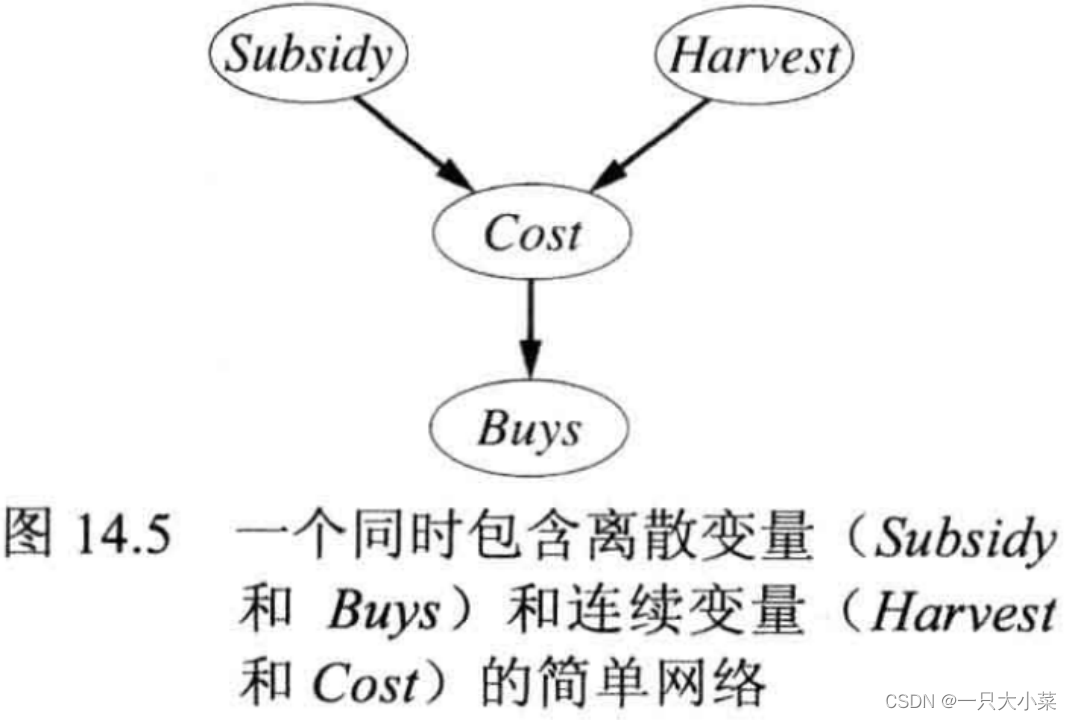
• 离散化，损失精度
• 混合贝叶斯网络：同时包含连续和离散变量

离散父节点的连续分布：线性高斯分布

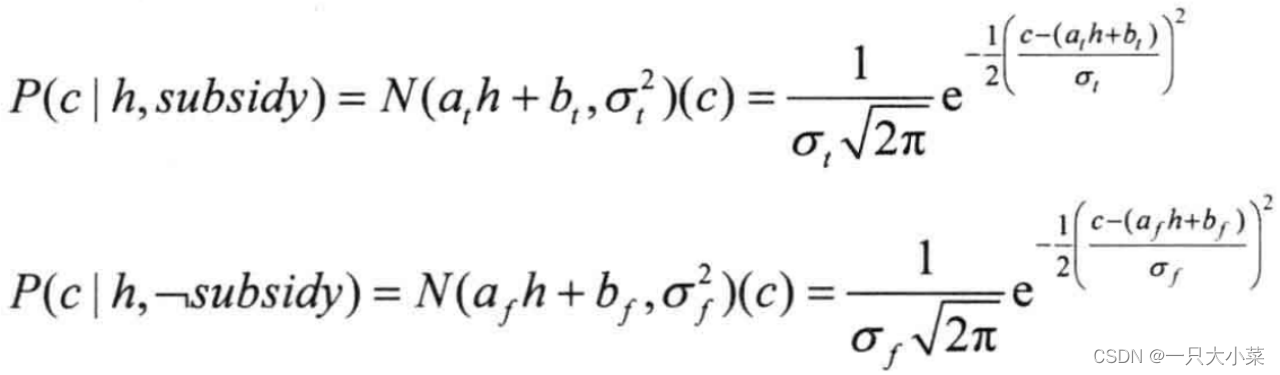
14.4 贝叶斯网络的精确推理

贝叶斯网络中存在三种变量 ：证据变量、查询变量、隐藏变量

14.4.1通过枚举进行推理

def ENUMERATION_ASK(X, e, bn):
  
    Q = {}  # 初始化查询变量X的分布
    for xi in X:
        Q[xi] = ENUMERATE_ALL(bn.VARS, extend(e, X=xi))  # 对每个X的取值，使用ENUMERATE_ALL计算分布
    return NORMALIZE(Q)  # 对分布进行归一化

def ENUMERATE_ALL(vars, e):
  
    if not vars:  # 如果变量集合为空，返回概率1.0
        return 1.0
    Y = vars[0]  # 获取第一个变量Y
    if Y in e:  # 如果Y在观测到的变量值e中
        return P(Y, e[Y], parents(Y)) * ENUMERATE_ALL(vars[1:], e)  # 返回P(Y|parents(Y)) * 递归计算剩余变量的概率
    else:
        total = 0.0
        for y in domain(Y):  # 遍历Y的所有取值
            ey = extend(e, Y=y)  # 将观测到的变量值e扩展为包含Y=y的新观测值
            total += P(Y, y, parents(Y)) * ENUMERATE_ALL(vars[1:], ey)  # 累加P(Y=y|parents(Y)) * 递归计算剩余变量的概率
        return total

14.4.2变量消元算法

逐点相乘

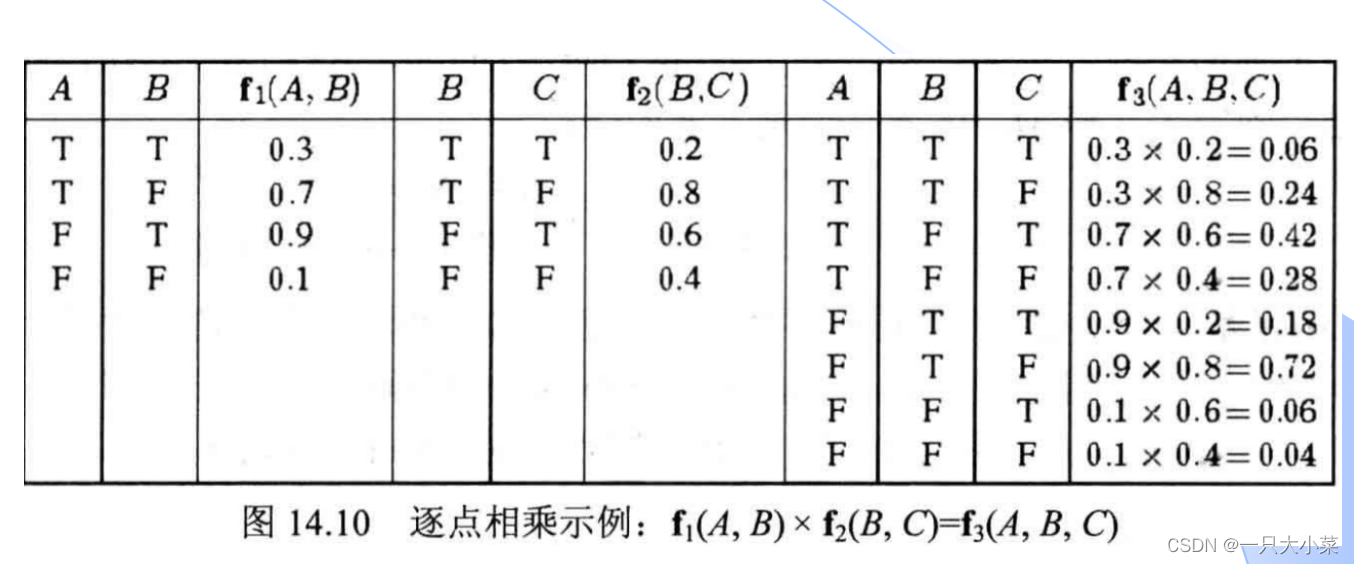
消元过程

def ELIMINATION_ASK(X, e, bn):
   
    factors = []
    for var in ORDER(bn.VARS):  # 按顺序处理变量
        factors.append(MAKE_FACTOR(var, e))  # 创建因子
        if var in X:  # 如果变量是查询变量
            factors = SUM_OUT(var, factors)  # 求和消除变量
    return NORMALIZE(POINTWISE_PRODUCT(factors))  # 归一化因子的点积

14.4.5精确推理的复杂度

精确推理的复杂度与贝叶斯网络的结构相关
单连通（多形树，polytree）：线性
多连通：比NP完全还难

14.5 贝叶斯网络中的近似推理

14.5.1直接采样算法

直接采样适用于没有证据变量的情况下，只需要对贝叶斯网络中一部分随机变量的边缘分布进行采样，可以用直接采样对全部随机变量进行采样。

def PRIOR_SAMPLE(bn):
    x = {}
    for node in bn.nodes():
        x[node] = sample_from_distribution(bn, node, x)
    return x

def sample_from_distribution(bn, node, x):
    parents = bn.parents(node)
    parent_values = [x[parent] for parent in parents]
    probabilities = bn.get_probability(node, parent_values)
    return random.choices(bn.get_domain(node), probabilities)[0]

14.5.2 拒绝采样算法

import random

def REJECTION_SAMPLING(X, e, bn, N):
    counts = {value: 0 for value in bn.get_domain(X)}  # 初始化计数器
    
    for _ in range(N):
        x = {}  # 存储样本的字典
        for node in bn.nodes():
            x[node] = sample_from_distribution(bn, node, x)  # 从概率分布中采样得到样本
        
        if is_consistent(x, e):  # 判断样本是否与观测值一致
            counts[x[X]] += 1  # 更新相应取值的计数器
    
    total = sum(counts.values())  # 计算计数器的总和
    return {value: count / total for value, count in counts.items()}  # 归一化计数器得到概率分布


def sample_from_distribution(bn, node, x):
    parents = bn.parents(node)  # 获取节点的父节点
    parent_values = [x[parent] for parent in parents]  # 获取父节点的取值
    probabilities = bn.get_probability(node, parent_values)  # 获取节点的条件概率分布
    return random.choices(bn.get_domain(node), probabilities)[0]  # 根据概率分布进行采样

直接采样适用于没有证据变量的情况下，当存在证据变量时直接采样法就失效了。如何解决呢最直接的方法是拒绝采样，还是利用直接采样得到所有变量的取值。如果这个样本在观测变量上的采样值与实际观测值相同，则接受，否则拒绝，重新采样。这种方法的缺点是采样效率可能会非常低，随着观测变量个数的增加、每个变量状态数目的上升，拒绝采样法的采样效率急剧下降，实际中基本不可用。

15.5.3 似然加权

import random

def likelihood_weighting(X, e, bn, N):
    # X: 查询变量
    # e: 观察到的变量值
    # bn: 贝叶斯网络
    # N: 生成的样本总数

    # 初始化权重计数向量
    W = [0] * len(X)

    for j in range(N):
        x, w = weighted_sample(bn, e)
        # 根据查询变量的值累积权重
        W[X.index(x)] += w

    return normalize(W)

def weighted_sample(bn, e):
    # bn: 贝叶斯网络
    # e: 观察到的变量值

    w = 1
    x = {}

    for Xi in bn.variables:
        if Xi in e:
            # 如果变量是观察到的变量，则根据观察到的值更新权重
            w *= bn.probability(Xi, e[Xi])
        else:
            # 对于非观察到的变量，根据给定其已采样的父节点值的条件分布进行采样
            x[Xi] = sample_from_conditional(Xi, e, bn)
    
    return x, w

def sample_from_conditional(Xi, e, bn):
    parents = bn.parents(Xi)
    parent_values = [e[parent] for parent in parents]
    conditional = bn.conditional_distribution(Xi, parent_values)
    # 从条件分布中随机采样一个值
    return random.choices(conditional.values, weights=conditional.probabilities)[0]

在实际应用中，可以参考重要性采样的思想，不再对观测变量进行采样，只对非观测变量采样，但是最终得到的样本需要赋一个重要性权值

14.5.4 基于马尔可夫链的推理

def GIBBS_ASK(X, e, bn, N):
    counts = {value: 0 for value in bn.get_domain(X)}
    x = e.copy()  # 初始化x为观测值e的副本
    
    Z = bn.get_non_evidence_variables()  # 获取非证据变量Z
    
    for _ in range(N):
        for Z_var in Z:
            x[Z_var] = sample_from_distribution(bn, Z_var, x)  # 从条件概率分布中采样Z_var的值
        
        counts[x[X]] += 1  # 更新相应取值的计数器
    
    return NORMALIZE(counts)

吉布斯抽样（Gibbs sampling）是一种马尔可夫链蒙特卡罗（MCMC）方法，用于从多变量概率分布中抽取样本。上述步骤描述了基本的吉布斯抽样算法：

• 初始化：随机选择第一个样本 Θ₁ = (θ₁₁, θ₂₁)。
• 根据当前的 θ₂ᵢ，从条件概率分布 p(θ₁|θ₂=θ₂ᵢ, x₁,…,xₙ) 中抽取 θ₁ᵢ₊₁。
• 根据当前的 θ₁ᵢ₊₁，从条件概率分布 p(θ₂|θ₁=θ₁ᵢ₊₁, x₁,…,xₙ) 中抽取 θ₂ᵢ₊₁。得到新的样本 Θᵢ₊₁。

重复步骤 2 和 3，直到满足抽样需求，得到样本序列 {Θ₁, …, Θₙ}。
在吉布斯抽样过程中，每个样本 Θᵢ 受到前一个样本 Θᵢ₋₁ 的影响。这意味着通过吉布斯抽样得到的样本序列 {Θ₁, …, Θₙ} 是一条马尔可夫链。这种方法通常用于无法直接从联合分布中抽取样本的情况下，通过条件分布进行抽样。