文章目录
- Leecode 704.二分查找
- 题目连接:[Leecode 704.二分查找](https://leetcode.cn/problems/remove-element/)
- 遇到的问题
- 题目
- 二分法的第一种写法 (左闭右闭)
- 第二种解法(左闭右开 代码呈现)
- Leecode 27.移除元素
- 题目链接:[Leecode 移除元素](https://leetcode.cn/problems/remove-element/)
- 遇到的问题
- 代码实现
- 暴力解法
- 快慢指针
- 总结
- 今日收获
Leecode 704.二分查找
题目连接:Leecode 704.二分查找
遇到的问题
对右位运算符那块不太理解后来 方大佬給整明白了。
题目
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。

示例1
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例2
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
思路
这道题目的前提是数组为有序数组,同时题目还强调数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的,这些都是使用二分法的前提条件,当大家看到题目描述满足如上条件的时候,可要想一想是不是可以用二分法了。
在决定使用二分查找法之前,确定数组是否有序,如果没有 要进行排序操作
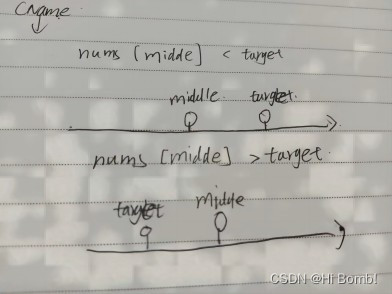
二分查找涉及的很多的边界条件,逻辑比较简单,但就是写不好。例如到底是 while(left < right) 还是 while(left <= right),到底是right = middle呢,还是要right = middle - 1呢?
边界条件是一大难点,即确定是左闭右闭还是左闭右开
如果是右闭的情况 即下标等于right 那么在移动下标时就要注意 要减去重合得地方 所以
下一个right = middle -1
大家写二分法经常写乱,主要是因为对区间的定义没有想清楚,区间的定义就是不变量。要在二分查找的过程中,保持不变量,就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作,这就是循环不变量规则。
写二分法,区间的定义一般为两种,左闭右闭即[left, right],或者左闭右开即[left, right)。
下面我用这两种区间的定义分别讲解两种不同的二分写法。
接下来就来演示代码
二分法的第一种写法 (左闭右闭)
第一种写法,我们定义 target 是在一个在左闭右闭的区间里,也就是[left, right] (这个很重要非常重要)。
区间的定义这就决定了二分法的代码应该如何写,因为定义target在[left, right]区间,所以有如下两点:
- while (left <= right) 要使用 <= ,因为left == right是有意义的,所以使用 <=
- if (nums[middle] > target) right 要赋值为 middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
例如在数组:1,2,3,4,7,9,10中查找元素2,如图所示:

下面提供我的AC代码
> public class BinarySearch {
//先做左闭右闭的情况
public int search(int nums[],int target) {
//避免当target 小于nums[0] ,nums[nums.lenth-1] 时多循环运算
if (target < nums[0] || target > nums[nums.length-1])
// 这里呢 进行一个排除 如果说目标的值小于最小 大于最大,那就直接退出
//运算了
{
return -1;
}
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int middle = left + ((right - left) / 2); //这里防止溢出
// 右位运算符的而写法是
//int middle =left+ ((right-left)>>1); //下面详细解释一下为什么这么左
if (nums[middle] > target) {
right = middle - 1; //这部分的理解 可以通过画图来深刻了解一下
} else if (nums[middle] < target) {
left = middle + 1;
} else {
return middle;
}
}
return -1;
}
通过我画的这个图就可以试着理解一下 right 和left下标的运动原理了
右位运算符这里引用一下 大佬的原文
int middle =left+ ((right-left)>>1);
这个写法等同于(left + right ) / 2,
如果right - left的结果是一个奇数,就会算出一个浮点数出来,比如5 / 2的结果是2.5,数组里没有2.5 这个下标的元素,这就看你用的语言默认取整是怎么做的,所以就会出现问题。用右移运算符是直接做位运算,遇到奇数也能解决。
第二种解法(左闭右开 代码呈现)
// 左闭右开
public int search2(int nums[],int target )
{
int left=0;
int right=nums.length;
while(left<right) {
int middle = left + ((right - left)>>1); // 在左闭右开的情况下这个middle 的取值
//什么是右运算符
if(nums[middle]> target)
{
right=middle;
}
else if(nums[middle]<target)
{
left=middle+1; // 这里需要注意 因为左闭所以要注意左边下标在变化的时候要+1;
}
else
{
return middle;
}
}
return -1; //退出
}
}
Leecode 27.移除元素
题目链接:Leecode 移除元素
遇到的问题
暴力解法很自在,一看就懂 两个循环 第一次在数组遍历
第二次 如果if相同就在将数组进行进位变化
快慢指针解法
之前一听指针脑袋都大 ,今天弄完感觉还行
代码实现
暴力解法
public int remove(int nums[],int var)
{
int size =nums.length; //遍历需要的范围,也就是数组的长度
//第一波循环遍历数组寻找 等于 var
for(int i=0;i<size;i++)
{
if(nums[i]==var) //第二次循环就是将数组迁移
{
for(int j=i+1; j<size;j++)
{
nums[j - 1] = nums[j];
}
i--;
size--;
}
}
return size;
}
快慢指针
//快慢指针的remove
public int remove2(int nums[],int var)
{
int size =nums.length;
int slowIndex=0 ;//定义慢指针;只需要一层for循环
for (int fastIndex=0;fastIndex<size;fastIndex++) //fastIndex是数组中不等于var的下标
{
if (nums[fastIndex]!=var) //slowIndex是新数组的下标
{
nums[slowIndex++] = nums[fastIndex]; //则把不等于要删除的值都放到新数组里,最后返回一个
}
}
return slowIndex; //新数组中的大小;
}
}
总结
1.暴力解法
在找到要移除的val后,数组整体左移进行删除,此时在进入下一次循环时需要考虑到指针i的位置发生了变化,数组的长度也发生了变化,因此需要更新二者后再进入循环。
2.双指针法
定义快慢指针,快指针遍历数组,寻找val之外的元素,组成不含val元素的新数组;
慢指针指向新数组的元素,一次循环后需要右移一位以便接收下次循环快指针找到的元素,当快指针遍历完nums,快指针的下标实际上就是新数组的长度。
在原数组的废墟上建立新的堡垒
今日收获
1 第一次AC 然后满兴奋的,
2 一有问题大家解决的好快,自己感觉写的博文还有些乱
3 向方大佬致敬 我也打算弄一下模板了 不然要好久