目录

前言

一、数据预处理定义

二、波士顿房价数据进行数据预处理

2.1 下载波士顿房价数据集

 2.2 查看数据集的描述、特征及数据条数、特征数量

2.3 将数据读入pandas的DataFrame并转存到csv文件

2.4 查看数据集各个特征的类型以及是否有空值

2.5 对数据集做中心化度量：计算各个特征的中位数和均值，分析中位数和均值情况

2.6 对数据集做离散化度量：对第一个特征画盒图（箱线图），检查孤立点（离群点）

2.7 对所有特征画盒图（箱线图），检查孤立点（离群点）

2.8 对第一个特征排序后画散点图

2.9 对第一个特征画分位数图

2.10 对所有特征画分位数图

2.11 使用线性回归方法拟合第一个特征

2.12 使用局部回归（Loess）曲线（用一条曲线拟合散点图）方法拟合第一个特征数据

2.13 对第三个特征分两段画分位数-分位数图

2.14 画直方图，查看各个特征的分布和数据倾斜情况

2.15 对所有特征画直方图，查看数据的分布和数据倾斜情况

2.16 寻找所有特征之间的相关性并找出相关性大于 0.7 的特征对，做特征规约

三、波士顿房价数据进行模拟训练（切分数据集7:3）

3.1 将数据集按7:3的比例切分为训练集和测试集，对全部特征（不切片）使用线性回归算法进行训练，显示训练集拟合度和测试集拟合度

3.2 对数据集进行按列归一化操作，使用梯度下降算法进行训练，显示训练集拟合度和测试集拟合度

3.3 将随机森林算法用于回归问题：将波士顿房价数据集按7:3切分为训练集和测试集，使用随机森林回归器进行训练，显示训练集准确度和测试集准确度

3.4 将GBDT算法用于回归问题：将波士顿房价数据集按7:3切分为训练集和测试集，使用GBDT回归器进行训练，显示训练集准确度和测试集准确度

3.5 将岭回归算法用于回归问题：将波士顿房价数据集按7:3切分为训练集和测试集，使用岭回归算法进行训练，显示训练集拟合度和测试集拟合度；导入sklearn的MSE和MAE方法计算均方误差和平均绝对误差评价指标

3.6 测试值与预测值之间的差距

总结

---

前言

根据数据预处理的过程和步骤，对波士顿房价数据集进行数据预处理和模型训练（需要将数据集切分为训练集和测试集）在进行模型训练时进行数据按列归一化、特征规约/特征抽取等数据预处理操作，训练出高分模型后在测试集上进行测试，在测试集上验证准确度。这几天没有更新就是在做这个数据预处理的大作业和其他的大作业。现在总算是做完了，发上来大家一起研究讨论讨论，有什么不足的地方还请评论出来，我们一起学习~

---

一、数据预处理定义

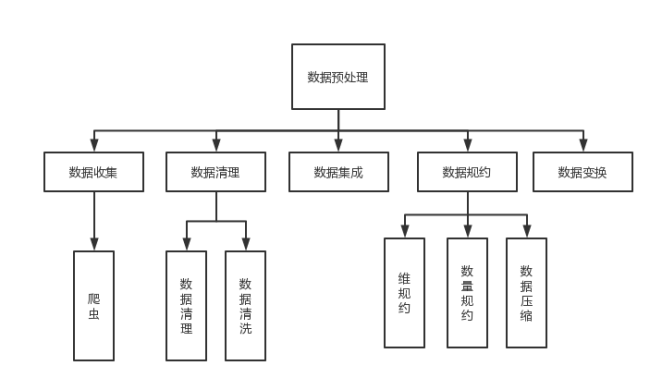
数据预处理（Data Preprocessing）是指在对数据进行挖掘以前，需要对原始数据进行清理、集合和变换等一系列处理工作，以达到挖掘算法进行知识获取研究所要求的最低规范和标准。通过数据预处理工作，可以使残缺的数据完整，并将错误的数据纠正、多余的数据去除，进而将所需的数据进行数据集成。数据预处理的常见方法有数据清洗、数据集成和数据变换。

总体的流程图如下图所示：

 

二、波士顿房价数据进行数据预处理

2.1 下载波士顿房价数据集

代码：

from sklearn.datasets import load_boston

housing = load_boston()
print(housing.keys())

效果图：

 2.2 查看数据集的描述、特征及数据条数、特征数量

代码：

print(housing.DESCR)
print(housing.feature_names)

X=housing.data
print(X.shape,X)
y=housing.target
print(y.shape,y)

 效果图：

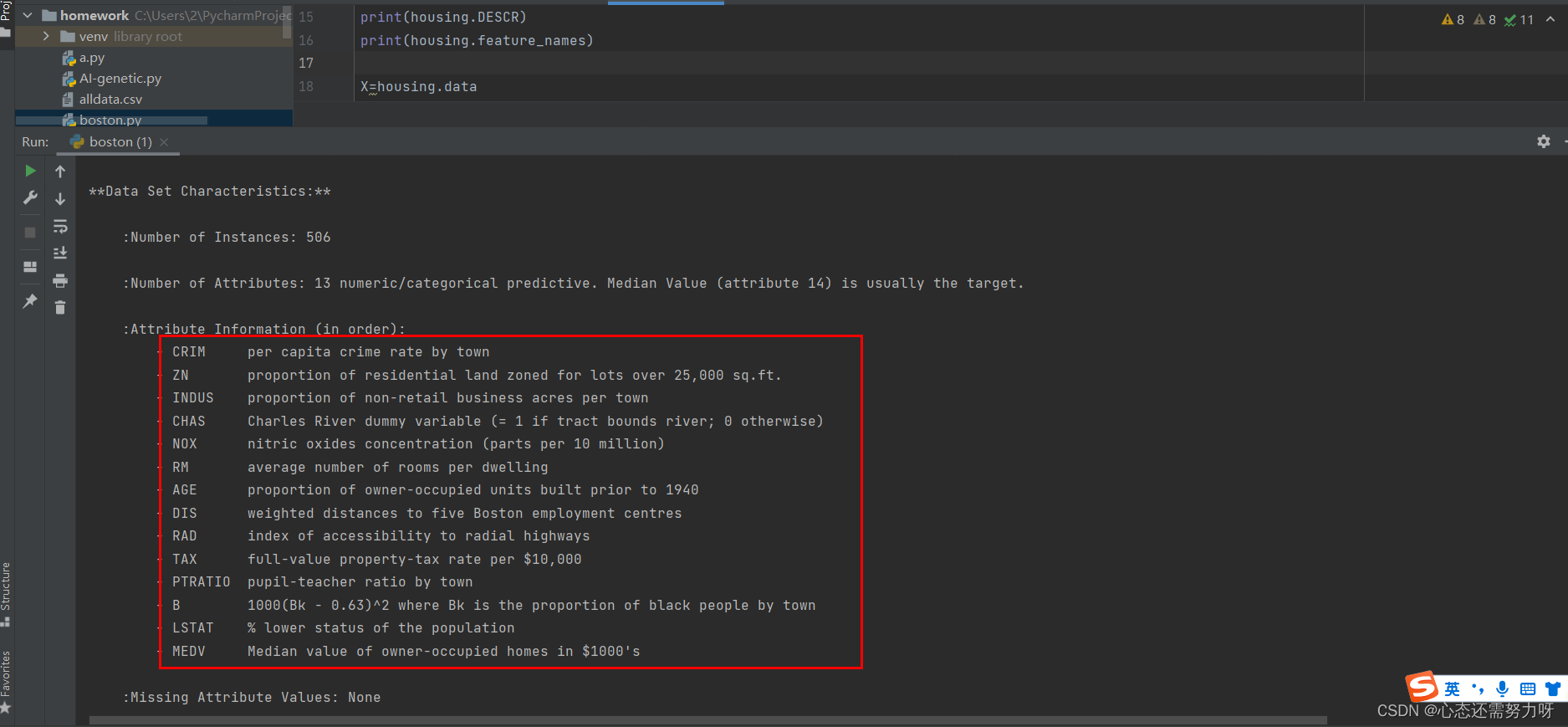
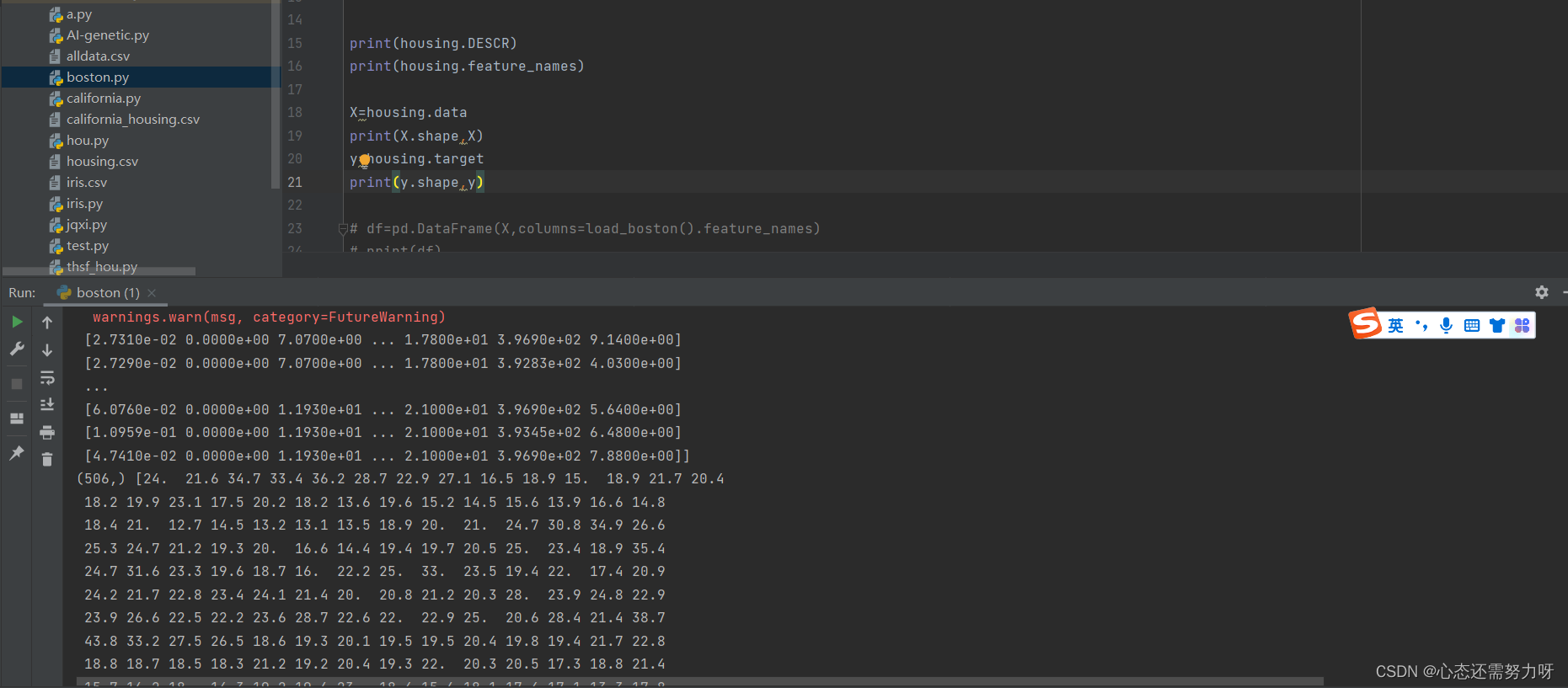
 分析：可看出波士顿房价有506条数据，13个特征。

 每个特征的中文含义如下：

CRIM: 城镇人均犯罪率
ZN: 住宅用地所占比例
INDUS: 城镇中非商业用地所占比例
CHAS: 查尔斯河虚拟变量,用于回归分析
NOX: 环保指数
RM: 每栋住宅的房间数
AGE: 1940 年以前建成的自住单位的比例
DIS: 距离 5 个波士顿的就业中心的加权距离
RAD: 距离高速公路的便利指数
TAX: 每一万美元的不动产税率
PTRATIO: 城镇中的教师学生比例
B: 城镇中的黑人比例
LSTAT: 地区中有多少房东属于低收入人群

2.3 将数据读入pandas的DataFrame并转存到csv文件

代码：

import pandas as pd
df=pd.DataFrame()
for i in range(X.shape[1]):
    df[housing.feature_names[i]]=X[:,i]
df['target']=y
df.to_csv('boston_housing.csv',index=None)
print(df)

效果图：

 分析：已经生成.csv文件，并且数据已经存储进去，打印出的效果图如上图所示。

2.4 查看数据集各个特征的类型以及是否有空值

代码：

print(df.info())

效果图:

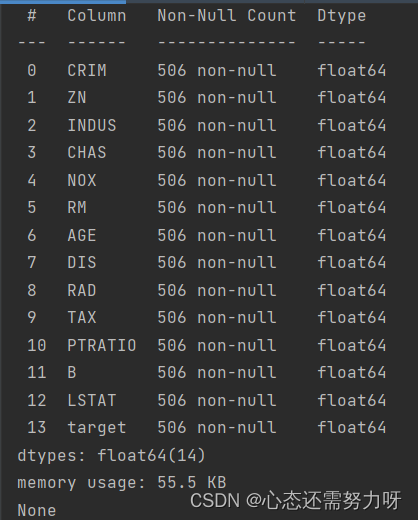
 分析：可从上图中看到没有空值。

2.5 对数据集做中心化度量：计算各个特征的中位数和均值，分析中位数和均值情况

代码：

print(df.describe())

效果图：

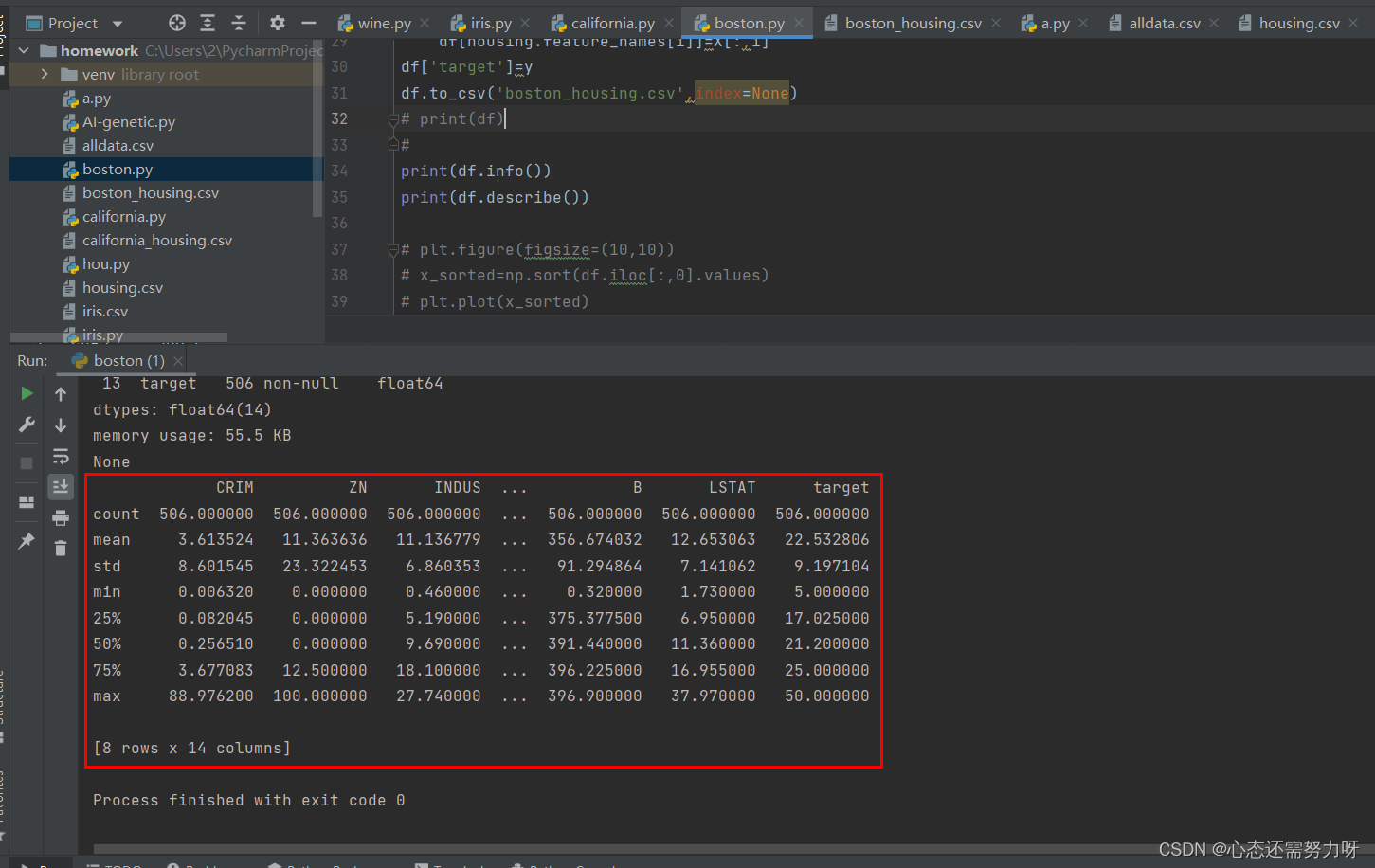
 分析：可从上图中看到波士顿房价的每一个特征的均值和中位数，个特征的均值和中位数的值还差不多，只有个别特征，如CRIM、ZN这些特征偏离性严重。

2.6 对数据集做离散化度量：对第一个特征画盒图（箱线图），检查孤立点（离群点）

代码：

plt.boxplot(X[:,0],showmeans=True,meanline=True)
plt.show()

效果图：

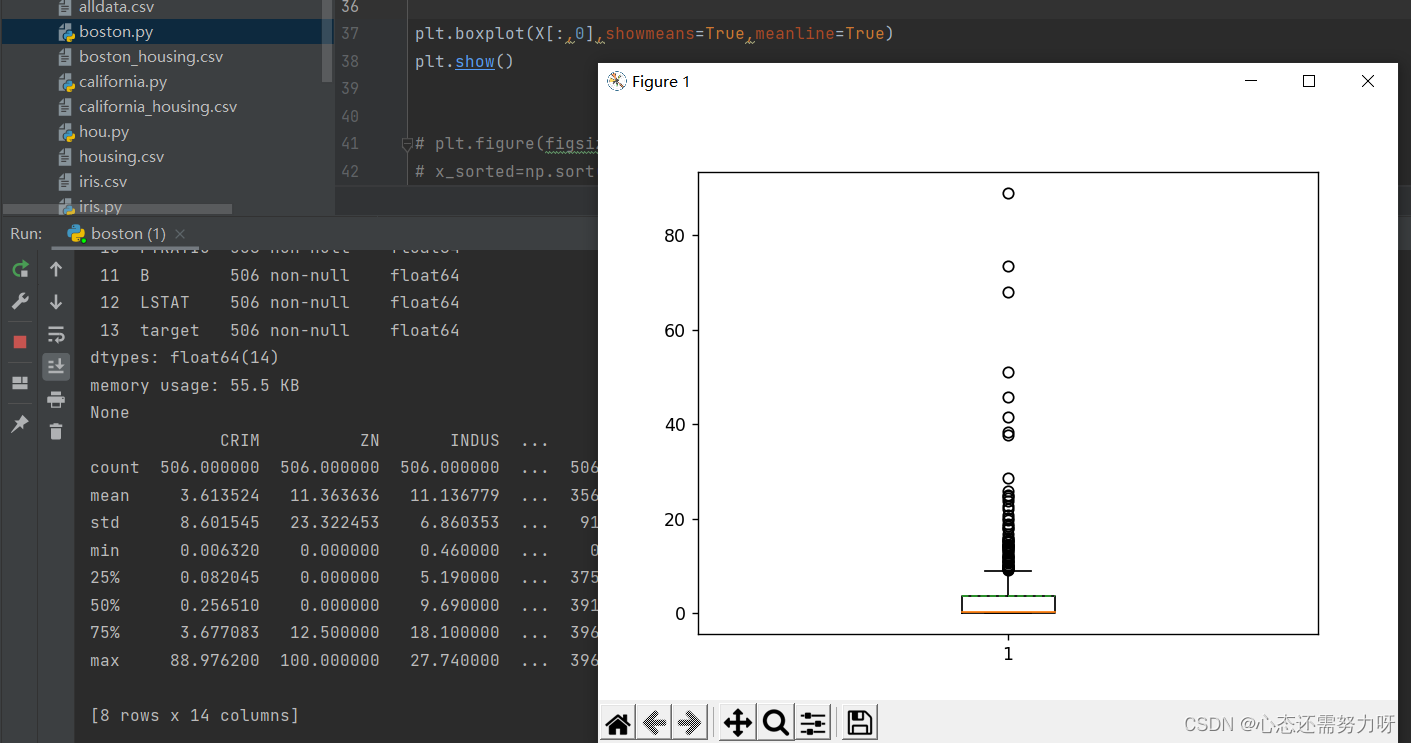
 分析：第一个特征的孤立点很多，在均值和中位数分析时也是一样，偏离性严重。

2.7 对所有特征画盒图（箱线图），检查孤立点（离群点）

代码：

plt.figure(figsize=(15, 15))
#对所有特征（收入中位数）画盒图（箱线图）
for i in range(X.shape[1]):
    plt.subplot(4,4,i+1)
    plt.boxplot(X[:,i],showmeans = True ,meanline = True)
    #x，y坐标轴标签
    plt.xlabel(housing['feature_names'][i])
plt.subplot(4,4,14)
#绘制直方图
plt.boxplot(y, showmeans = True ,meanline = True)
#x，y坐标轴标签
plt.xlabel('target')
plt.show()

效果图：

 分析：也可看出大部分特征没有离群点，只有个别特征存在离群点。也可从每个特征的均值和中位数中看出来。

2.8 对第一个特征排序后画散点图

代码：

x_sorted=np.sort(df.iloc[:,0].values)
# 画散点图
plt.scatter([i for i in range(X.shape[0])],x_sorted)
# 画x,y坐标轴标签
plt.xlabel('Count')
plt.ylabel('sorted'+housing['feature_names'][0])
plt.show()

效果图：

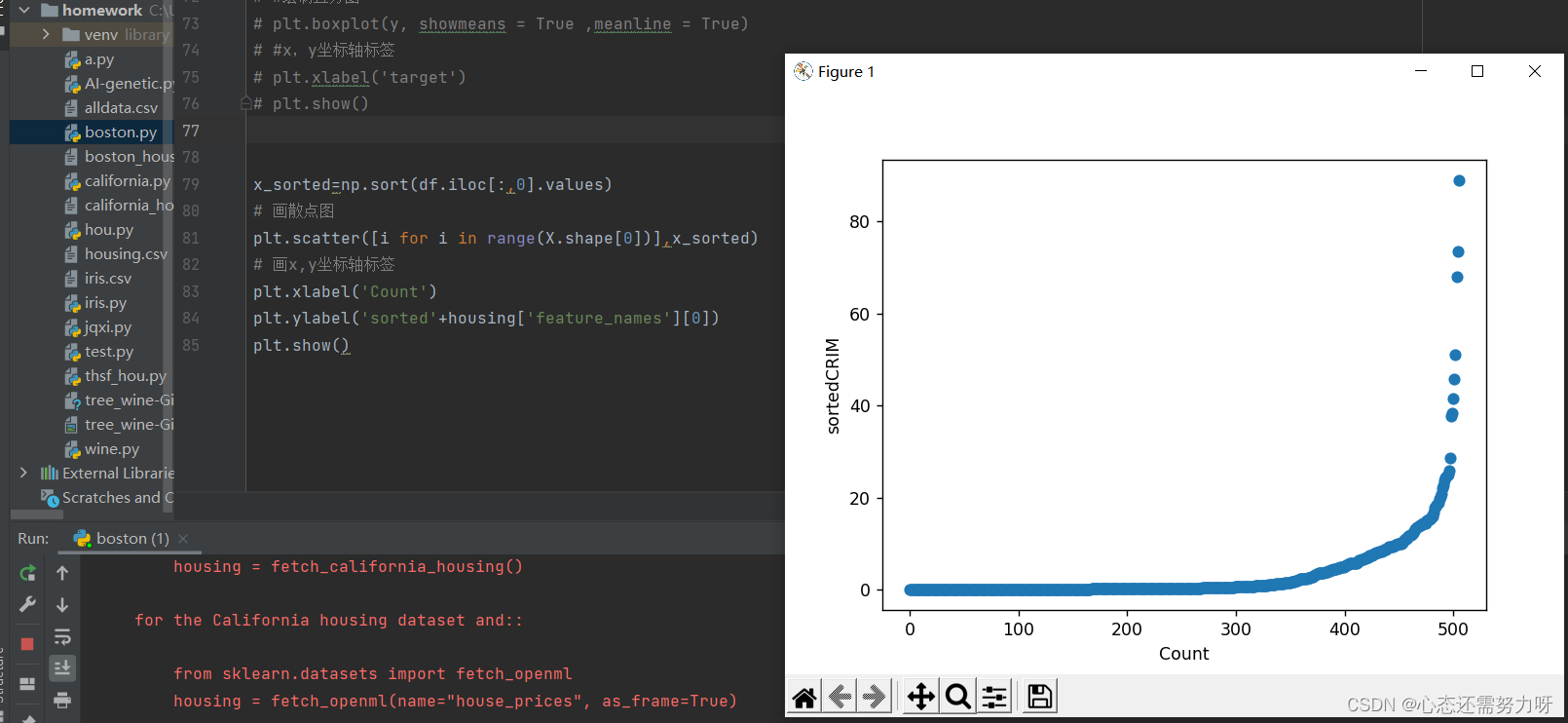
 分析：从人均犯罪率来看，大部分犯罪率都几乎为0，也有些犯罪率高达80%以上。

2.9 对第一个特征画分位数图

代码：

x_sorted=np.sort(df.iloc[:,0].values)
# 画散点图
plt.scatter([i for i in range(X.shape[0])],x_sorted)
# 画中位数点
plt.scatter([round(X.shape[0]/4),round(X.shape[0]/2),round(X.shape[0]*3/4)],
           [np.quantile(x_sorted,0.25),np.quantile(x_sorted,0.5),np.quantile(x_sorted,0.75)],color='red')
# 画x,y坐标轴标签
plt.xlabel('Count')
plt.ylabel('sorted'+housing['feature_names'][0])
plt.show()

效果图：

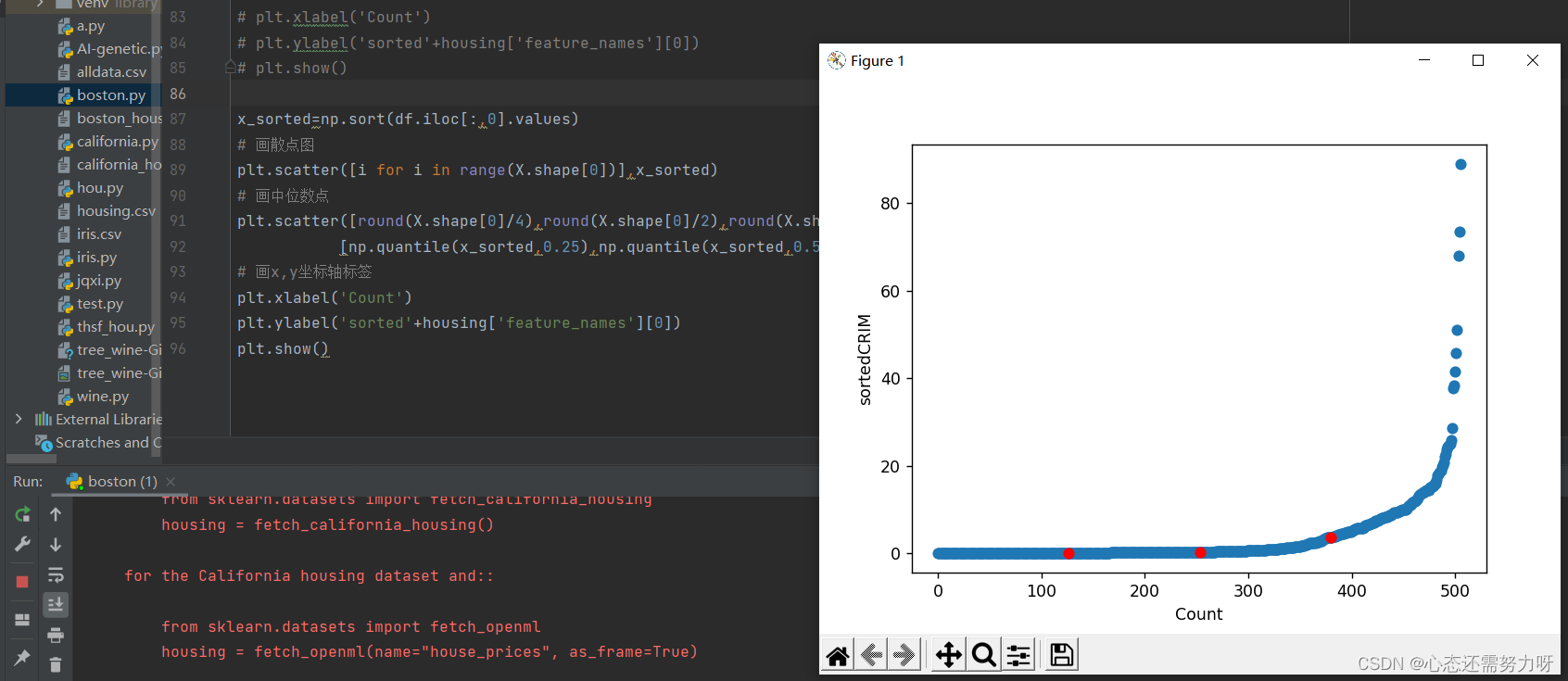
 分析：从图可看出75%的人群犯罪率几乎为0，25%的人群犯罪率比较高。

2.10 对所有特征画分位数图

代码：

plt.figure(figsize=(10, 10))
for j in range(X.shape[1]):

    # 对第一个特征（收入中位数）数据排序
    x_sorted=np.sort(df.iloc[:,j].values)
    plt.subplot(4,4,j+1)
    # 画散点图
    plt.scatter([i for i in range(X.shape[0])],x_sorted)
    # 画中位数点
    plt.scatter([round(X.shape[0]/4),round(X.shape[0]/2),round(X.shape[0]*3/4)],
                [np.quantile(x_sorted,0.25),np.quantile(x_sorted,0.5),np.quantile(x_sorted,0.75)],color='red')
    # 画x,y坐标轴标签
    plt.xlabel('Count')
    plt.ylabel('sorted'+housing['feature_names'][j])
plt.subplot(4,4,13)
plt.show()

效果图：

 分析：从图中可分析出每个特征的趋势和占比情况。

2.11 使用线性回归方法拟合第一个特征

代码：

X_list=[i for i in range(X.shape[0])]
X_array=np.array(X_list)
# 转换为矩阵
X_reshape=X_array.reshape(X.shape[0],1)
# 排序
x_sorted=np.sort(df.iloc[:,0].values)
from sklearn import linear_model
linear=linear_model.LinearRegression()
# 进行线性回归拟合
linear.fit(X_reshape,x_sorted)
# 对训练结果做拟合度评分
print("training score: ",linear.score(X_reshape,x_sorted))
plt.scatter(X_list,x_sorted)

y_predict=linear.predict(X_reshape)
plt.plot(X_reshape,y_predict,color='red')
plt.show()

效果图：

 分析：使用线性回归拟合第一个特征得分为33.9%，拟合度不高

2.12 使用局部回归（Loess）曲线（用一条曲线拟合散点图）方法拟合第一个特征数据

代码：

X_list=[i for i in range(X.shape[0])]
X_array=np.array(X_list)
# 转换为矩阵
X_reshape=X_array.reshape(X.shape[0],1)
# 排序
x_sorted=np.sort(df.iloc[:,0].values)
from sklearn import linear_model
# linear=linear_model.LinearRegression()
linear=linear_model.Lasso(fit_intercept=False)
# 进行Lasso局部回归拟合
linear.fit(X_reshape,x_sorted)
# 对训练结果做拟合度评分
print("training score: ",linear.score(X_reshape,x_sorted))
plt.scatter(X_list,x_sorted)

y_predict=linear.predict(X_reshape)
plt.plot(X_reshape,y_predict,color='red')
plt.show()

效果图：

分析：使用局部回归曲线拟合第一个特征得分为25.3%，拟合度也不高。

2.13 对第三个特征分两段画分位数-分位数图

代码：

import numpy as np
import matplotlib.pyplot as plt
plt.figure(figsize=(5,5))

df_new1=df[df['INDUS']<=df['INDUS'].mean()]
df_new2=df[df['INDUS']>df['INDUS'].mean()]

part1=np.sort(df_new1.iloc[:,0].values)[:df_new2['INDUS'].count()]
part2=np.sort(df_new2.iloc[:,0].values)[:df_new2['INDUS'].count()]

plt.xlim(part2[0],part2[-1])
plt.ylim(part2[0],part2[-1])
plt.plot([part2[0],part2[-1]],[part2[0],part2[-1]])

plt.scatter(part1,part2)
plt.scatter([np.quantile(part1,0.25),np.quantile(part1,0.5),np.quantile(part1,0.75)],
            [np.quantile(part2,0.25),np.quantile(part2,0.5),np.quantile(part2,0.75)],color='red')
plt.show()

效果图：

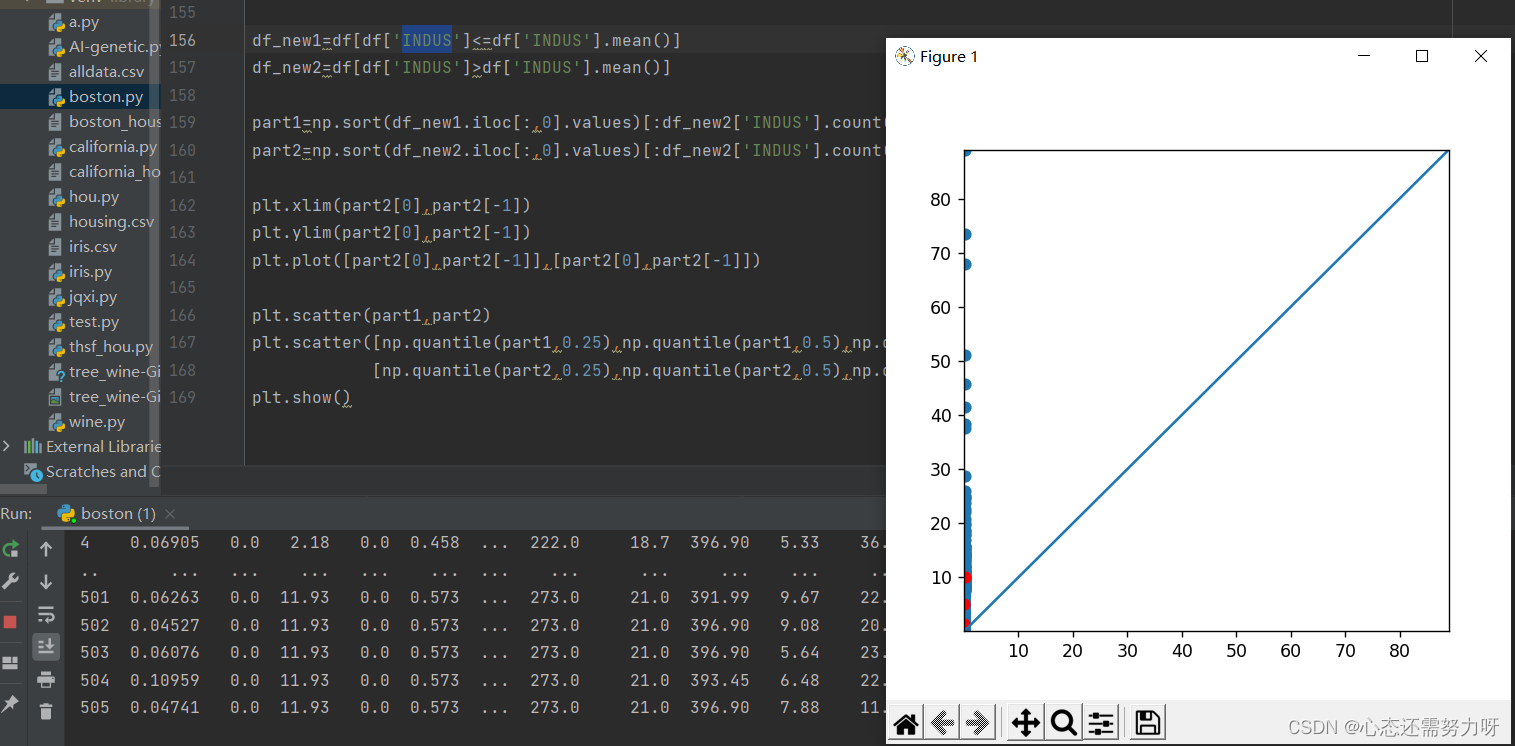
 分析：通过分位数-分位数图可发现都在其上方，人均犯罪率75%的人群在10%以下，有25%的人群犯罪率在10%以上。

2.14 画直方图，查看各个特征的分布和数据倾斜情况

代码：

plt.hist(X[:,0],edgecolor='k')
plt.show()

效果图：

 分析：从直方图也可看出上述的情况。人均犯罪率为0的居多数。也符合现实生活，但该城市的犯罪率也是比较高的。

2.15 对所有特征画直方图，查看数据的分布和数据倾斜情况

代码：

plt.figure(figsize=(10, 10))
for i in range(X.shape[1]):
    plt.subplot(4,4,i+1)
    plt.hist(X[:,i],edgecolor='k')
plt.subplot(4,4,14)
plt.hist(y,edgecolor='k')
plt.show()

效果图：

 

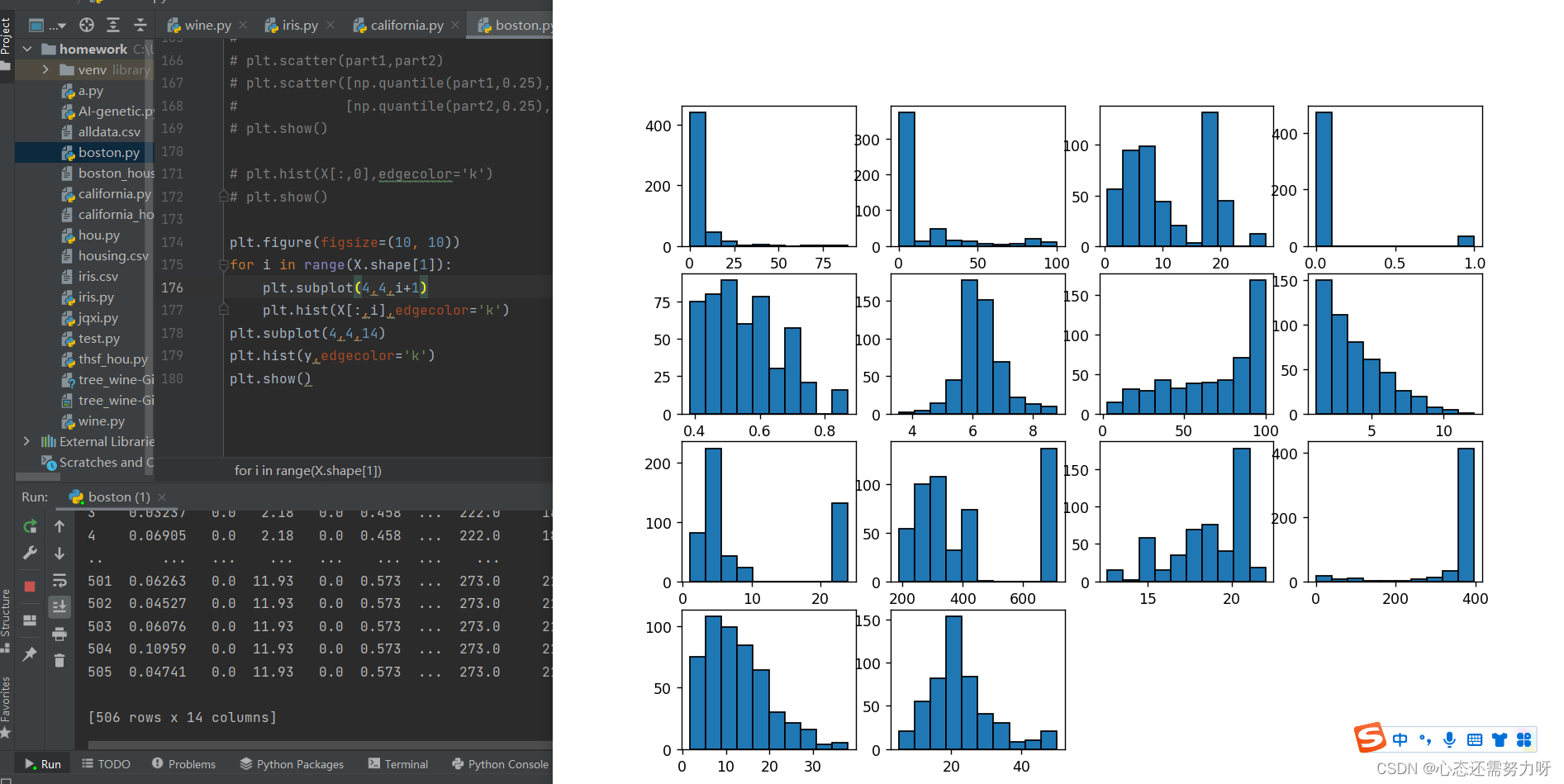
2.16 寻找所有特征之间的相关性并找出相关性大于 0.7 的特征对，做特征规约

代码：

for column in df.columns:
    correlations_data=df.corr()[column].sort_values()
    for key in correlations_data.keys():
        if key != column and abs(correlations_data[key]) >= 0.7:
            print('%s vs %s:' %(column,key),correlations_data[key])

效果图：

 分析：各个特征之间相关性大于0.7的数量比较多，我们在选择特征时最好是特征之间的相关性小于0.7的，这样我们才能很好的对数据进行分析，减少不必要的特征，运算时减少时间。

三、波士顿房价数据进行模拟训练（切分数据集7:3）

3.1 将数据集按7:3的比例切分为训练集和测试集，对全部特征（不切片）使用线性回归算法进行训练，显示训练集拟合度和测试集拟合度

代码：

X_train,X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
print('y_train = ', y_train)
print('y_test = ', y_test)

#线性回归
from sklearn import linear_model
model = linear_model.LinearRegression()
# model.fit(wine_X_train,wine_y_train)

# 模型训练及评估
model.fit(X_train,y_train)
print('\nTrain score:',model.score(X_train,y_train))
print('Test score:',model.score(X_test,y_test))

效果图：

 

3.2 对数据集进行按列归一化操作，使用梯度下降算法进行训练，显示训练集拟合度和测试集拟合度

代码：

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

# 数据预处理，按列归一化
X_train=preprocessing.scale(X_train)
X_test=preprocessing.scale(X_test)

# 线性回归之梯度下降法
from sklearn import linear_model
model=linear_model.SGDRegressor()
# 模型训练及评估
model.fit(X_train,y_train)
print('\nTrain score:',model.score(X_train,y_train))
print('Test score:',model.score(X_test,y_test))

效果图：

 

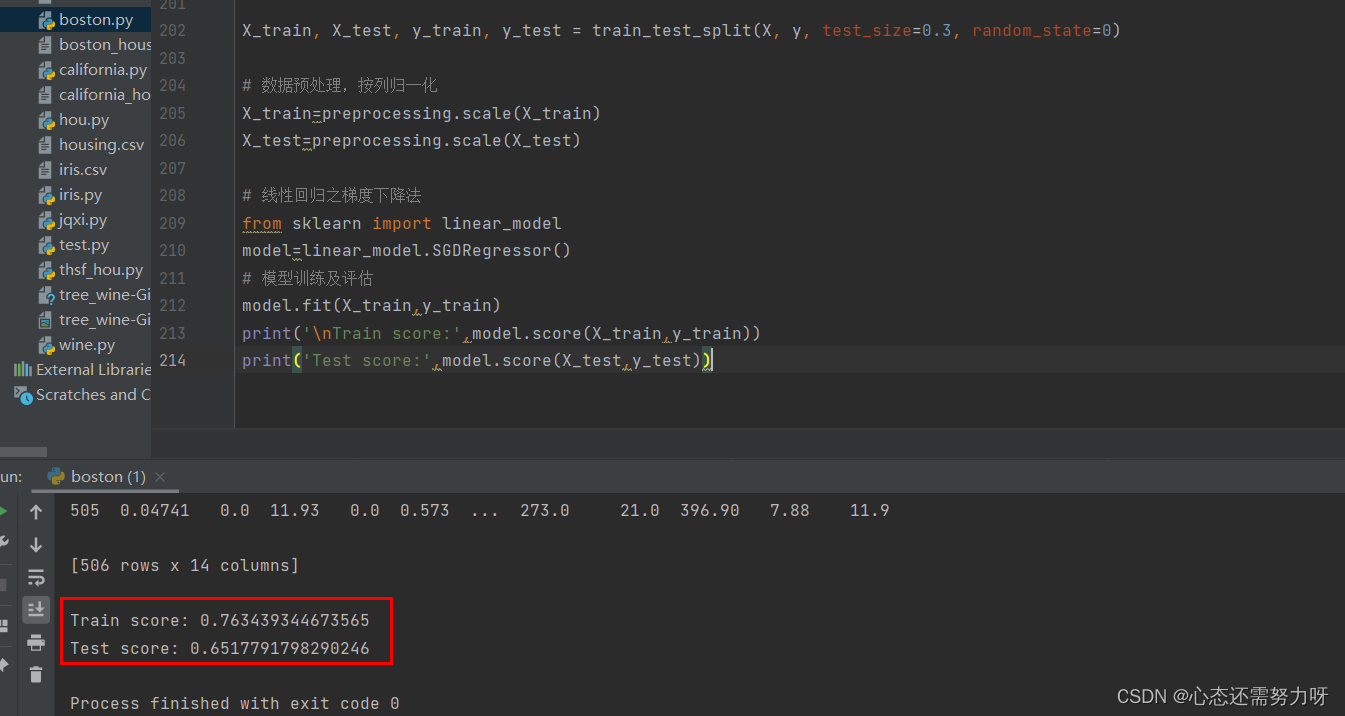
3.3 将随机森林算法用于回归问题：将波士顿房价数据集按7:3切分为训练集和测试集，使用随机森林回归器进行训练，显示训练集准确度和测试集准确度

代码：

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor

model = RandomForestRegressor()

# 训练评估
model.fit(X_train,y_train)
print('Train score:%f' % (model.score(X_train,y_train)))
print('Test score:%f' % (model.score(X_test,y_test)))

效果图：

 

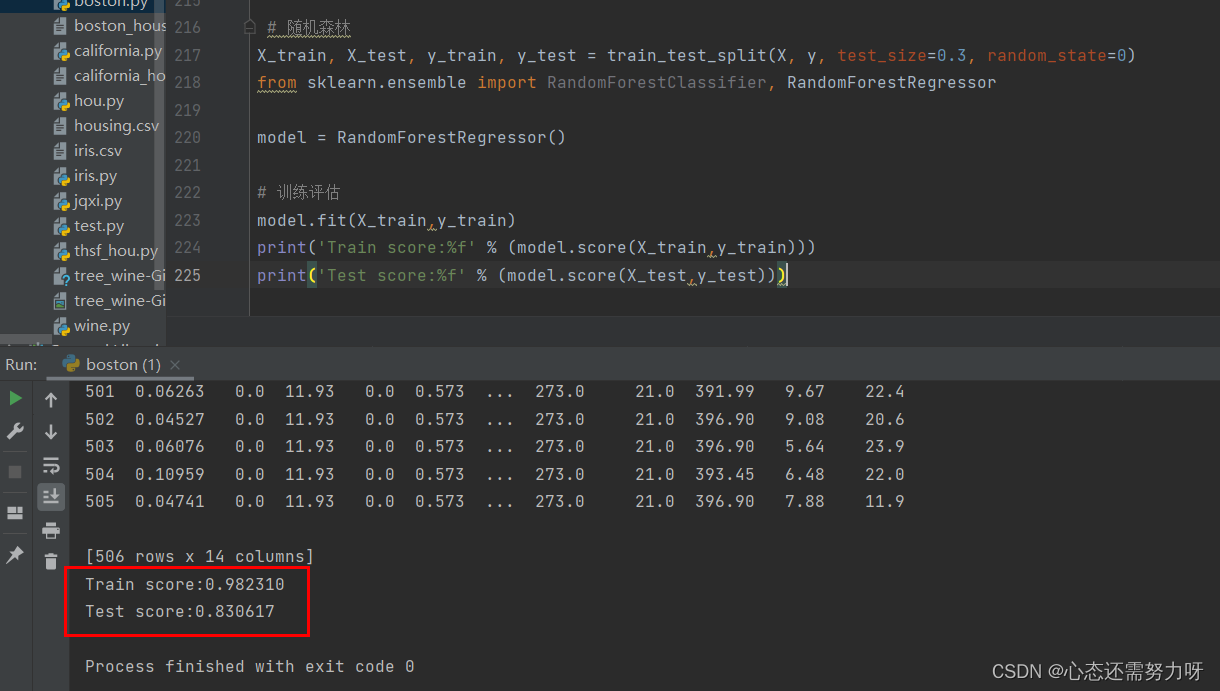
3.4 将GBDT算法用于回归问题：将波士顿房价数据集按7:3切分为训练集和测试集，使用GBDT回归器进行训练，显示训练集准确度和测试集准确度

代码：

housing_X=preprocessing.scale(X)
X_train, X_test, y_train, y_test = train_test_split(housing_X, y, test_size=0.3, random_state=0)
# GBDT算法
from sklearn.ensemble import GradientBoostingRegressor
model=GradientBoostingRegressor(random_state=3)

# 模型训练及评估
model.fit(X_train,y_train)
print('Train score:%f' % (model.score(X_train,y_train)))
print('Test score:%f' % (model.score(X_test,y_test)))

效果图：

 

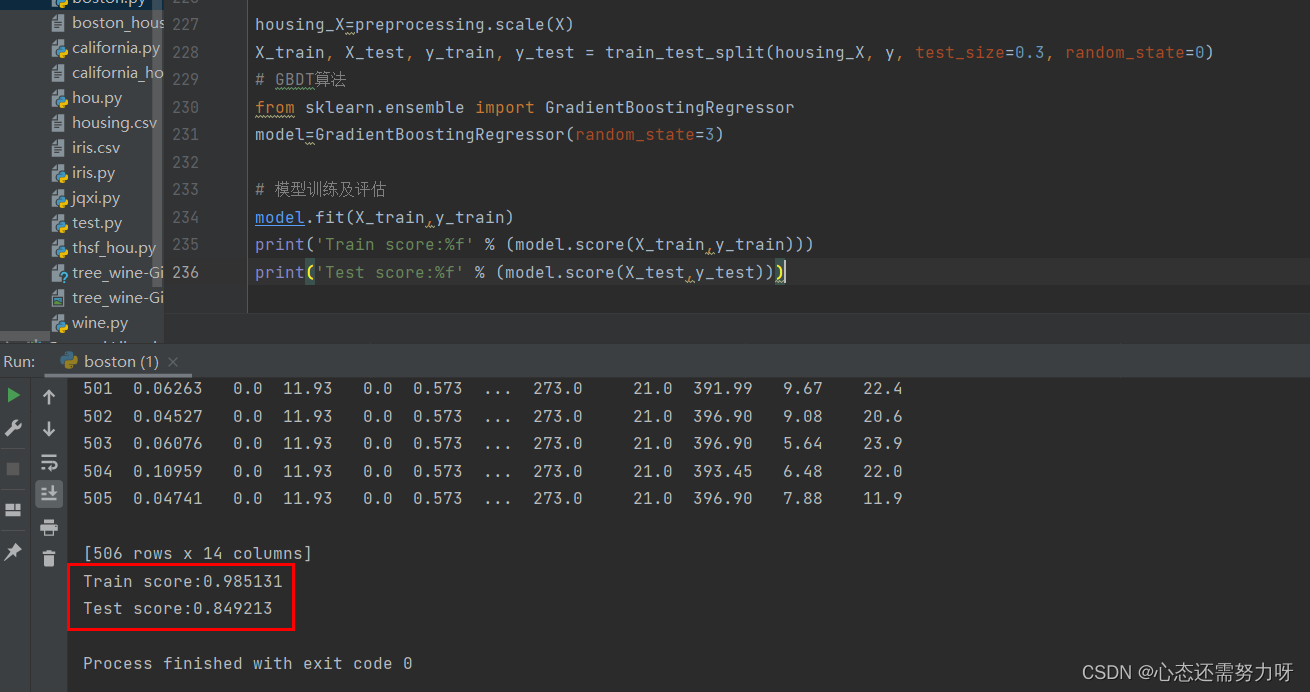
3.5 将岭回归算法用于回归问题：将波士顿房价数据集按7:3切分为训练集和测试集，使用岭回归算法进行训练，显示训练集拟合度和测试集拟合度；导入sklearn的MSE和MAE方法计算均方误差和平均绝对误差评价指标

代码：

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

from sklearn import linear_model
model=linear_model.Ridge(alpha=0.3)

model.fit(X_train,y_train)
print("\ntraining score: ",model.score(X_train,y_train))
print("Test score: ",model.score(X_test,y_test))

y_predict=model.predict(X_test)
print("均方误差为： ",mean_squared_error(y_test,y_predict))
print("平均绝对误差为：",mean_absolute_error(y_test,y_predict))
print("R_squared：",r2_score(y_test,y_predict))

效果图：

 

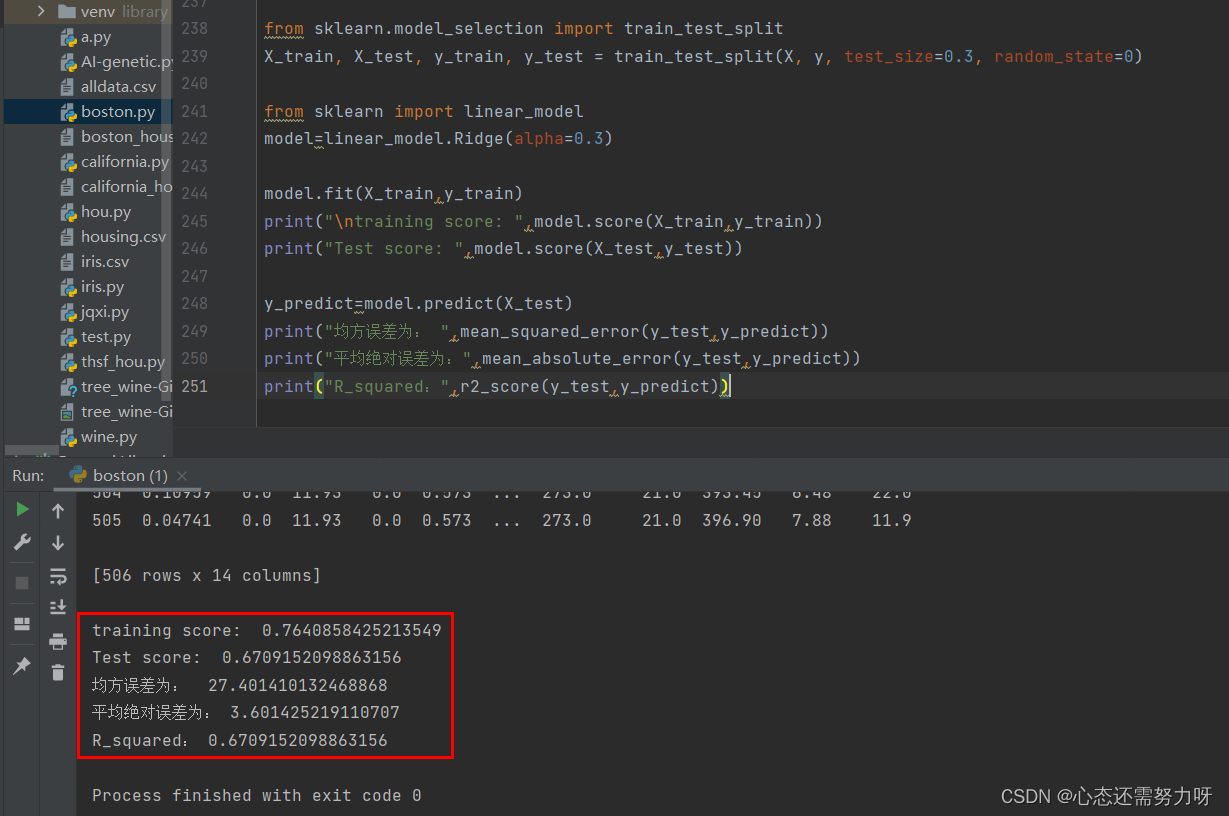
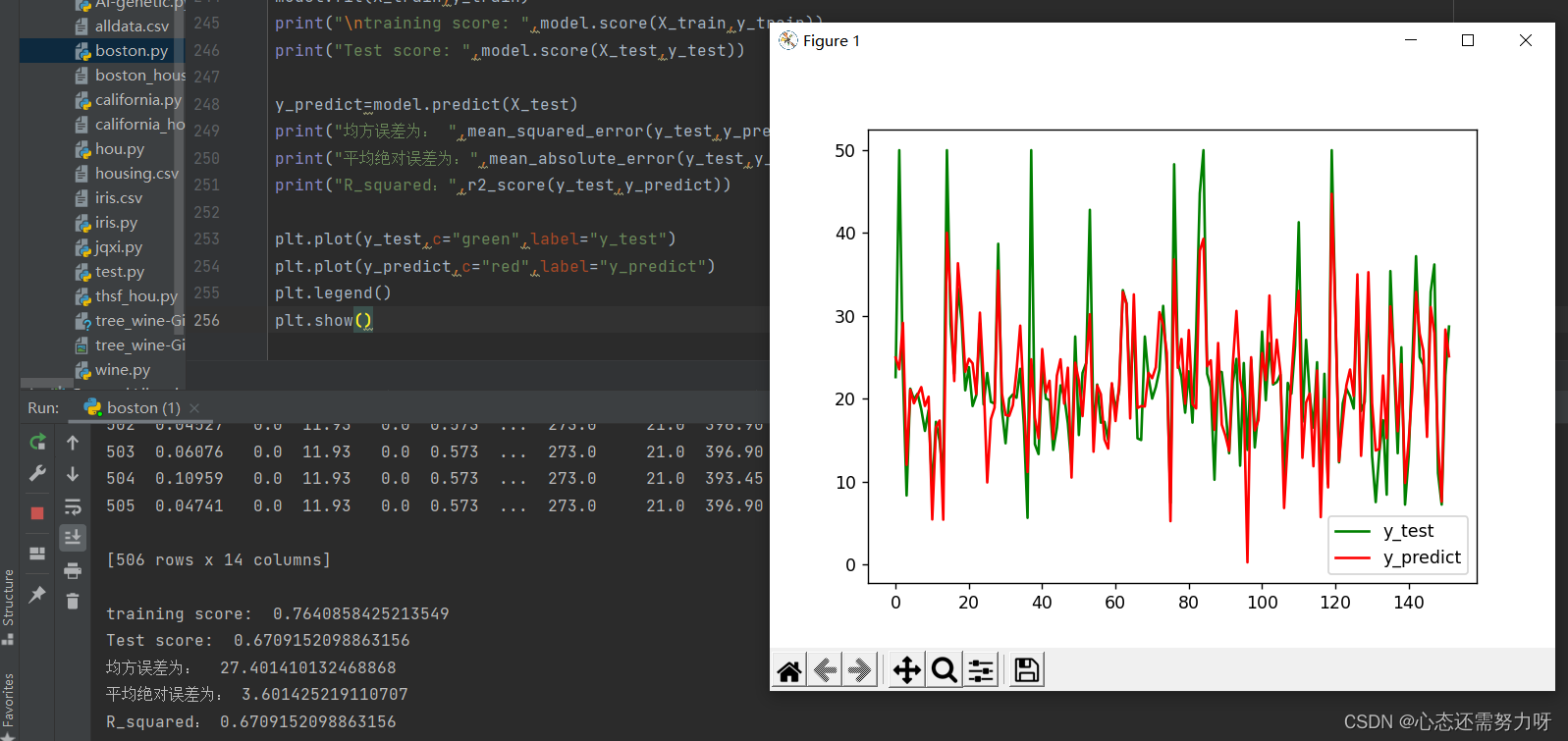
3.6 测试值与预测值之间的差距

代码：

plt.plot(y_test,c="green",label="y_test")
plt.plot(y_predict,c="red",label="y_predict")
plt.legend()
plt.show()

效果图：

---

 总结

到这里就把我对波士顿数据集进行数据预处理和模型训练的代码和相关的效果图已经展示给大家，如果想学数据预处理的可以用python的scikit-learn包下导入就可跟着做做。还有红酒数据集、鸢尾花数据集、加州房价数据集等，这些都可以拿来练手。其中加州房价的数据比较的多，上万条数据，大家做熟练的话这个数据集是非常不错练手的。