40.组合总和II
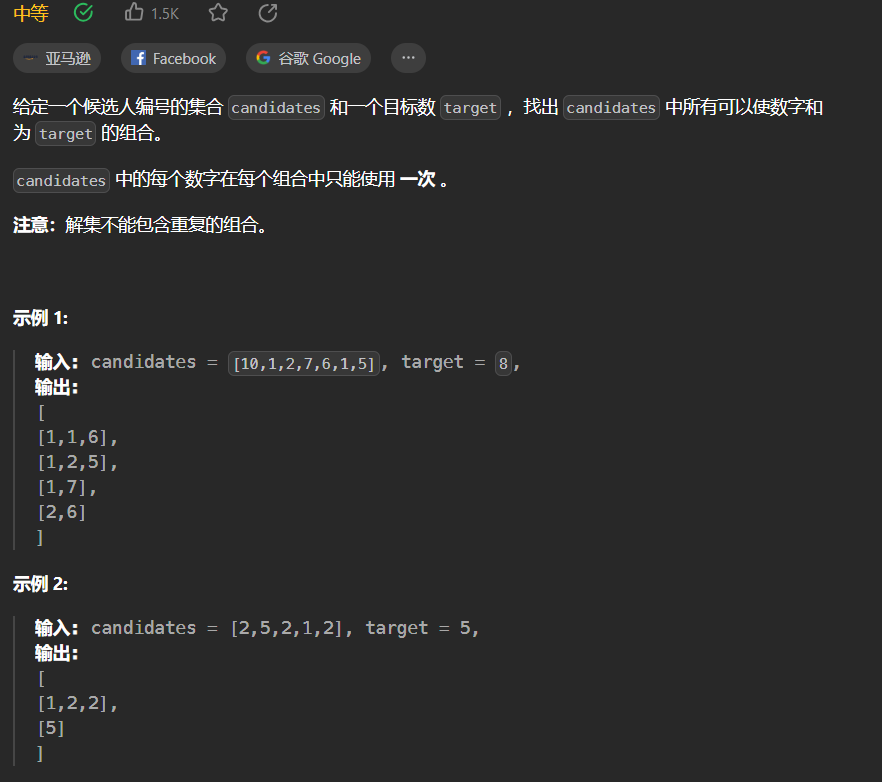
本题详解:回溯算法
class Solution {
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
int len = candidates.length;
List<List<Integer>> res = new ArrayList<>();
if (len == 0) {
return res;
}
// 关键步骤
Arrays.sort(candidates);
Deque<Integer> path = new ArrayDeque<>(len);
dfs(candidates, len, 0, target, path, res);
return res;
}
/**
* @param candidates 候选数组
* @param len 冗余变量
* @param begin 从候选数组的 begin 位置开始搜索
* @param target 表示剩余,这个值一开始等于 target,基于题目中说明的"所有数字(包括目标数)都是正整数"这个条件
* @param path 从根结点到叶子结点的路径
* @param res
*/
private void dfs(int[] candidates, int len, int begin, int target, Deque<Integer> path, List<List<Integer>> res) {
if (target == 0) {
res.add(new ArrayList<>(path));
return;
}
for (int i = begin; i < len; i++) {
// 大剪枝:减去 candidates[i] 小于 0,减去后面的 candidates[i + 1]、candidates[i + 2] 肯定也小于 0,因此用 break
if (target - candidates[i] < 0) {
break;
}
// 小剪枝:同一层相同数值的结点,从第 2 个开始,候选数更少,结果一定发生重复,因此跳过,用 continue
if (i > begin && candidates[i] == candidates[i - 1]) {
continue;
}
path.addLast(candidates[i]);
// 因为元素不可以重复使用,这里递归传递下去的是 i + 1 而不是 i
dfs(candidates, len, i + 1, target - candidates[i], path, res);
path.removeLast();
}
}
}




![[计算机网络实验]头歌 实验二 以太网帧、IP报文分析(含部分分析)](https://img-blog.csdnimg.cn/4a40c35e26b04992b33bf02651dd6a79.png)