文章目录
- 前言
- 一、什么是PBR
- 二、什么是PBS
- 在这里插入图片描述
- 三、PBS的核心理论
- 1、物质的光学特性(Substance Optical Properties)
- 2、微平面理论(Microfacet Theory)
- 3、能量守恒(Energy Conservation)
- 4、菲涅尔反射(Fresnel Reflection)
- 5、线性空间光照(Linear Space Lighting)
前言
Unity中Shader的PBR的基础知识与理论
一、什么是PBR
-
PBR(Physically Based Rendering),中文译为基于物理的渲染
-
PBR是一种渲染方式,是使用基于物理原理和微微、平面理论的光照模型,以及使用从现实中测量的表面参数来准确表示真实世界材质的渲染理念
-
PBR是一系列技术的集合,包含GI、PBS等。
PBS 是 PBR 的核心
二、什么是PBS
-
PBS(Physically Based Shadering),中文译为基于物理的着色。
-
PBS是为了对光和材质之间进行更加真实的建模,实质上讲基于物理的渲染本质就是PBS
-
Unity中的PBS分为 Standard 和 Standard(Specular Setup)
三、PBS的核心理论
1、物质的光学特性(Substance Optical Properties)
现实世界中的物质根据导电性可分为三大类:绝缘体、半导体、导体
渲染领域中大多分为两大类:导体(金属)、绝缘体(非金属)

金属(导体)特性:
-
金属具有很高的反射率(>=0.5)
-
金属会立即吸收任何折射光,因此金属不会出现 任何 次表面散射 和 透明效果
-
金属的所有可见颜色都来自反射
-
不同金属反射的光是不一样的,而非金属反射都光都一样

非金属(绝缘体)特性:
- 非金属具有很低的反射率(<=0.06)
- 非金属会产生高光反射与漫反射现象
- 非金属的高光反射为 单色 / 灰色

2、微平面理论(Microfacet Theory)
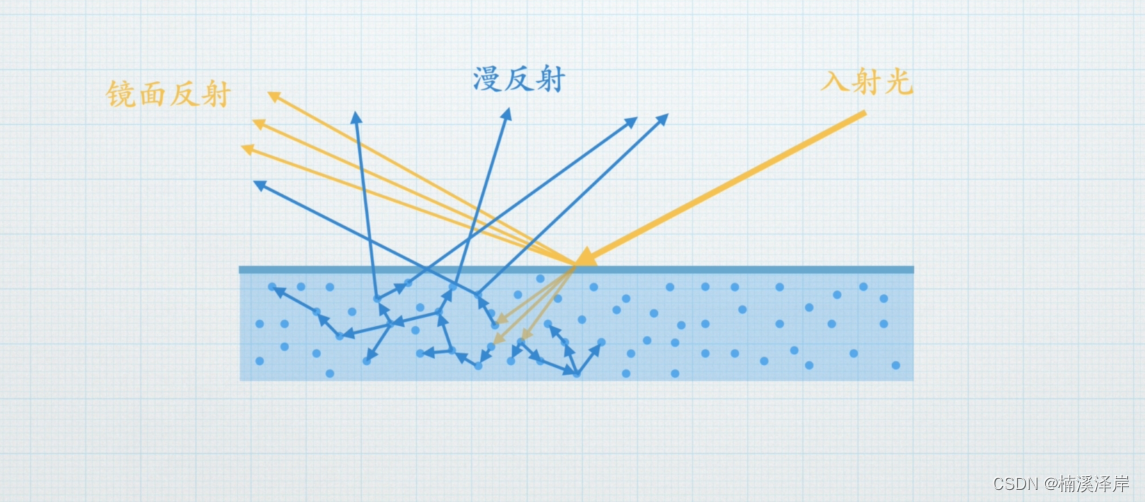
现实世界的表面大多都不是光学光滑的,这种微观几何上的变化会导致每个表面点对光由不同的反射和折射。
所以基于物理渲染的PBS技术都是基于微平面理论的,它假想任何平面都是由微平面组成的,根据这些微平面粗糙程度的不同,采用粗糙度贴图或者高光度贴图来进行表示

- 一个平面越是粗糙,这个平面上的微平面排列就越是混乱

- 一个平面越是平滑,这个平面上的微平面排列就越是整齐
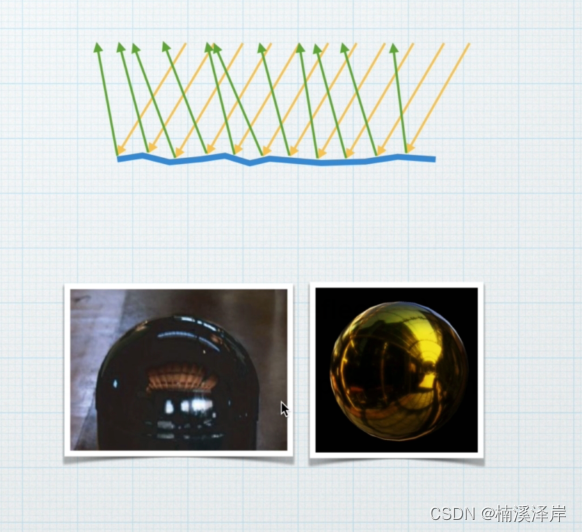
3、能量守恒(Energy Conservation)
-
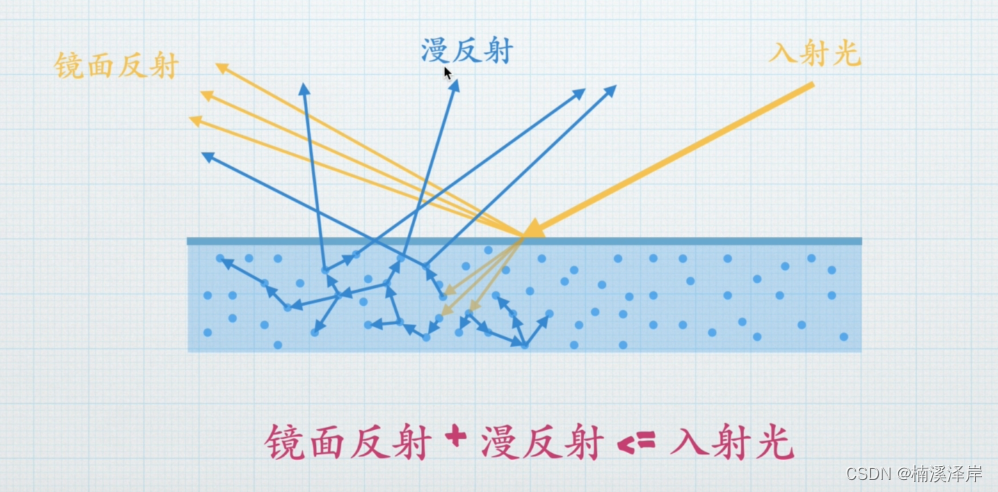
出射光线的能量永远不能超过入射光线的能量(自发光体除外)
-
随着粗糙度的上升,镜面反射区域的面积会增加,基于能量守恒,故镜面反射的亮度则会降低
4、菲涅尔反射(Fresnel Reflection)
-
菲涅尔效应是一种表示看到光线的反射率与视角相关的现象,也就是光源入射方向与平面法线方向夹角的对应关系。
-
夹角越大,反射越大,亮度也就越大,反之夹角越小,反射就越小,亮度也就越小
而这效应中的反射率就被称为菲涅尔反射

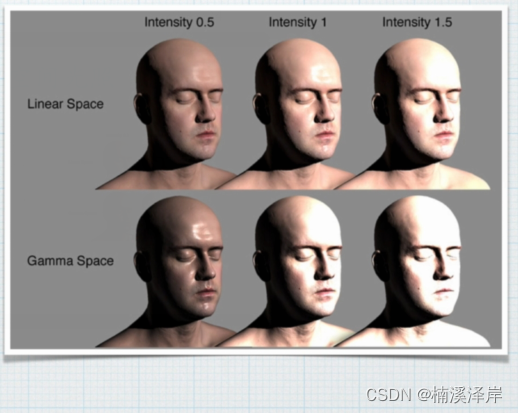
5、线性空间光照(Linear Space Lighting)
- 为了保证光照渲染的正确性,所以最好是在线性空间中进行操作与计算,这样才能尽最大的还原现实世界中光与物质的交互