C++刷题 – 二分查找
文章目录
- C++刷题 -- 二分查找
- 一、原理
- 二、例题
- 1.二分查找
- 2.使用二分查找确定target左右边界
- 3.x的平方根
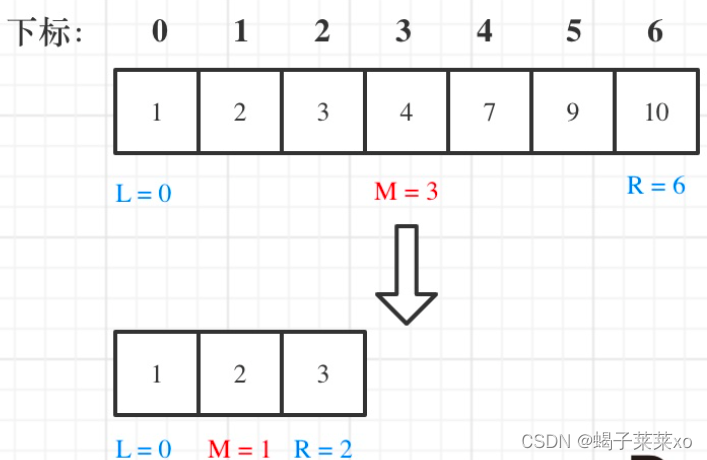
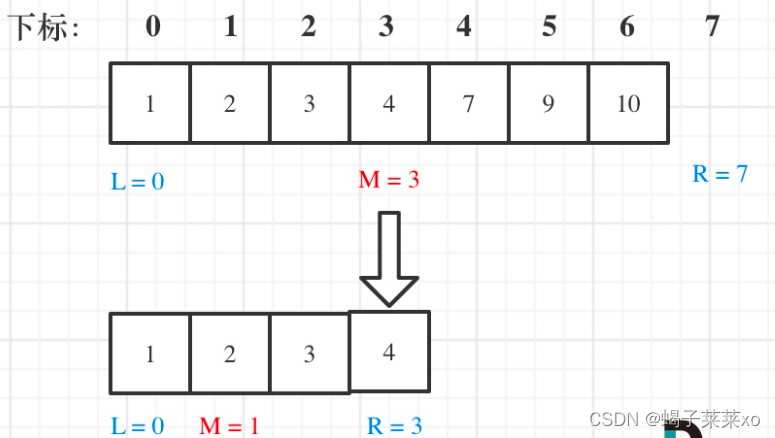
一、原理
条件:数组为有序数组,数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的;
- 第一种写法:

class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
while (left <= right) { // 当left==right,区间[left, right]依然有效,所以用 <=
int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
if (nums[middle] > target) {
right = middle - 1; // target 在左区间,所以[left, middle - 1]
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,所以[middle + 1, right]
} else { // nums[middle] == target
return middle; // 数组中找到目标值,直接返回下标
}
}
// 未找到目标值
return -1;
}
};
- 第二种写法:

class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size(); // 定义target在左闭右开的区间里,即:[left, right)
while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
int middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle; // target 在左区间,在[left, middle)中
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,在[middle + 1, right)中
} else { // nums[middle] == target
return middle; // 数组中找到目标值,直接返回下标
}
}
// 未找到目标值
return -1;
}
};
二、例题
1.二分查找
https://leetcode.cn/problems/binary-search/description/
2.使用二分查找确定target左右边界
https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/
- 该题目的要点在于非递减数组(升序,但是有可能有重复数字)中寻找target的左右边界,target可能有多个重复值的情况;
- 时间复杂度需要是O(log N),表明需要使用二分查找确定左右边界,不能采用遍历方法确定边界;
- 先确定情况:
- target不再nums区间内;
- target在nums区间内,但是nums中没有target;
- nums中有target;
使用二分查找确定边界的原理:
二分查找在没有查找到target的时候,target是在最终的(left, right)这个区间之内的,可以使用这个原理来分别找出左右边界;
- 确定右边界

当nums[mid]的值小于等于target的时候,选择更新right_border,right_border需要跟着left更新,因为无论是否找到target,最终left一定会指向nums中大于target的数中最小的那个数,就是target的有边界(开区间); - 左边界同理;
特殊情况:
- nums为{2, 2},target为3,最终左右边界输出值为(-2, 2),之间的差值大于1,应该输出左右边界,但是target却不在nums中;
解决方案:直接在最外面加一个判断target是否属于nums区间的条件;
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
vector<int> res;
int tar_l = leftBorder(nums, target);
int tar_r = rightBorder(nums, target);
cout << tar_l << " " << tar_r << endl;
if(nums.empty() || (target < nums[0] || target > nums[nums.size() - 1]))
{
//target不在nums范围
res.push_back(-1);
res.push_back(-1);
}
else if(tar_r - tar_l > 1)
{
//target存在于nums中
res.push_back(tar_l + 1);
res.push_back(tar_r - 1);
}
else
{
//target不存在于nums中
res.push_back(-1);
res.push_back(-1);
}
return res;
}
//寻找右边界 -- target右边的一个位置
int rightBorder(vector<int>& nums, int target)
{
int right_border = -2;
int left = 0, right = nums.size() - 1;
//进行二分查找
while(left <= right)
{
int mid = left + ((right - left) / 2);
if(nums[mid] > target)//不断缩小右边界
{
right = mid - 1;
}
else
{
//缩小左边界
//且当找到target时,left继续向右,目的是找到最右边target的位置
left = mid + 1;
right_border = left;
//left最终指向的会是nums中大于target的最小数
}
}
return right_border;
}
//寻找左边界
int leftBorder(vector<int>& nums, int target)
{
int left_border = -2;
int left = 0, right = nums.size() - 1;
//进行二分查找
while(left <= right)
{
int mid = left + ((right - left) / 2);
if(nums[mid] < target)//不断缩小左边界
{
left = mid + 1;
}
else
{
//缩小右边界
//且当找到target时,right继续向右,目的是找到最左边target的位置
right = mid - 1;
left_border = right;
//right最终指向的会是nums中小于target的最大数
}
}
return left_border;
}
};
3.x的平方根
https://leetcode.cn/problems/sqrtx/submissions/483798269/
从题目的要求和示例我们可以看出,这其实是一个查找整数的问题,并且这个整数是有范围的。
- 如果这个整数的平方 恰好等于 输入整数,那么我们就找到了这个整数;
- 如果这个整数的平方 严格大于 输入整数,那么这个整数肯定不是我们要找的那个数;
- 如果这个整数的平方 严格小于 输入整数,那么这个整数 可能 是我们要找的那个数(重点理解这句话)。
因此我们可以使用「二分查找」来查找这个整数,不断缩小范围去猜。
方法一:
- 猜的数平方以后大了就往小了猜;
- 猜的数平方以后恰恰好等于输入的数就找到了;
- 猜的数平方以后小了,可能猜的数就是,也可能不是。
class Solution {
public:
int mySqrt(int x) {
int min = 0, max = x;
int res = 0;
while(min <= max)
{
int mid = min + (max - min) / 2;
if((long long)mid * mid <= x) // 防止乘法溢出
{
// 目标结果的平方小于等于x,寻找出的就是范围内最大的满足平方<=x的数
min = mid + 1;
res = mid;
}
else
{
max = mid - 1;
}
}
return res;
}
};
方法二:
- 使用二分查找寻找边界,目标数其实就是左边界;
class Solution {
public:
int mySqrt(int x) {
int min = 0, max = x;
int res = 0;
//寻找左边界
while(min <= max)
{
int mid = min + ((max - min) / 2);
if((long long)mid * mid < x)
{
min = mid + 1;
}
else if((long long)mid * mid > x)
{
max = mid - 1;
res = max;
}
else
{
return mid;
}
}
return res;
}
};




![C# - Opencv应用(2) 之矩阵Mat使用[矩阵创建、图像显示、像素读取与赋值]](https://img-blog.csdnimg.cn/f4acf3b030754530a47f3b95ae2ffb0e.png)