目录
1、二叉树的概念及结构
2、二叉树的遍历概念
2.1 二叉树的前序遍历
2.2 二叉树的中序遍历
2.3 二叉树的后序遍历
2.4 二叉树的层序遍历
3、创建一颗二叉树
4、递归方法实现二叉树前、中、后遍历
4.1 实现前序遍历
4.2 实现中序遍历
4.3 实现后序遍历
5、求二叉树的结点总数
6、求二叉树叶子个数
7、求第k层结点总数
8、求二叉树的高度
9、从二叉树中查找值为x的结点
10、层序遍历
11、二叉树的销毁
12、测试功能
结语:
1、二叉树的概念及结构
二叉树是由根节点和一个左子树以及一个右子树构成,且每一个结点的孩子节点可以少于两个但是不能多于两个,每个结点都带有一个数据,作为结点的有效值。二叉树示意图如下:

从上图可以看出,位于根结点左半部分的称为左子树,位于根结点右半部分的称为右子树,二叉树的顺序不能颠倒。同时2既可以看出是根结点1的孩子结点,他也可以作为3的父母结点,因此2也可以看作是一个根结点。
因此二叉树通常都采用递归的方式来实现。
2、二叉树的遍历概念
在学习数组的时候,有一个最基本的概念就是遍历数组,数组的很多问题都是在遍历数组的基础上完成的。学习链表的时候,链表的很多操作也是在遍历链表的前提下实现的。因此,要对二叉树进行一系列的操作,也需要遍历二叉树。
二叉树的遍历一般采用递归的方式,对二叉树的每个结点进行相应操作。二叉树的遍历分为:前序遍历、中序遍历、后序遍历以及层序遍历。
2.1 二叉树的前序遍历
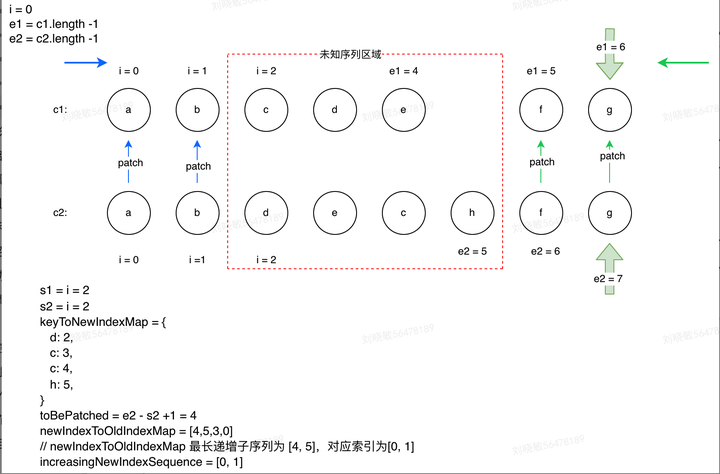
前序遍历的顺序:根、左子树、右子树。结构图如下:
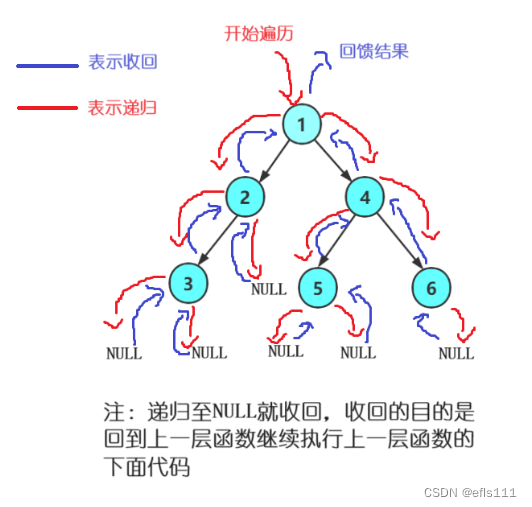
上图的二叉树前序遍历:123NNN45NN6NN(N表示NULL)。
前序遍历详解:1为根节点,因此从1开始遍历,2是1的左子树也就是遍历到2这个位置(前序遍历顺序:根-左子树-右子树),这时候会把2看成一棵树(2为根结点),然后逻辑又回到了根-左子树-右子树,3是2的左子树,因此下一个遍历的就是3,这时候又把3看成了一棵树(3为根结点),遍历3结点的左子树也就是NULL,当遍历当NULL的时候就开始“往上收回”,这时候3的左子树收回后就去遍历右子树,而这里3的右子树也是NULL因此也发生收回,最后的结果就是3结点遍历完成,同时表示结点2的左子树遍历完成,接下来就是遍历结点2的右子树,最后收回到根结点1(表示根结点1的左子树遍历完成)。接下来就是去遍历根结点1的右子树,遍历右子树的逻辑也是一样,把4看成根节点,继续根-左子树-右子树的逻辑。
2.2 二叉树的中序遍历
中序遍历的结构图与前序遍历的结构图相似,只是中序遍历的顺序不一样,中序遍历顺序为:左子树、根、右子树。
因此该二叉树的中序遍历的顺序为:N3N2N1N5N4N6N(N表示NULL)。
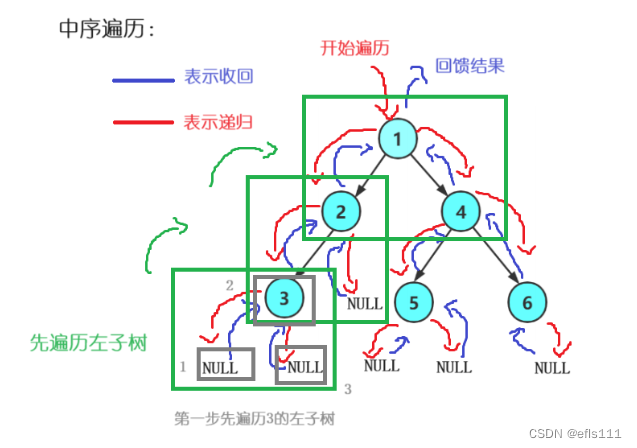
中序遍历详解:2可以看成是1的左子树,3可以看成是2的左子树,NULL是3的左子树。中序遍历的第一个是左子树,因此把3看成是一棵树并且从3入手,遍历3的左子树NULL,然后是根结点3,最后是3的右树NULL,所以顺序为N3N。接下来把3看成是2的左子树,逻辑一样为:左子树-根-右子树,3遍历完成代表2的左子树遍历完成,接下来是根结点2,然后是根结点2的右子树NULL,此时顺序为:N3N2N。2作为根结点遍历完成后,表示1的左子树遍历完成,接下来遍历的逻辑是根结点1-1的右子树,把4当成根结点执行同样的逻辑:左子树-根-右子树。
2.3 二叉树的后序遍历
接下来的后序遍历的顺序为:左子树、右子树、根。其逻辑与上述相似,只不过顺序做了调整。

该二叉树的后序遍历顺序为:NN3N2NN5NN641(N表示NULL)。
2.4 二叉树的层序遍历
层序遍历顾名思义就是一层一层、自上而下从左到右的遍历,首先从第一层也就是根结点开始,其次是第二层,并且从左边到右边的遍历,以此类推。
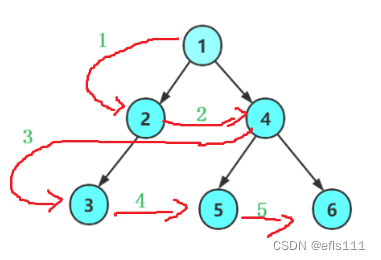
因此层序遍历的顺序为:1 2 4 3 5 6。
下面使用代码来实现二叉树及各个功能。
3、创建一颗二叉树
从二叉树的结构分析可以得出,创建二叉树要满足三个条件:有效数据、指向左孩子的指针,指向右孩子的指针。
创建二叉树代码如下:
typedef int TreeDataType;//int类型重定义
typedef struct TreeNode
{
TreeDataType data;
struct TreeNode* left;//指向左孩子指针
struct TreeNode* right;//指向右孩子指针
}TNode;
TNode* CreatTree()//创造二叉树
{
//创建结点
TNode* n1 = CreatTreeNode(1);
TNode* n2 = CreatTreeNode(2);
TNode* n3 = CreatTreeNode(3);
TNode* n4 = CreatTreeNode(4);
TNode* n5 = CreatTreeNode(5);
TNode* n6 = CreatTreeNode(6);
//TNode* n7 = CreatTreeNode(7);
//构建树结点之间的关系
n1->left = n2;
n1->right = n4;
n2->left = n3;
n4->left = n5;
n4->right = n6;
//n5->left = n7;
return n1;//返回该二叉树的根节点
}该二叉树的物理图:

4、递归方法实现二叉树前、中、后遍历
4.1 实现前序遍历
前序遍历代码如下:
void PreOrder(TNode* root)//前序遍历
{
if (root == NULL)
{
printf("N ");//当递归到NULL时打印并返回N
return;
}
printf("%d ", root->data);//打印根节点
PreOrder(root->left);//打印左子树
PreOrder(root->right);//打印右子树
}因为二叉树是由递归实现的,并且前序遍历的顺序为:根-左子树-右子树。进入函数PreOrder时如果结点root不是空结点,则可以将该结点看成根节点,按照前序遍历的逻辑打印该结点的值,然后继续遍历该结点的左子树,和右子树,当结果为NULL时就会跳出该函数。当结点3的函数走完了,就会收回至结点2的函数,说明结点2的左子树函数完成。
具体步骤图如下:
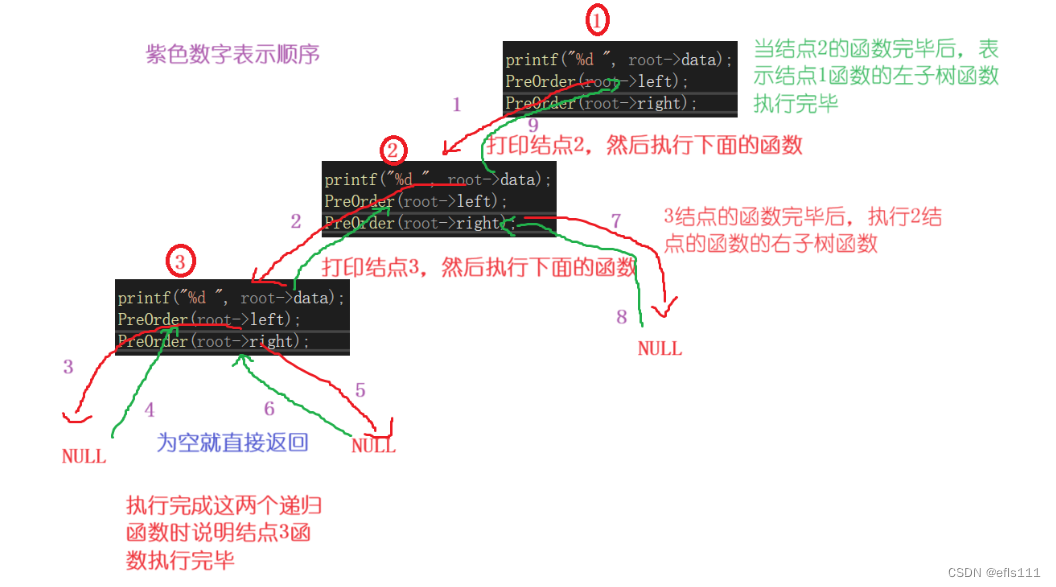
4.2 实现中序遍历
中序遍历的顺序与前序遍历顺序不一样,因此对前序遍历的代码稍作修改即可。
中序遍历代码如下:
void InOrder(TNode* root)//中序遍历
{
if (root == NULL)
{
printf("N ");
return;
}
//相比于前序遍历,把这两个语句的顺序交换了以下
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}可以发现,中序遍历中的打印根结点的代码与左子树代码只是做了简单的更替便可以实现中序遍历,交换后三个语句的顺序也刚好对应中序遍历的顺序:左子树-根-右子树。
4.3 实现后序遍历
经过上述的规律可以得出后序遍历的代码逻辑。
后序遍历代码如下:
void PostOrder(TNode* root)//后序遍历
{
if (root == NULL)
{
printf("N ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}5、求二叉树的结点总数
求二叉树结点的总数,第一步就是要遍历二叉树。因此采用的是递归的方式,因此每次函数调用返回的时候要返回当前结点的个数。
这里注意的点:当递归的函数返回一个值,是返回给上一层调用该函数的函数,如此层层返回最后返回给根结点函数。
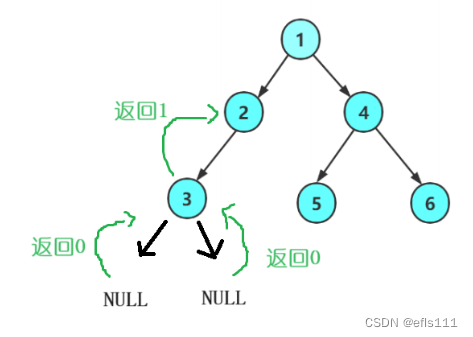
求二叉树结点总数代码如下:
int BinaryTreeSize(TNode* root)//结点个数
{
if (root == NULL)//为空返回0
return 0;
//递归左右子树
return BinaryTreeSize(root->left)
+ BinaryTreeSize(root->right) + 1;//若执行到此语句说明root不为空
//+1表示把当前的结点记录进去
}6、求二叉树叶子个数
把二叉树中没有孩子结点的结点称为叶子结点。
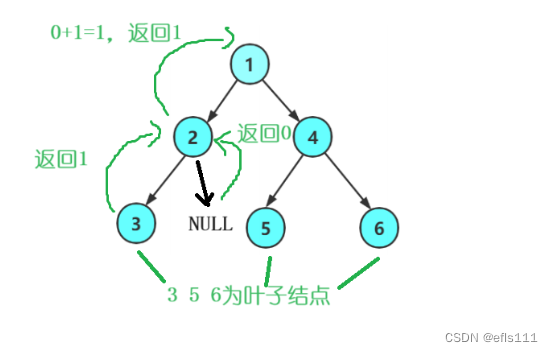
因此叶子节点的特性是其他节点不具有的,既:左孩子和右孩子都为空。因此当递归至某个结点的时候发现其左孩子和右孩子都为空,则计数+1。
求二叉树叶子个数代码如下:
int BinaryTreeLeafSize(TNode* root)//叶子个数
{
if (root == NULL)//为空则不是叶子结点
return 0;
if (root->left == NULL && root->right == NULL)//左右孩子都为空则返回1
{
return 1;
}
else
return BinaryTreeLeafSize(root->left)//递归左子树
+ BinaryTreeLeafSize(root->right);//递归右子树
}7、求第k层结点总数
比如求该二叉树的第三层结点总数。思路:从上往下看,如果求第三层,可以转换成求结点1的第三层,求结点2和4的第二层,求结点3 5 6 的第一层,都表示为该树的第三层,只是表达不一样。因此当k==1的时候说明这时候是在第k层。

求第k层结点总数代码如下:
int BinaryTreeLevelKSize(TNode* root, int k)//求第k层结点的总数
{
if (root == NULL)
return 0;
if (k == 1)
return 1;
//递归函数,k不断-1
return BinaryTreeLevelKSize(root->left, k - 1)//递归左子树
+ BinaryTreeLevelKSize(root->right, k - 1);//递归右子树
}8、求二叉树的高度
思路:先遍历到最底层,然后收回的时候每一层+1,取左子树递归函数的值与右子树递归函数的值的较大值加上该层高度1就是该层的高度。示意图如下:
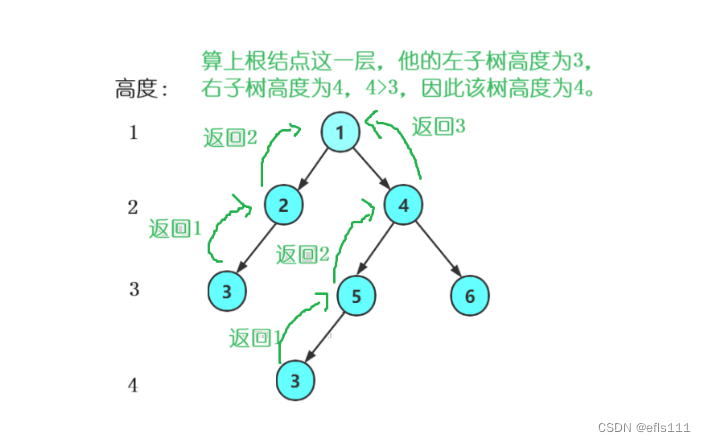
二叉树的高度代码如下:
int BinaryTreeHeight(TNode* root)//二叉树高度
{
if (root == NULL)
return 0;
//递归函数
int leftHeight = BinaryTreeHeight(root->left);//将左子树的高度存在一个变量中
int rightHeight = BinaryTreeHeight(root->right);//将右子树的高度存在一个变量中
//取两个变量的较大者加上该层的高度1
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}9、从二叉树中查找值为x的结点
思路:若找到该节点,则返回该节点的地址,并且用一个指针变量来接收,之后的代码就不需要再运行。
二叉树查找代码如下:
TNode* BinaryTreeFind(TNode* root, TreeDataType x)//查找值为x的结点
{
if (root == NULL)//为空返回NULL
return NULL;
if (root->data == x)//若找到了则返回该结点的地址
return root;
TNode* xpoi= BinaryTreeFind(root->left, x);//递归左子树,找到了就存放在指针变量xpoi中
if (xpoi != NULL)//如果没有找到就不执行if语句,则继续找
return xpoi;
xpoi= BinaryTreeFind(root->right,x);//递归右子树
if (xpoi != NULL)
return xpoi;
return NULL;//若都没有找到则返回NULL给上层函数
}10、层序遍历
层序遍历的逻辑与前、中、后遍历的逻辑不一样,前、中、后遍历用的是递归的逻辑,而层序遍历则是采用非递归的逻辑。

层序遍历的顺序如上图:1 2 4 3 5 6,他的思路是把树节点放入队列中,队列的逻辑是先进先出、后进后出, 因此先把根节点1放入队列中,然后出队的时候是先出的1,同时把1的两个孩子入队,此时队列中存放的是2 4,并且下一次出队先将2出掉,同时把2的孩子入队,此时队列里存放的是4 1,如此下去,最后出队的顺序为1 2 4 3 5 6,与层序遍历的顺序一样。
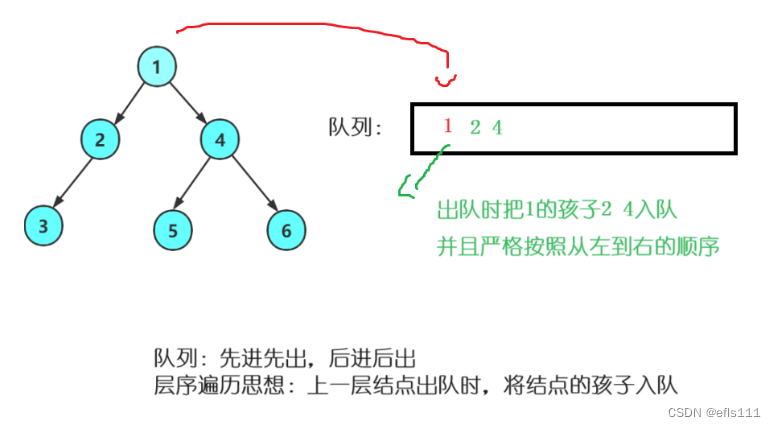
因此层序遍历的代码涉及队列的创建:
//队列结构体
typedef struct TreeNode* QueueDataType;
typedef struct QNode
{
struct QNode* next;
QueueDataType data;
}QNode;
typedef struct Queue
{
struct QNode* head;
struct QNode* tail;
int size;
}Queue;
void QueueInit(Queue* pq)//队列初始化
{
assert(pq);
pq->head = NULL;
pq->tail = NULL;
pq->size = 0;
}
void QueuePush(Queue* pq, QueueDataType x)//入队
{
assert(pq);
QNode* newnode = BuyNode(x);
if (pq->head == NULL)
{
assert(pq->tail==NULL);
pq->head = pq->tail = newnode;
}
else
{
pq->tail->next = newnode;
pq->tail = newnode;
}
pq->size++;
}
bool Empty(Queue* pq)//判空
{
assert(pq);
return pq->head == NULL
|| pq->tail==NULL;
}
QueueDataType QueueFront(Queue* pq)//显示队头数据
{
assert(pq);
assert(!Empty(pq));
return pq->head->data;
}
void QueuePop(Queue* pq)//出队
{
assert(pq);
assert(!Empty(pq));
if (pq->head == pq->tail)//一个节点
{
free(pq->head);
pq->head = pq->tail = NULL;
}
else//多个节点
{
QNode* poi = pq->head;
pq->head = pq->head->next;
free(poi);
}
pq->size--;
}
void QueueDestroy(Queue* pq)//释放队列
{
assert(pq);
QNode* cur = pq->head;
while (cur)
{
QNode* poi = cur->next;
free(cur);
cur = poi;
}
pq->head = pq->tail = NULL;
pq->size = 0;
}
//层序遍历
void LevelOrder(TNode* root)
{
Queue q;
QueueInit(&q);
if(root!=NULL)
QueuePush(&q, root);
while (!Empty(&q))
{
TNode* front=QueueFront(&q);
QueuePop(&q);
printf("%d ", front->data);
if(front->left)
QueuePush(&q, front->left);
if(front->right)
QueuePush(&q, front->right);
}
QueueDestroy(&q);
}11、二叉树的销毁
由于二叉树是在堆上申请而来的,因此再使用完之后要对申请的空间进行释放。这里选择用后序的方法进行释放,原因是后序的顺序是:左子树-右子树-根,根是最后才释放的,如果用前序遍历释放就会出现先把根释放了,就不好找根的左子树和右子树了,中序遍历也同理。
二叉树销毁代码如下:
void BinaryTreeDestory(TNode* root)//二叉树销毁
{
if (root == NULL)
return;
//后序遍历
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
free(root);
}12、测试功能
上述解析了如此多的功能,接下来对其进行测试,观察运行结果。
测试代码如下:
int main()
{
TNode* root = CreatTree();//创建树,并返回根结点
PreOrder(root);//前序遍历
printf("\ntreesize:%d", BinaryTreeSize(root));//树的结点个数
printf("\ntreesize:%d", BinaryTreeSize(root));
printf("\nLeafSize:%d", BinaryTreeLeafSize(root));//叶子个数
printf("\nLevelKSize:%d", BinaryTreeLevelKSize(root, 3));//第k层结点个数
printf("\nheight:%d", BinaryTreeHeight(root));//树的高度
TNode* xpoi = BinaryTreeFind(root, 3);//查找结点
if (xpoi == NULL)
printf("二叉树无该结点\n");
else
printf("\n找到结点:%d", xpoi->data);
printf("\n");
LevelOrder(root);//层序遍历
BinaryTreeDestory(root);//二叉树释放
root = NULL;//手动置空
return 0;
}运行结果:

从运行结果来看,以上功能均可正常运行。
结语:
以上就是关于二叉树以及相关功能的实现与解析,二叉树的重点在于对函数递归的形象理解,本质上二叉树就是运用函数不断递归实现的,看似一小段代码实则可以延长出很多信息。最后希望本文可以给你带来更多的收获,如果本文对你起到了帮助,希望可以动动小指头帮忙点赞👍+关注😎+收藏👌!如果有遗漏或者有误的地方欢迎大家在评论区补充~!!谢谢大家!!
(~ ̄▽ ̄)~