目录
一、高精度概念
二、高精度算法的实现
1、高精度加法(大整数相加)
2、高精度减法(大整数减法)
3、高精度乘法(大整数*小整数)
4、高精度除法(大整数/小整数)
一、高精度概念
高精度算法,是一种处理大数字的数学计算方法。在一般的科学计算中,会经常算到小数点后几百位或者更多,当然也可能是几百亿的大数字。一般这类数字统称为高精度数,高精度算法是用计算机对于超大数据的一种模拟加,减,乘,除,乘方,阶乘等运算。对于非常庞大的数字无法在计算机中正常存储。于是,将这个数字拆开成一位一位的,或者是四位四位的存储到一个数组中, 用一个数组去表示一个数字,这样这个数字就被称为是高精度数。
高精度就是说参与运算的数据和运算结果的范围,超出标准数据类型能表示的数据大小范围的运算。此时如果要得到正确的计算结果,就不能依靠普通方法实现了,而要在普通运算原理的基础上,加以辅助算法来实现超大数据的计算。
例如:求两个 500 位的数据相乘的结果,这时就要用到高精度算法了。
二、高精度算法的实现
1、高精度加法(大整数相加)
大整数又称为高精度整数,其含义就是用基本数据类型无法存储其精度的整数。 大整数的存储使用数组即可。

思路:
先将大整数倒序存储,然后从左往右相加,这样才算是从低位往高位加,并判断是否有进位,加出来的数取余后尾插到要保存的vector中,这样求出来的数还是逆序的,但是主函数会从后往前读。
AC代码:
#include<iostream>
#include<string>
#include<vector>
using namespace std;
//1、高精度加法(大整数加法)
vector<int> add(vector<int>& A, vector<int>& B)
{
//如果B更大,因为下面代码都是以第一个形参作为for结束条件,所以要让大的是第一个形参
if (A.size() < B.size()) return add(B, A);
vector<int> C;
int t = 0; //用来判断是否进位
//注意这里是逆序的数从前往后加的
for (int i = 0; i < A.size(); ++i)
{//for循环是以大的数来作为循环结束条件的
t += A[i];//for循环以A为结束条件,这里不用格外判断
if (i < B.size()) t += B[i];//因没以B为结束条件,故这里要格外判断是否可以加
C.push_back(t % 10);//加出来的数要的是余数
t /= 10; //判断是否有进位
}
if (t) C.push_back(t);//有可能最后加完还有进位
//第二种写法
//这种写法不用格外判断最后是否有进位
//for (int i = 0, t = 0; i < A.size()||t; ++i)
//{
// if (i < A.size()) t += A[i];//因为有t作为条件,故这里要格外判断
// if (i < B.size()) t += B[i];//因没以B为结束条件,故这里要格外判断是否可以加
// C.push_back(t % 10);//加出来的数要的是余数
// t /= 10; //判断是否有进位
//}
return C;
}
int main()
{
string a, b;
cin >> a >> b;
vector<int> A, B;
//把字符串逆序存入vector中,方便后续计算
for (int i = a.size() - 1; i >= 0; --i) A.push_back(a[i] - '0');
for (int i = b.size() - 1; i >= 0; --i) B.push_back(b[i] - '0');
auto C = add(A, B);
for (int i = C.size() - 1; i >= 0; --i) cout << C[i];
cout << endl;
return 0;
}2、高精度减法(大整数减法)
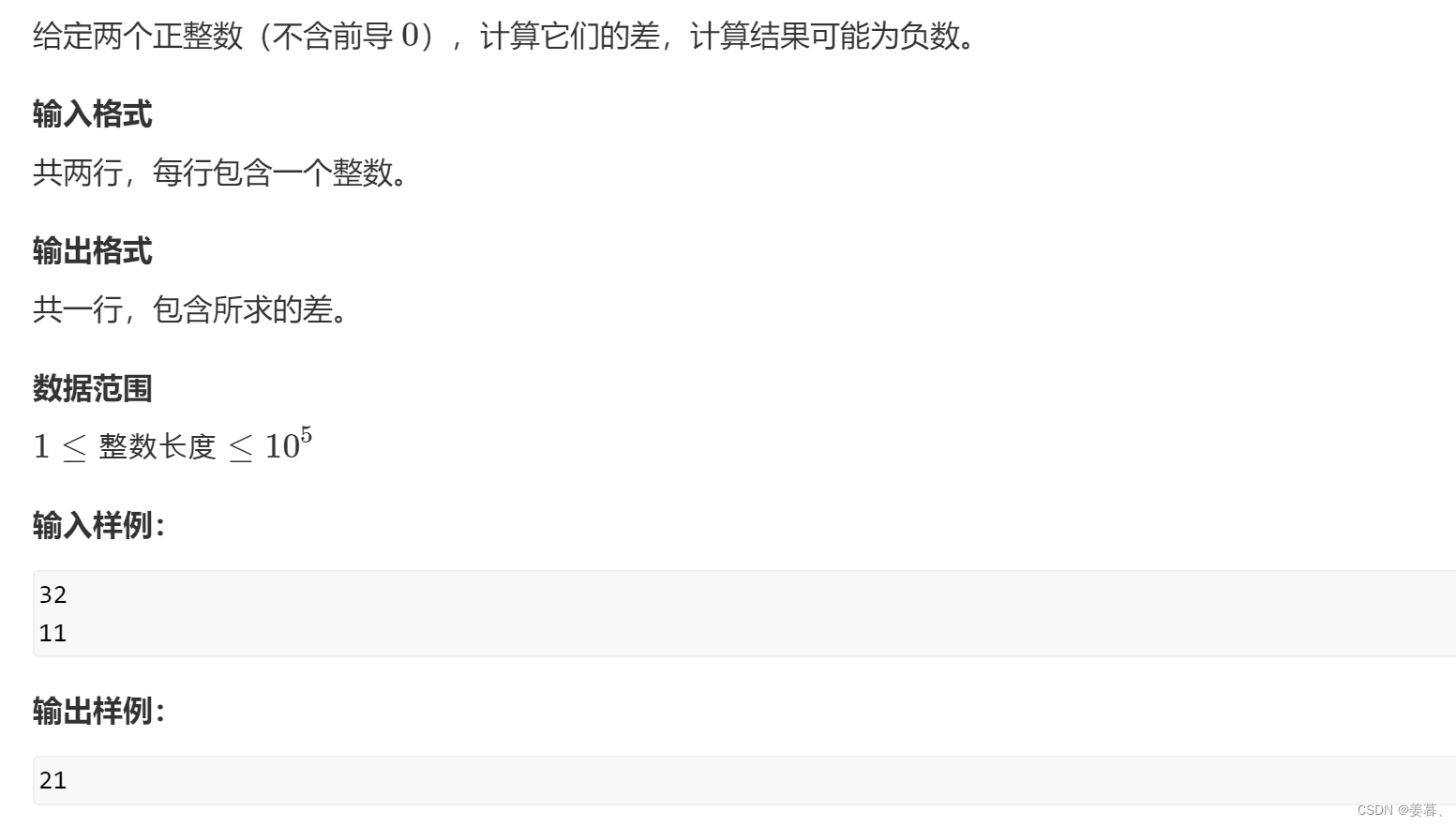
思路:
和加法区别在于其一,减法是要借位而不是进位,其二,减法会导致有前导0存在。
什么是前导0?比如124-113,我们存的是421,311,相减时是4-3=1,2-1=1,1-1=0,然后尾插导致C为110,我们最后是逆着读的,即011,(但正常124-113=11),这里011肯定不对,多了一个前导0,故我们最后要把这个前导0去掉变成11,然后逆着读出来就对了
AC代码:
#include<iostream>
#include<string>
#include<vector>
using namespace std;
//比较哪个数大,注意这里的数是从倒序存的,故后面的才是高位
bool cmp(vector<int>& A, vector<int>& B)
{
if (A.size() != B.size()) return A.size() > B.size();
for (int i = A.size() - 1; i >= 0; --i)
if (A[i] != B[i])
return A[i] > B[i];//不等从高位开始比
return true;//相等
}
vector<int> sub(vector<int>& A, vector<int>& B)
{//利用cmp函数比较,使大的数一定是A,与for循环代码相符
vector<int> C;
int t = 0;//判断借位
for (int i = 0; i < A.size(); ++i)
{
t = A[i] - t;//每次都会减掉借位
if (i < B.size()) t -= B[i];
//关于(t+10)%10(t是减出来的数)
//t若为正数(但<=9)其=t%10+10%10=t
//t若为负数,正好可以借位+10然后取余数即可
C.push_back((t + 10) % 10);
if (t >= 0) t = 0;
else t = 1; //<0肯定有借位了
}
//因为两个数相减会导致有多余的0出现,故去除前导0
//size()>1是因为可能真的相减出现0,这种0不算前导0
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a, b;
cin >> a >> b;
vector<int> A, B;
//把字符串逆序存入vector中,方便后续计算
for (int i = a.size() - 1; i >= 0; --i) A.push_back(a[i] - '0');
for (int i = b.size() - 1; i >= 0; --i) B.push_back(b[i] - '0');
vector<int> C;
if (cmp(A, B)) C = sub(A, B); //正数
else cout << "-", C = sub(B, A); //负数
for (int i = C.size() - 1; i >= 0; --i) cout << C[i];
cout << endl;
return 0;
}
3、高精度乘法(大整数*小整数)

思路:

AC代码:
#include<iostream>
#include<string>
#include<vector>
using namespace std;
vector<int> mul(vector<int>& A, int b)
{
vector<int> C;
for (int i = 0, t = 0; i < A.size() || t; ++i)
{
if (i < A.size()) t += A[i] * b;//加上t是因为上一次可能有乘出来的进位
C.push_back(t % 10);
t /= 10;//计算进位
}
//当b是0时,会出现前导0
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector<int> A;
for (int i = a.size() - 1; i >= 0; --i) A.push_back(a[i] - '0');
auto C = mul(A, b);
for (int i = C.size() - 1; i >= 0; --i) cout << C[i];
cout << endl;
return 0;
}4、高精度除法(大整数/小整数)

思路:

AC代码:
#include<iostream>
#include<string>
#include<vector>
#include<algorithm>
using namespace std;
vector<int> div(vector<int>& A, int b, int& r)
{
vector<int> C;
for (int i = A.size() - 1; i >= 0; --i)
{
r = r * 10 + A[i];
C.push_back(r / b);
r %= b; //计算余数
}
//逆置:因为我们是正常求,但最后是倒着读的,且便于去除前导0
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector<int> A;
for (int i = a.size() - 1; i >= 0; --i) A.push_back(a[i] - '0');
int r = 0; //余数
auto C = div(A, b, r);
for (int i = C.size() - 1; i >= 0; --i) cout << C[i];
cout << endl << r << endl;
return 0;
}