目录
- 前言
- 二叉查找树(Binary Search Tree)
- 二叉查找树的时间复杂度分析
- 解答开篇
- 内容小结
前言

本节课程思维导图:
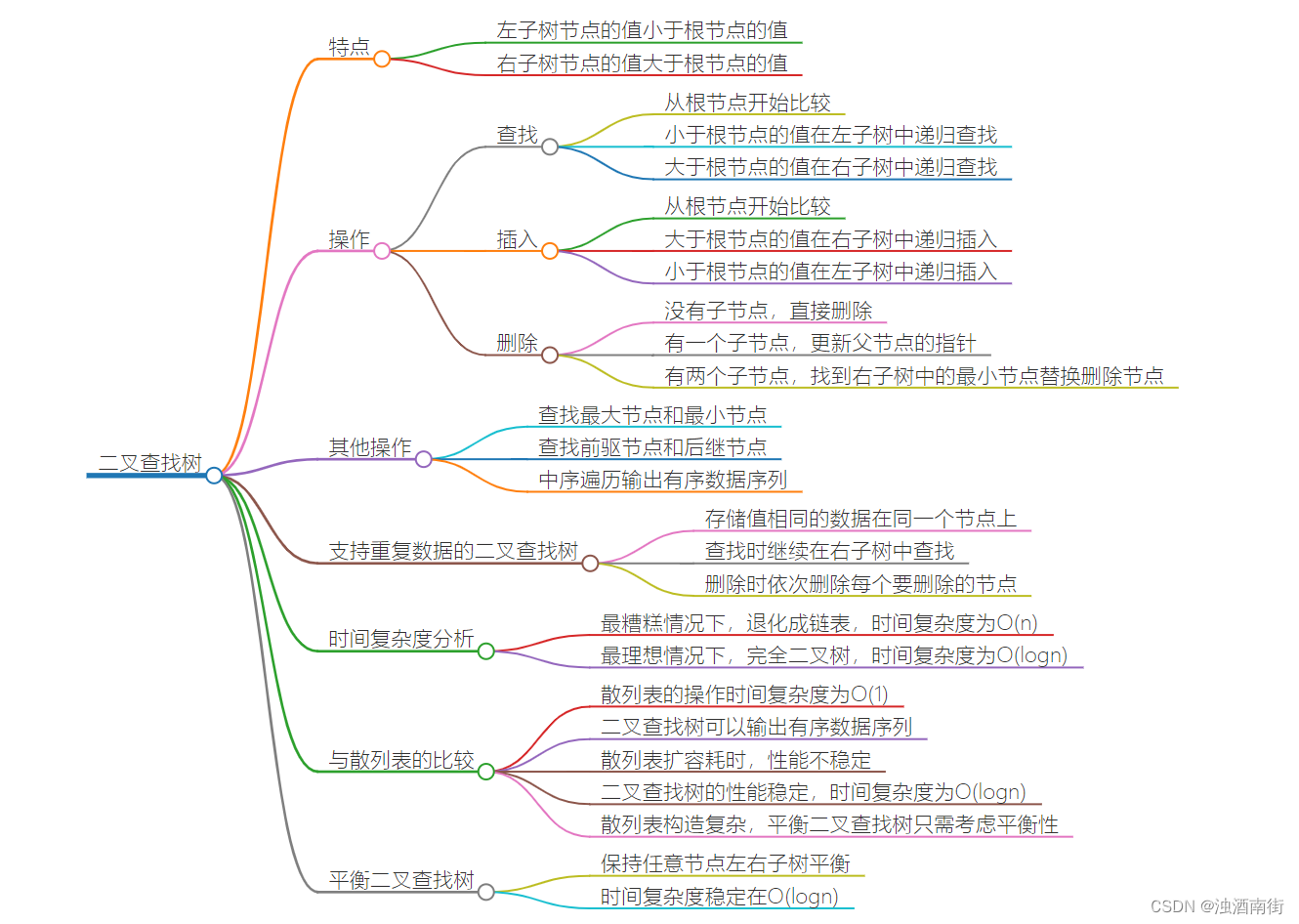
二叉查找树最大的特点就是,支持动态数据集合的快速插入、删除、查找操作。我们之前说过,散列表也是支持这些操作的,并且散列表的这些操作比二叉查找树更高效,时间复杂度是 O(1)。既然有了这么高效的散列表,使用二叉树的地方是不是都可以替换成散列表呢?有没有哪些地方是散列表做不了,必须要用二叉树来做的呢?
二叉查找树(Binary Search Tree)
二叉查找树是二叉树中最常用的一种类型,也叫二叉搜索树。顾名思义,二叉查找树是为了实现快速查找而生的。不过,它不仅仅支持快速查找一个数据,还支持快速插入、删除一个数据。
二叉查找树要求,在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值。
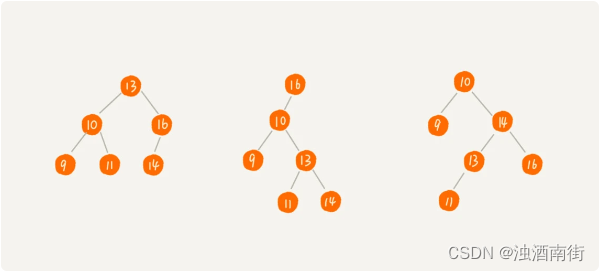
二叉查找树支持快速查找、插入、删除操作,现在我们就依次来看下,这三个操作是如何实现的。
- 二叉查找树的查找操作
首先,我们看如何在二叉查找树中查找一个节点。我们先取根节点,如果它等于我们要查找的数据,那就返回。如果要查找的数据比根节点的值小,那就在左子树中递归查找;如果要查找的数据比根节点的值大,那就在右子树中递归查找。
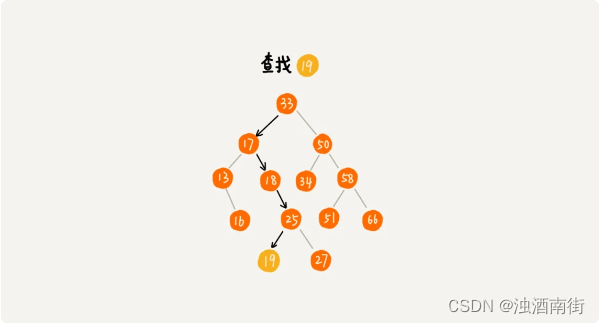
代码:
public class BinarySearchTree {
private Node tree;
public Node find(int data) {
Node p = tree;
while (p != null) {
if (data < p.data) p = p.left;
else if (data > p.data) p = p.right;
else return p;
}
return null;
}
public static class Node {
private int data;
private Node left;
private Node right;
public Node(int data) {
this.data = data;
}
}
}
- 二叉查找树的插入操作
二叉查找树的插入过程有点类似查找操作。新插入的数据一般都是在叶子节点上,所以我们只需要从根节点开始,依次比较要插入的数据和节点的大小关系。如果要插入的数据比节点的数据大,并且节点的右子树为空,就将新数据直接插到右子节点的位置;如果不为空,就再递归遍历右子树,查找插入位置。同理,如果要插入的数据比节点数值小,并且节点的左子树为空,就将新数据插入到左子节点的位置;如果不为空,就再递归遍历左子树,查找插入位置。
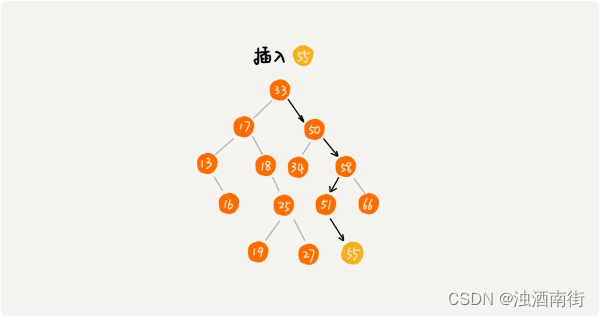
代码:
public void insert(int data) {
if (tree == null) {
tree = new Node(data);
return;
}
Node p = tree;
while (p != null) {
if (data > p.data) {
if (p.right == null) {
p.right = new Node(data);
return;
}
p = p.right;
} else { // data < p.data
if (p.left == null) {
p.left = new Node(data);
return;
}
p = p.left;
}
}
}
- 二叉查找树的删除操作
针对要删除节点的子节点个数的不同,我们需要分三种情况来处理。
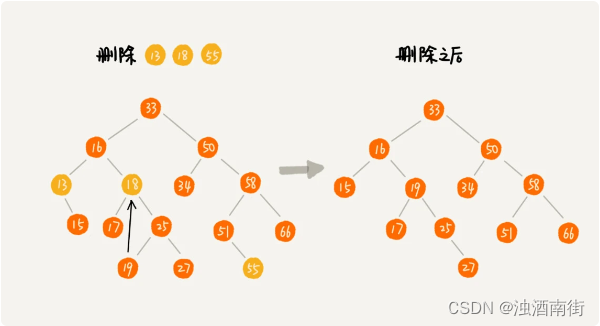
第一种情况是,如果要删除的节点没有子节点,我们只需要直接将父节点中,指向要删除节点的指针置为 null。比如图中的删除节点 55。
第二种情况是,如果要删除的节点只有一个子节点(只有左子节点或者右子节点),我们只需要更新父节点中,指向要删除节点的指针,让它指向要删除节点的子节点就可以了。比如图中的删除节点 13。
第三种情况是,如果要删除的节点有两个子节点,这就比较复杂了。我们需要找到这个节点的右子树中的最小节点,把它替换到要删除的节点上。然后再删除掉这个最小节点,因为最小节点肯定没有左子节点(如果有左子结点,那就不是最小节点了),所以,我们可以应用上面两条规则来删除这个最小节点。比如图中的删除节点 18。
- 二叉查找树的其他操作
除了插入、删除、查找操作之外,二叉查找树中还可以支持快速地查找最大节点和最小节点、前驱节点和后继节点。
还有一个重要的特性,就是中序遍历二叉查找树,可以输出有序的数据序列,时间复杂度是 O(n),非常高效。因此,二叉查找树也叫作二叉排序树。
二叉查找树的时间复杂度分析
我们来分析一下,二叉查找树的插入、删除、查找操作的时间复杂度。
实际上,二叉查找树的形态各式各样。它们的查找、插入、删除操作的执行效率都是不一样的。下图二叉查找树,根节点的左右子树极度不平衡,已经退化成了链表,所以查找的时间复杂度就变成了 O(n)。
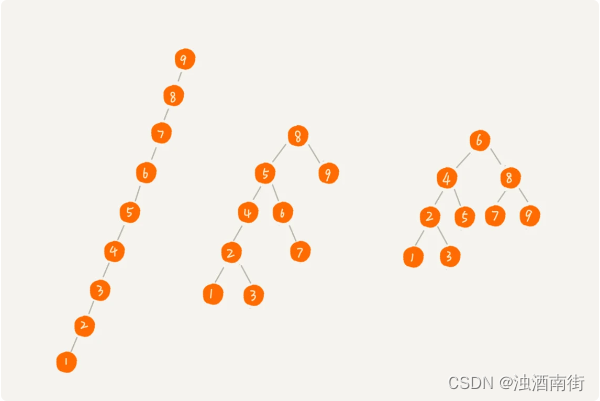
我们现在来分析一个最理想的情况,二叉查找树是一棵完全二叉树(或满二叉树)。这个时候,插入、删除、查找的时间复杂度是多少呢?
不管操作是插入、删除还是查找,时间复杂度其实都跟树的高度成正比,也就是 O(height)。既然这样,现在问题就转变成另外一个了,也就是,如何求一棵包含 n 个节点的完全二叉树的高度?
树的高度就等于最大层数减一,为了方便计算,我们转换成层来表示。从图中可以看出,包含 n 个节点的完全二叉树中,第一层包含 1 个节点,第二层包含 2 个节点,第三层包含 4 个节点,依次类推,下面一层节点个数是上一层的 2 倍,第 K 层包含的节点个数就是 2^(K-1)。不过,对于完全二叉树来说,最后一层的节点个数有点儿不遵守上面的规律了。它包含的节点个数在 1 个到 2^(L-1) 个之间(我们假设最大层数是 L)。如果我们把每一层的节点个数加起来就是总的节点个数 n。也就是说,如果节点的个数是 n,那么 n 满足这样一个关系:
n >= 1+2+4+8+...+2^(L-2)+1
n <= 1+2+4+8+...+2^(L-2)+2^(L-1)
借助等比数列的求和公式,我们可以计算出,L 的范围是[log2(n+1), log2n +1]。完全二叉树的层数小于等于 log2n +1,也就是说,完全二叉树的高度小于等于 log2n。
显然,极度不平衡的二叉查找树,它的查找性能肯定不能满足我们的需求。我们需要构建一种不管怎么删除、插入数据,在任何时候,都能保持任意节点左右子树都比较平衡的二叉查找树,一种特殊的二叉查找树,平衡二叉查找树。平衡二叉查找树的高度接近 logn,所以插入、删除、查找操作的时间复杂度也比较稳定,是 O(logn)。
解答开篇
散列表的插入、删除、查找操作的时间复杂度可以做到常量级的 O(1),非常高效。而二叉查找树在比较平衡的情况下,插入、删除、查找操作时间复杂度才是 O(logn),相对散列表,好像并没有什么优势,那我们为什么还要用二叉查找树呢?
我认为有下面几个原因:
第一,散列表中的数据是无序存储的,如果要输出有序的数据,需要先进行排序。而对于二叉查找树来说,我们只需要中序遍历,就可以在 O(n) 的时间复杂度内,输出有序的数据序列。
第二,散列表扩容耗时很多,而且当遇到散列冲突时,性能不稳定,尽管二叉查找树的性能不稳定,但是在工程中,我们最常用的平衡二叉查找树的性能非常稳定,时间复杂度稳定在 O(logn)。
第三,笼统地来说,尽管散列表的查找等操作的时间复杂度是常量级的,但因为哈希冲突的存在,这个常量不一定比 logn 小,所以实际的查找速度可能不一定比 O(logn) 快。加上哈希函数的耗时,也不一定就比平衡二叉查找树的效率高。
第四,散列表的构造比二叉查找树要复杂,需要考虑的东西很多。比如散列函数的设计、冲突解决办法、扩容、缩容等。平衡二叉查找树只需要考虑平衡性这一个问题,而且这个问题的解决方案比较成熟、固定。
最后,为了避免过多的散列冲突,散列表装载因子不能太大,特别是基于开放寻址法解决冲突的散列表,不然会浪费一定的存储空间。综合这几点,平衡二叉查找树在某些方面还是优于散列表的,所以,这两者的存在并不冲突。我们在实际的开发过程中,需要结合具体的需求来选择使用哪一个。
内容小结
二叉查找树。它支持快速地查找、插入、删除操作。二叉查找树中,每个节点的值都大于左子树节点的值,小于右子树节点的值。
在二叉查找树中,查找、插入、删除等很多操作的时间复杂度都跟树的高度成正比。两个极端情况的时间复杂度分别是 O(n) 和 O(logn),分别对应二叉树退化成链表的情况和完全二叉树。为了避免时间复杂度的退化,针对二叉查找树,我们又设计了一种更加复杂的树,平衡二叉查找树,时间复杂度可以做到稳定的 O(logn)。