06 matlab中NSCT的使用

最近在学习NSCT相关内容，奈何网上资源太少，简单看了些论文找了一些帖子才懂了一点点，在此分享给大家，希望有所帮助。

一.NSCT流程

首先我们先梳理一下NSCT变换的流程，只有清楚流程才更好的理清NSCT工具箱里的代码，才能够根据自己的需要进行灵活使用。

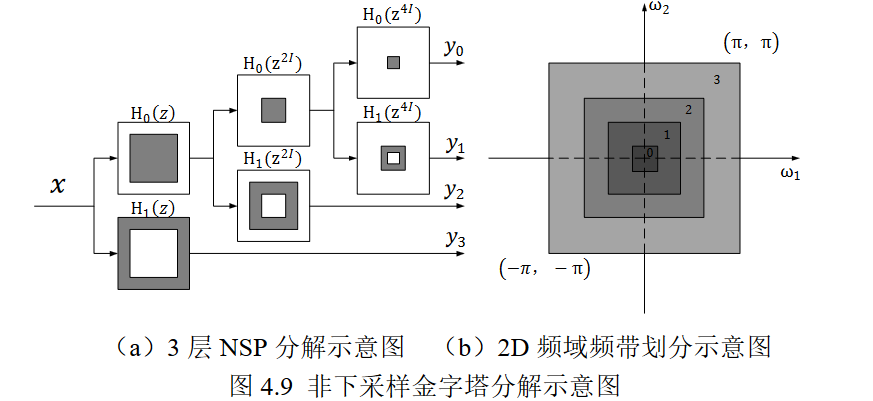
①NSPFB进行非下采样金子塔分解将图像分解为低频和高频分量，比如下图所示，进行三层分解就可以得到三个高频分量和一个低频分量。

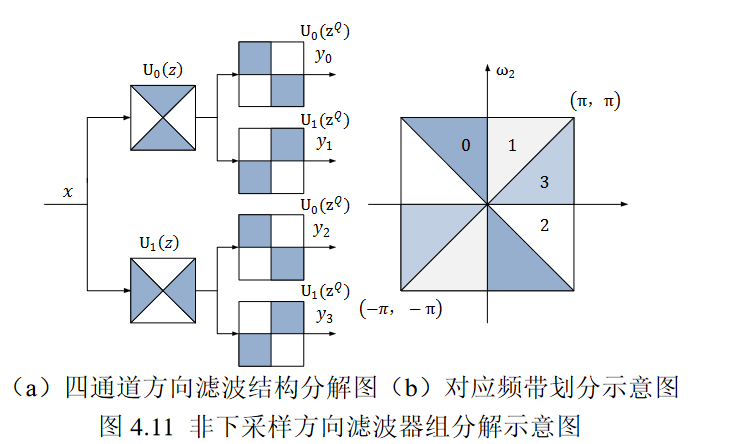
②NSDFB对NSP分解后的高频分量进行方向分解，在不同方向上进行分解，分解成为不同方向上的细节信息。

③经过上面两个步骤，我们其实就已经实现了NSCT分解的全部过程，如下图所示。

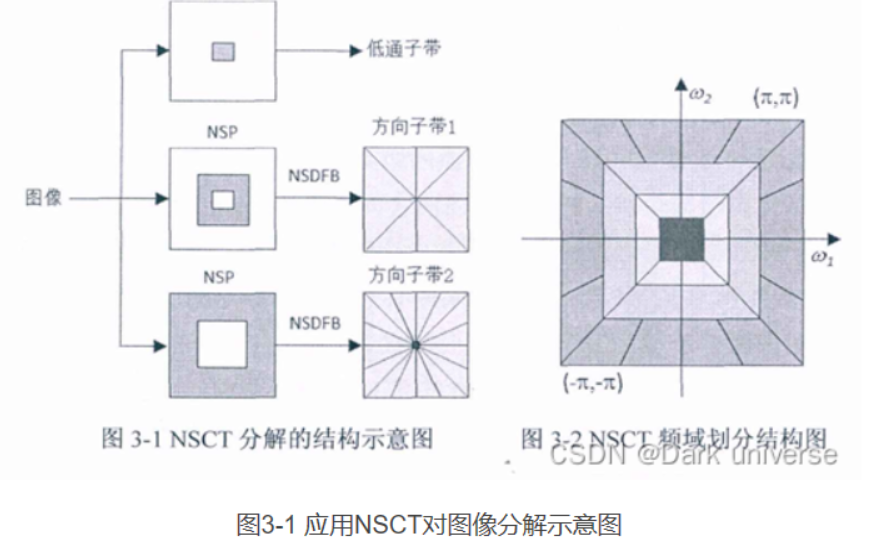
④那么如何进行图像的重构呢，这是针对我目前应用到的图像融合进行分析的，我们利用制定好的图像融合的规则，分别将低频分量，和各个方向上的信息进行融合，最终得到的是将两个上图所示的结构又变成了一个这样结构。

⑤将各个方向的频率信息合在一起得到每一层总的高频信息，3-1的结构又变回了金字塔结构，之后我们只要进行金字塔重构即可，从底层到顶层这样一个过程。
至此虽然忽略掉了一些细节（虽然我也不太懂），我们大概理清了NSCT分解和图像重构的这样一个流程，搞懂这个流程再去看代码自然就事半功倍了。

二. matlab关键代码解析

1.小试牛刀（搞懂一个函数快速上手使用）

关键函数：NSCT再matlab NSCT 工具箱中仅仅下面一个函数即可实现。

y = nsctdec(x, levels, [dfilt, pfilt] )

• x:图像的输入矩阵，双精度数据类型
• levels:方向滤波器组分解层数向量,注意是一组向量值，比如[1 2 3],就是说明对第一层高频分量进行2个方向分解，第二层4方向分解，第三层8方向分解。
• dfilt:方向滤波器组
• pfilt:塔式分解的滤波器组
• out:输出的结果是一组向量集合，集合第一个向量是低频分量的二维数组，接下来是从小到大排列高频子带。

经过三次分解后，我们输出一下每层的信息（注意inshow中我引用的格式，关注一些cell里面输出内容，就可以上手使用了）

subplot(2,2,2);
imshow(Insp{1,1},[]);
 title('低频分量');
subplot(2,2,3);
imshow(Insp{1,2}{1,1},[]);
 title('高频1');
subplot(2,2,4);
imshow(Insp{1,2}{1,2},[]);
 title('高频1');

2.登堂入室（看看这个函数背后的细节）

这个函数所实现的无外乎就是在上文中所讲诉的流程，想了想没必要仔细去讲，下面是完整注释版代码，大家对着注释好好看一下就好。

function [Insp,Insct]= myNSCTd(I,levels,pfiltername,dfiltername,type)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%函数功能：完成图像的level级NSCT分解
%%函数输入：I	——输入源图像
%          levels	——分解级别的数组，例如[1,2,3],分解的方向数分别为[2,4,8].
%          pfiltername	——塔式分解滤波器名称
%          dfiltername  ——方向分解滤波器名称
%%函数输出：Insct    ——输出为cell类型，包括低通以及各级别各方向的分量
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%                      
 
%%%%%%%%生成非下采样金字塔滤波器组%%%%%%%%%%%%%
%该函数为copy的，可选参数如下：
%'9-7'、'maxflat'、'pyr'、'pyrexc'
%输出的h0，h1是金字塔分解滤波器
%输出的g0，g1是金字塔重构滤波器
[ph0, ph1, pg0, pg1] = atrousfilters(pfiltername);%无法改进
 
%%%%%%%%%生成非下采样方向滤波器组%%%%%%%%%%%%%
%建立一个4*4的空矩阵，存放滤波器组
filtersd = cell(4) ;
 
%function [h0, h1] = dfilters(fname, type)
%copy的函数，作用是根据名字生成方向滤波器
%fname的可选参数有：'haar'、'vk'、'ko'、'kos'、
%'lax'、'sk'、'cd'、'pkva'、'oqf_362'、'sinc'
%其中测验结果看的比较舒服的有'lax'、'sk'、'cd'
%最理想的是'pkva'，copy函数中的ldfilter.m、
%ld2quin.m和qupz.m都是用语生成该滤波器
%type的可选参数有：'d'、'r'，分别表示生成分解
%滤波器和重构滤波器。
%输出的h0为小波函数(高频)，h1为尺度函数(低频)
[dh1, dh2] = dfilters(dfiltername, 'd'); %无法改进
dh1 = dh1./sqrt(2) ;
dh2 = dh2./sqrt(2) ;
 
%function y = modulate2(f, type, center)
%copy的函数，作用是将输入的方向滤波器f依据type类型增加方向性
%type可选参数有：'r'生成横向梳状滤波器、'c'生成纵向梳状滤%波器、
%'d'生成网格型滤波器(综合横纵梳状滤波器的特点)
%center参数，对输入滤波器的初始中心作确定，通常默认为[0 0]。
filtersd{1} = modulate2(dh1, 'c');%无法改进
filtersd{2} = modulate2(dh2, 'c');%无法改进
 
%function [y1, y2] = parafilters( f1, f2 )
%copy的函数，输入是两个滤波器，输出是两个滤波器组
%作用是将输入的两个滤波器分别增加行列方向性之后
%再分别转置，生成四个不同的滤波器
%随后循环调用function y = resampz(x, type, shift)
%copy的函数，输入是单个滤波器x，type是上面生成的四个滤波器
%中的第几个，shift通常不输入，为默认值1.
%对每个滤波器作旋转，即生成四个旋转后的方向滤波器。
%综合结果：
%对输入的两个滤波器，输出两组旋转后的滤波器，每组四个
[filtersd{3}, filtersd{4}] = parafilters( dh1, dh2 ) ;%无法改进
 
%判断分解层数
clevels = length( levels );
%初始化输出缓存
nIndex = clevels + 1 ;
y = cell(1, nIndex) ;
Insp=cell(1,clevels);
 
%NSCT分解
for i= 1 : clevels   
 
    %对图像进行金字塔分解，xlo为低通输出，xhi为高通输出
    switch type
        case 'NSCT'
            [Ilow, Ihigh] = NSPd(I, ph0, ph1, i-1) ;%无法改进
            %NSPlow{i}=Ihigh;
        case 'NewPM'
            [Ilow,Ihigh]=Newmcd(I);
    end
  
    %如果方向分解级别不为0，进行方向分解，并将结果存入y的对应部分
    if levels(nIndex-1) > 0 
        % function nsdfbdec中，在level高于3的时候，采样矩阵M的设定不懂，
        % 所以只能copy过来。
      
        Ihigh_dir = nsdfbdec(Ihigh, filtersd, levels(nIndex-1));      
        y{nIndex}=Ihigh_dir ;
      
 
    %若方向分解级别为0，直接复制
    else 
        y{nIndex}=xhigh ;
    end
  
    %更新输出缓存指针
    nIndex = nIndex - 1 ;
  
    %更新图像为分解的低通部分，进行下一次迭代
    I = Ilow ;
    Insp{i}=I;
end
 
% 输出的第一副图为最后的低通结果。
y{1}=I;
Insct=y;
 
end

‍