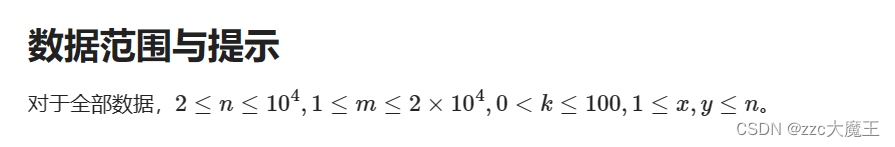
---

分析

根据数据范围分析一下复杂度，Floyd和dj算法都必爆。

发现题目说的是树，还是边还是双向的（树本身就是无向的，连通无回路的无向图叫做无向树，简称树。如果题目说了树，那么默认边就是双向的），也没指明根节点，那么就是无根树，任选一个节点当根节点。

思路

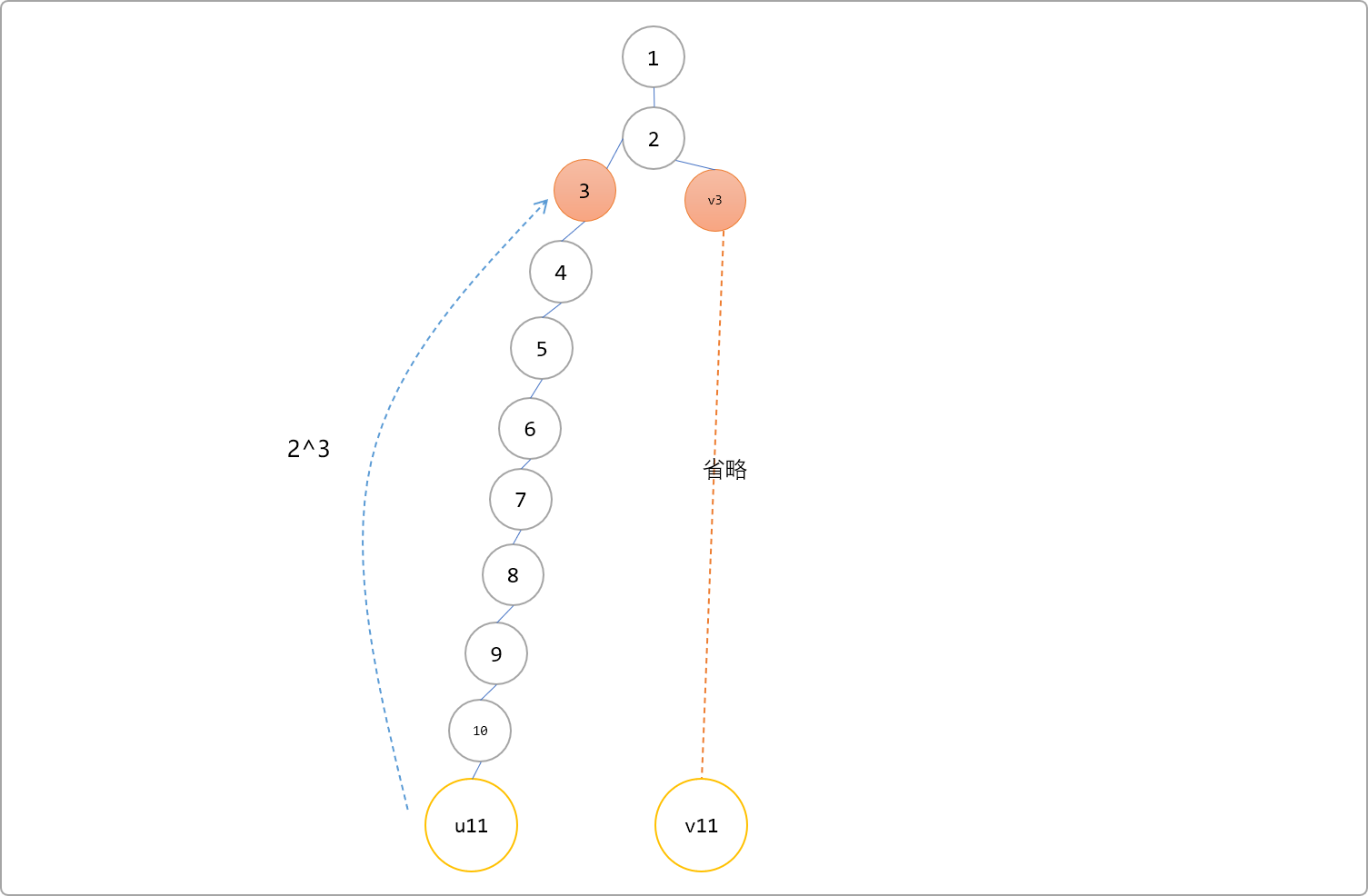
是树的话就简单了，任意两点之间的最短距离很容易想到最近公共祖先，x到LCA的距离加上y到LCA的距离就是最短距离。

考虑在LCA预处理的dfs里面加上dis数组维护每个节点到根节点的距离。

那么x，y两点的最短距离就是dis[x]+dis[y]-2*dis[lca(x,y)]

AC代码

#include <bits/stdc++.h>
using namespace std;

inline int read(){
    int x=0;char c=getchar();
    while(c<48 or c>57)c=getchar();
    while(c>=48 and c<=57)x=(x<<3)+(x<<1)+(c xor 48),c=getchar();
    return x;
}

using pii=pair<int,int>;
const int N=1e4+5;
int n,m,lg[N],d[N],f[N][15],dis[N];
vector<pii>e[N];
bitset<N>vis;

void dfs(int now,int fa){
    if(vis[now])return;//使用vector别忘了加vis，不然会访问父节点
    vis[now]=true;
    f[now][0]=fa;
    d[now]=d[fa]+1;
    for(int i=1;i<=lg[d[now]];++i)
        f[now][i]=f[f[now][i-1]][i-1];
    for(auto i:e[now]){
        if(!vis[i.second]){
            dis[i.second]=dis[now]+i.first;
            dfs(i.second,now);
        }
    }
}
int lca(int x,int y){
    if(d[x]<d[y])swap(x,y);
    while(d[x]>d[y])x=f[x][lg[d[x]-d[y]]-1];
    if(x==y)return x;
    for(int i=lg[d[x]];i>=0;--i)
        if(f[x][i]!=f[y][i]){
            x=f[x][i];
            y=f[y][i];
        }
    return f[x][0];
}

int main(){
    ios::sync_with_stdio(false);
    n=read(),m=read();
    for(int i=1,x,y,k;i<=n-1;++i){
        x=read(),y=read(),k=read();
        e[x].push_back({k,y});
        e[y].push_back({k,x});
    }

    for(int i=1;i<=n;++i)
        lg[i]=log(i)/log(2)+1;
    dfs(1,1);

    for(int i=1,x,y;i<=m;++i){
        x=read(),y=read();
        cout<<dis[x]+dis[y]-2*dis[lca(x,y)]<<endl;
    }
    return 0;
}

倍增LCA代码细节有点多，被卡了两发。

1. d[x]>d[y]跳到同一深度之后先判断是不是到一个点了，是就直接返回。

2. 往上跳的时候是f[x][lg[d[x]-d[y]]-1]，因为预处理的时候lg加了1

另外还有一道升级版#2491. 「BJOI2018」求和 - 题目 - LibreOJ (loj.ac)

在洛谷也有收录P4427 [BJOI2018] 求和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

做一题水两边真是太好啦qwq

---

前一题只需要开一个数组dis来维护，这里k的范围有50，所以要开dis[N][51]，来预处理所有深度的k次方，因为要取模所以会用到快速幂，注意根节点1的深度是0，特判返回值。

因为模数比较大别忘了开long long。

快速幂

int qkpow(int a,int k){
    int res=1;
    if(a==0)return 0;//特判0
    while(k){
        if(k&1)res*=a;
        k>>=1;
        a*=a;
        a%=MOD;
        res%=MOD;
    }
    return res;
}

预处理

    //预处理深度i^k次
    for(int i=0;i<N;++i){
        for(int k=1;k<=50;++k){
            a[i][k]= qkpow(i,k);
        }
    }

    d[1]=-1;//这里为-1和我的dfs用法有关
    for(int i=1;i<=n;++i)
        lg[i]=log(i)/log(2)+1;

大法师

void dfs(int now,int fa){
    if(vis[now])return;
    vis[now]=true;
    d[now]=d[fa]+1;
    for(int j=1;j<=50;++j){
        p[now][j]=p[fa][j]+a[d[now]][j];//子节点的j次方前缀和
        p[now][j]%=MOD;
    }
    f[now][0]=fa;
    for(int i=1;i<=lg[d[now]];++i)
        f[now][i]=f[f[now][i-1]][i-1];
    for(auto i:e[now]){
        dfs(i,now);
    }
}

LCA函数部分是一样的就不搬过来了。

这道题是点的前缀和，和前一题边的前缀和不一样。

边和只要减去两倍的LCA就行了，但是点和我们要算上LCA的值，所以是减去LCA和LCA的父节点。

注意

因为最终答案涉及了取模中减法，相减之后可能答案为负数，需要加上MOD再模上MOD。

如果取模中有除法不可轻易使用取模（基本必错），需要使用乘法逆元来计算。

如果递推式使用的是除法并且不会逆元，考虑用加法和减法去递推。

AC代码

#include <bits/stdc++.h>
#define int long long
using namespace std;

inline int read(){
    int x=0;char c=getchar();
    while(c<48 or c>57)c=getchar();
    while(c>=48 and c<=57)x=(x<<3)+(x<<1)+(c xor 48),c=getchar();
    return x;
}

const int N=3e5+5,MOD=998244353;
int n,m,d[N],f[N][20],lg[N],a[N][51],p[N][51];
vector<int>e[N];
bitset<N>vis;

int qkpow(int a,int k){
    int res=1;
    if(a==0)return 0;//特判0
    while(k){
        if(k&1)res*=a;
        k>>=1;
        a*=a;
        a%=MOD;
        res%=MOD;
    }
    return res;
}
void dfs(int now,int fa){
    if(vis[now])return;
    vis[now]=true;
    d[now]=d[fa]+1;
    for(int j=1;j<=50;++j){
        p[now][j]=p[fa][j]+a[d[now]][j];//子节点的j次方前缀和
        p[now][j]%=MOD;
    }
    f[now][0]=fa;
    for(int i=1;i<=lg[d[now]];++i)
        f[now][i]=f[f[now][i-1]][i-1];
    for(auto i:e[now]){
        dfs(i,now);
    }
}
int lca(int x,int y){
    if(d[x]<d[y])swap(x,y);
    while(d[x]>d[y])x=f[x][lg[d[x]-d[y]]-1];
    if(x==y)return x;
    for(int i=lg[d[x]];i>=0;--i)
        if(f[x][i]!=f[y][i]){
            x=f[x][i];
            y=f[y][i];
        }
    return f[x][0];
}

signed main(){
    ios::sync_with_stdio(false);
    n=read();
    for(int i=1,x,y;i<=n-1;++i){
        x=read(),y=read();
        e[x].push_back(y);
        e[y].push_back(x);
    }

    //预处理深度i^k次
    for(int i=0;i<N;++i){
        for(int k=1;k<=50;++k){
            a[i][k]= qkpow(i,k);
        }
    }

    d[1]=-1;
    for(int i=1;i<=n;++i)
        lg[i]=log(i)/log(2)+1;
    dfs(1,1);

    m=read();
    for(int i=1,x,y,k,LCA;i<=m;++i){
        x=read(),y=read(),k=read();
        LCA=lca(x,y);
        cout<<((p[x][k]+p[y][k]-p[LCA][k]-p[f[LCA][0]][k])%MOD+MOD)%MOD<<endl;
        //警惕模运算带来的坑
    }
    return 0;
}