目录
一. 并查集的概念
二. 并查集的模拟实现
2.1 并查集类的声明
2.2 并查集的实现
三. 路径压缩
四. 总结
一. 并查集的概念
在生活中,我们经常需要对某一些事物进行归类处理,即:将N个不同的元素划分为几个互不相交的集合。在初始状态,每个元素都属于一个独立的集合,在归一合并的过程中,经常需要查找某个元素属于哪一个集合,实现上面功能的数据结构,称之为并查集。
举一个生活中的例子,假设小卖部了有如下货物:苹果、香蕉、橘子、面包、薯片、牙膏、毛巾等,一开始进货的时候,这些货物是散装进货的,没有归类。一般而言,我们会将苹果、香蕉、橘子归类为水果,将面包和薯片归为零食,将牙膏和毛巾归为洗漱用品,这就相当于并查集查找元素所属的几何并进行归类的过程。初步归类后,继续将水果和零食统一归类为食物,这相当于合并两个类,并查集可以实现对类的合并。
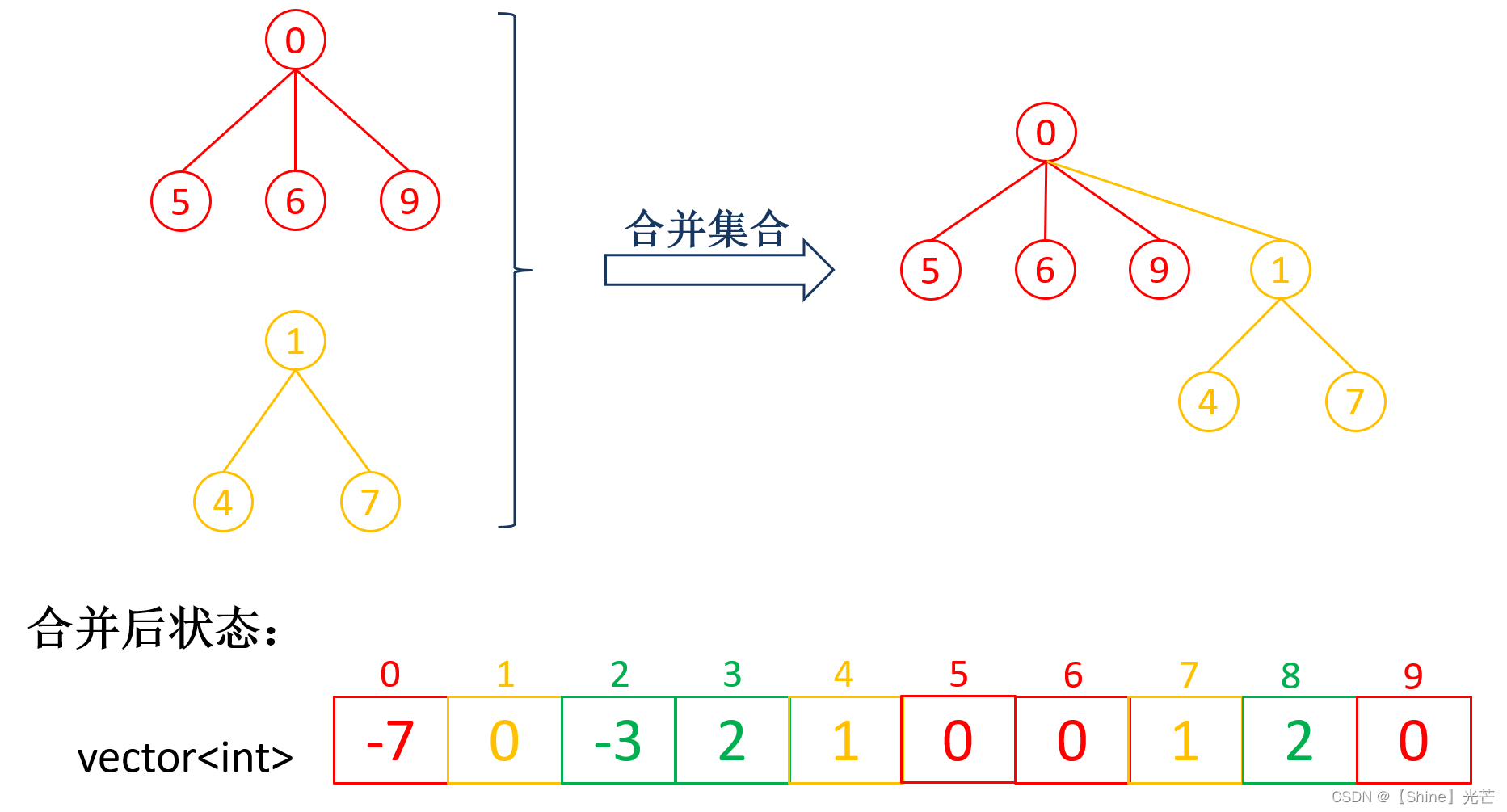
并查集本质上是通过多颗树(森林)来实现的,每一颗树都表示一个独立的集合,使用双亲法表示树结构,即每个节点仅保存其父亲节点。如图1.1所示,将1~9十个数字分为三个集合,分别为{0,5,6,9}、{1,4,7}、{2,3,8},用三棵树表示对应关系,取{...}中第一个数据为根节点,使用vector<int>数组来实现双亲法表示树状结构,假设数据与vector下标直接对应,那么并查集划分集合的过程为:
- 先将vector<int>中每个元素都设为-1,表示每个元素属于独立的集合。
- 开始进行归一化,对于每个叶子节点,查找其根节点,根节点值-1,叶子节点位置处值为其父亲节点的下标。
- 归类完成后,根节点下标处的值为负数,叶子节点下标处的值>=0。
- 对于叶子节点下标处的负数值,设其为rootVal,有:abs(rootVal) = 本集合的数据个数。

如图1.2所示,将图1.1中的{0,5,6,9}和{1,4,7}归为一类,那么1就变为了0的孩子节点,合并后的几集合以0为根节点,有7个元素,因此vector<int>下标为0的位置处元素变为了-1,而原来下标为1的位置处的值变为合并后其父亲节点的值的下标,即0。
二. 并查集的模拟实现
2.1 并查集类的声明
我们假设并查集要管理的元素值从1~N,不考虑模板类型数据和vector<int>下标的映射情况,根据第一节的内容,一个并查集类应当以下成员变量和接口:
- std::vector<int> _ufs :用于以双亲表示法记录每一颗树(每一个集合)。
- 构造函数 :给定数据量,将_ufs中的元素全部初始化为-1。
- int FindRoot(int x),查找元素x所属的根在_ufs中的下标。
- void Union(int x1, int x2) :将x1和x2所在的集合合并为一个集合。
- size_t Size() :统计并查集内集合的个数。
- 析构函数 :采用编译器默认生成的析构函数即可。
代码2.1:并查集类UnionFindSet的声明(UnionFindSet.hpp头文件)
#pragma once
#include <iostream>
#include <vector>
#include <algorithm>
// 并查集
class UnionFindSet
{
public:
UnionFindSet(size_t size);
int FindRoot(int x); // 查找某个元素属于哪个集合(根下标)
void Union(int x1, int x2); // 合并两个集合
size_t Size() const; // 统计并查集内集合的个数
private:
std::vector<int> _ufs;
};2.2 并查集的实现
- 构造函数:给定数据量size,将_ufs初始化为函数size个值为-1的线性表,表示每个元素都属于一个独立的集合。
- 根查找函数int FindRoot(int x):本质上为查找元素属于哪一个集合,前面提到根下标处的元素为负数,因此只需要不断更新x = _ufs[x],直到_ufs[x] < x,然后将x返回即可。
- 集合合并函数void Union(int x1, int x2):先查找两个元素的根root1和root2,如果root1 == root2成立,则表明两个元素属于同一集合,这种情况下直接返回即可。如果root1 != root2,那么就让_ufs[root1] += _ufs[root2],这样根节点下标位置处的绝对值就是集合中元素的个数,然后再执行_ufs[root2] = _ufs[root1],表示跟新被合并集合的根节点。
- 统计集合个数函数size_t Size():统计根节点个数,即_ufs中小于0的元素的个数即可。
代码2.2:并查集的实现(UnionFindSet.cpp源文件)
#define _CRT_SECURE_NO_WARNINGS 1
#include "UnionFindSet.hpp"
UnionFindSet::UnionFindSet(size_t size)
: _ufs(size, -1)
{ }
// 查找某个元素属于哪个集合(根下标)
int UnionFindSet::FindRoot(int x)
{
// 循环查找,直到_ufs[x] < 0
while (_ufs[x] >= 0)
{
x = _ufs[x];
}
return x;
}
// 合并两个集合
void UnionFindSet::Union(int x1, int x2)
{
int root1 = FindRoot(x1);
int root2 = FindRoot(x2);
if (root1 == root2)
{
return;
}
if (root1 > root2)
{
std::swap(root1, root2);
}
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
}
// 统计并查集内集合的个数
size_t UnionFindSet::Size() const
{
// 遍历_ufs统计小于0的元素的个数
size_t count = 0;
for (const auto x : _ufs)
{
if (x < 0) ++count;
}
return count;
}三. 路径压缩
如果并查集中毒元素数量过多,那么每次查找根节点都需要花费较大的成本,那么,就需要采取适当的手段来进行路径压缩。
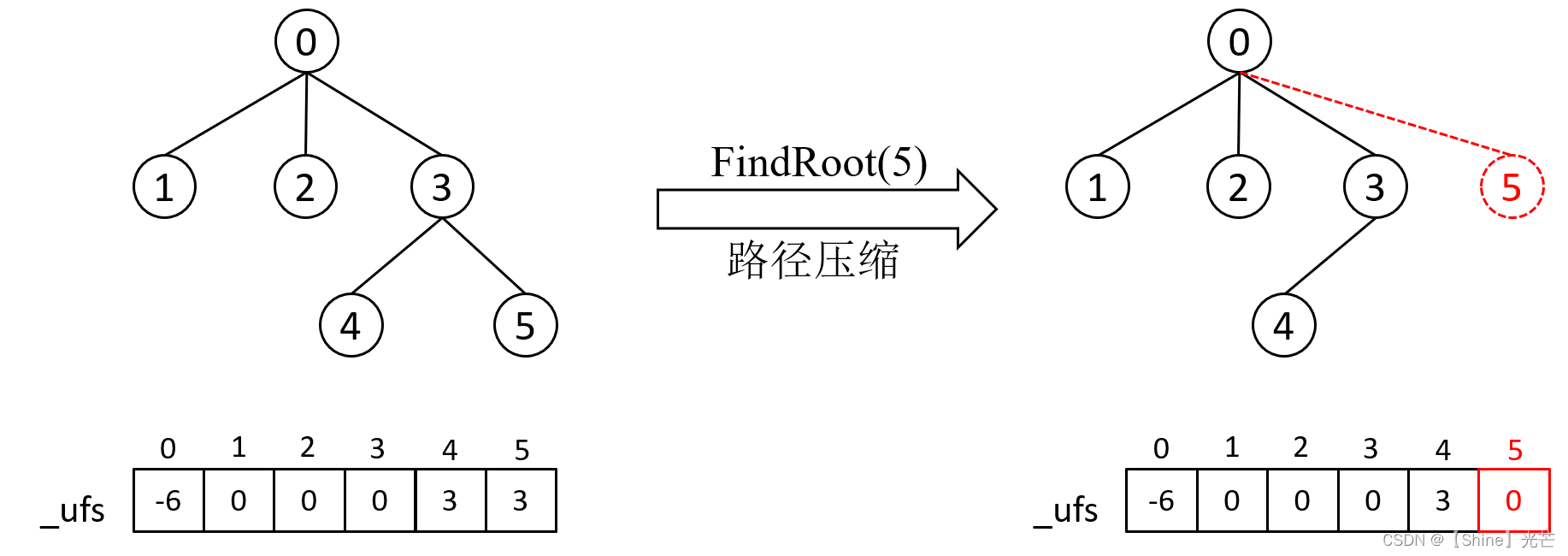
路径压缩最常用的方法:每当查找完一个元素所属集合的根节点后,都将这个元素的父亲节点直接设备根节点,这样当第二次查找这个元素的根节点时,就只需要向上查找一层即可。
如图3.1所示,假设要查找5的根节点,并进行路径压缩,只需要在找到5的根节点0后,将5挂在0的下面即可。当然,如果元素的数量不是很大,就没必要考虑路径压缩,因为路径压缩本身也存在资源消耗。
四. 总结
- 并查集,是通过双签法实现多颗树(森林),来进行数据分类的数据结构。
- 并查集能够实现的功能包括:查找元素所属集合(根节点)、合并集合、统计集合数目。
- 如果并查集中元素的数目过多,那么应当进行路径压缩。