前缀和与差分

当给定一段整数序列a1,a2,a3,a4,a5…an;

每次让我们求一段区间的和，正常做法是for循环遍历区间起始点到结束点，进行求和计算，但是当询问次数很多并且区间很长的时候

比如，10^5 个询问和10^6区间长度，相乘就是 10^11,这样在c++里面会远远的超时，此时我们就要请出一个求区间和的小技巧——前缀和

1 一维前缀和

假设给定一串整数序列 ai= { 1, 2, 3, 4, 5, 6, 7, 8 }

如果我们每次都去求一区间的和，不仅麻烦而且超时

但是我们想，每个数字位置都是固定的，数字总个数也是确定的，这是一个静态的序列

那我们可以先求出前i个数的和，当求区间[ l ,r ]的和时，可以直接由前r个数的和减掉前l个数的和得到的差作为l，r区间的和

有这个思路，那我们可以得到前缀和数组

sum[i] = sum[i-1] + arr[i]; //前i个数的和 = 前i-1个数的和+第i个数的和

ps：我发现有一点点动态规划的味道了

这样就能得到代码了

int n;
cin>>n;
int arr[1000] = {0};
for(int i=1;i<=n;i++)cin>>arr[i];//输入题目给定的整数序列

int sum[1000] = {0};
for(int  i=1;i<=n;i++)sum[i] = sum[i-1]+arr[i];

当我们想输出 l~r 的区间和

可以直接相减得到

即：

cout<<sum[r] - sum[l-1];

原题链接：795. 前缀和 - AcWing题库

完整代码

#include<iostream>

using namespace std;

int n,m;//n个数m次询问
int arr[100100];//输入的整数序列
int sum[100010];//前缀和数组
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>arr[i],sum[i] = sum[i-1]+arr[i];
    while(m--){
        int l,r;
        cin>>l>>r;
        cout<<sum[r]-sum[l-1]<<endl;
       
    }
     return 0;
}

3 二维前缀和

掌握了一位前缀和，根据这个原理，我们就可以很轻松的学习二维前缀和了

现在有一个二维的整数序列，假设我们想计算，（x1,y1)到(x2,y2)矩阵之间的和，即第x1行到x2行之间，第y1列到y2列之间的矩阵和，又该怎么求呢

如果只是二层for循环遍历，那当矩阵大和查询次数多了之后肯定是会超时的，所以这个 方法是肯定不适用的

那么我们的二维前缀和就出场了

二位前缀和数组的使用

首先假设sum[1000] [1000]就是二维前缀和数组，并且我们这是我们已经计算完得到的二维前缀和数组

ps：先讲应用再讲实现方式比较好接受，所以我们先假设二维前缀和数组已经计算完毕了

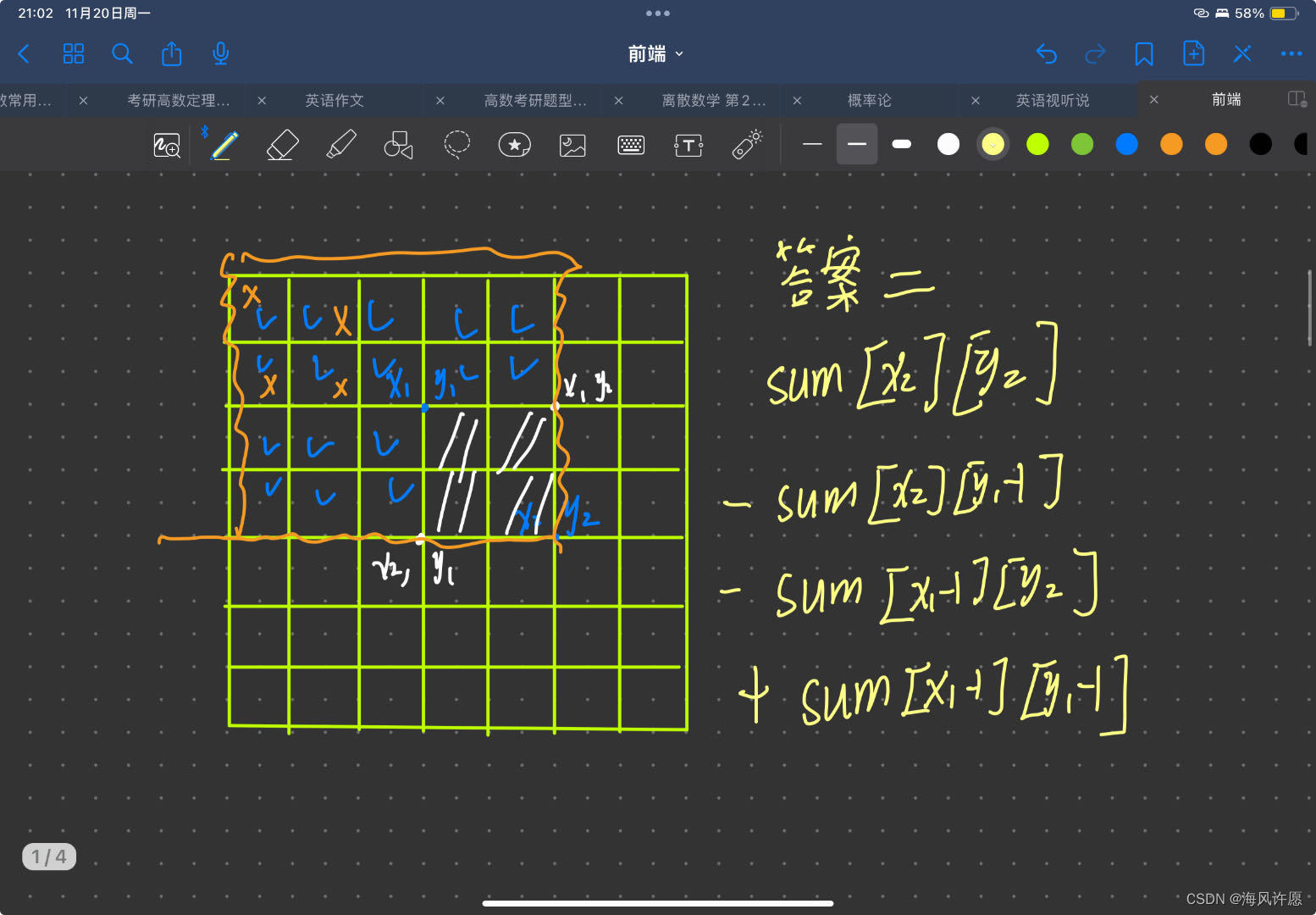
看接下来的图，我们要求(x1,y1)到（x2,y2)之间的矩阵的和，即白色阴影区间的值

sum[x2 ] [y2 ]中保存的是从（0，0）到（x2,y2)矩阵和的值 ，那我们可以通过sum[x2 ] [y2 ] 减去目标区间左边这一块区间的值，再减去上面那一块值，即打勾号的区间，但是我们发现，这两个区间在打×号的地方重合了，也就是多减去了一次，那我们再将这一块加回去，这样就得到的目标区间的值

是不是也很简单

ans = sum[x2][y2] -  sum[x2][y1-1] - sum[x1-1][y2]+sum[x1-1][y1-1];
// sum[x2][y1-1] 左区间
// sum[x1-1][y2] 上区间
// sum[x1-1][y1-1] 重叠区间
// ans 目标区间和

接下来就是二维前缀和数组的构造啦

二维前缀和的构造

已经学习完二维前缀和数组的使用，那我们很已经掌握了整体 - 部分的思想

二维前缀和的构造也使用的这种思路

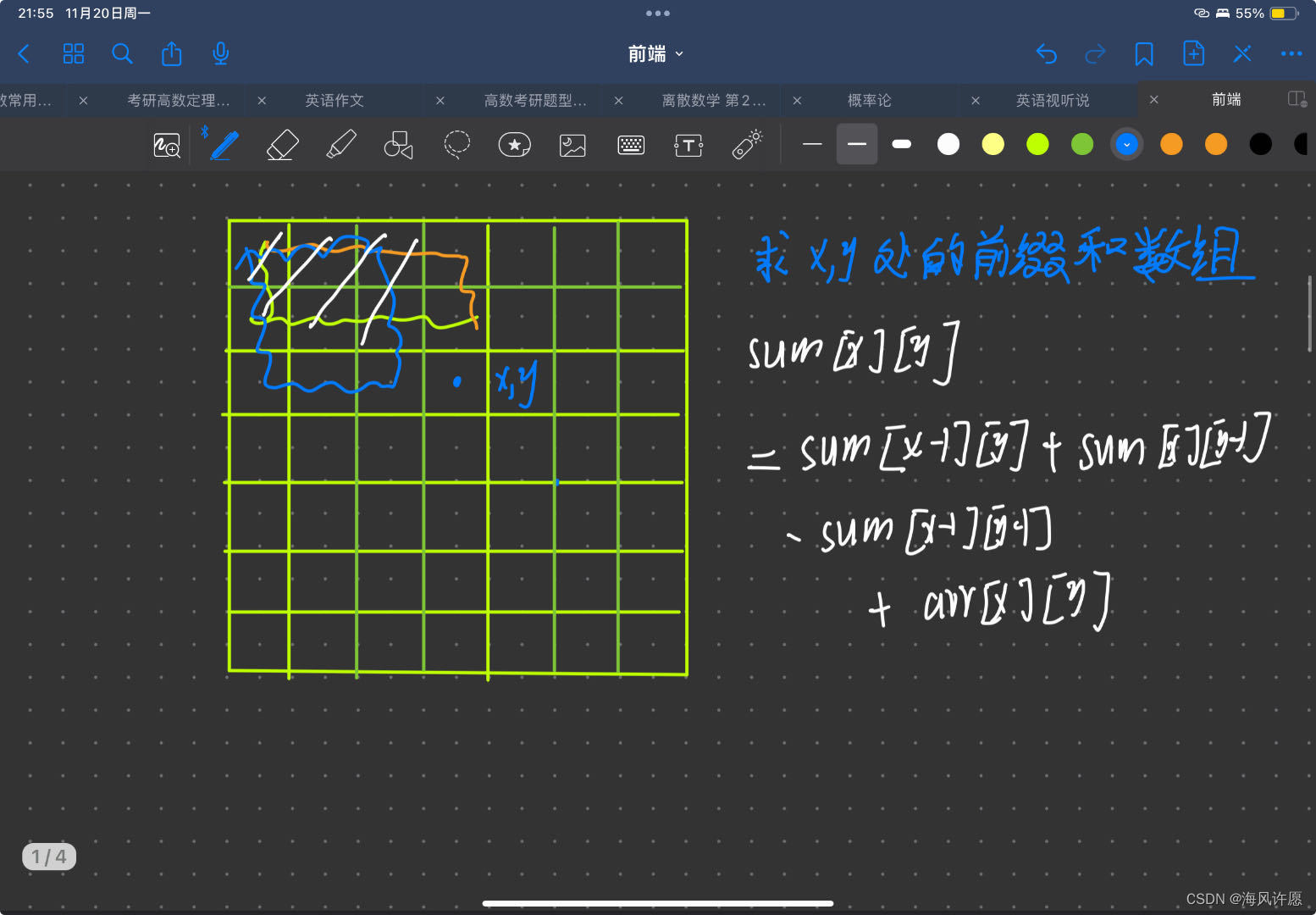
上图！

（x,y)处的前缀和数组可以由（x-1,y）与(x,y-1)两处的计算，但是我们看图会发现，有一部分重叠了，所以需要再减去重叠的(x-1,y-1),再加上这个点的值arr[x] [y]就能得到(x,y)处的前缀和数组

上代码！

sum[x][y] = sum[x-1][y]+sum[x][y-1]-sum[x-1][y-1]+arr[x][y];
//sum[x-1][y] 上面的区间
//sum[x][y-1]左边的区间
//sum[x-1][y-1]重叠区间
//arr[x][y]当前点的值

完整代码：796. 子矩阵的和 - AcWing题库

原题链接：

#include<iostream>

using namespace std;

int n,m,q;
long long int sum[1010][1010];
int main(){
    cin>>n>>m>>q;

    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            int a;
            cin>>a;
            sum[i][j] = sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a;  //得到二维前缀和数组
        }
    }
    while(q--){
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        cout<<sum[x2][y2] - sum[x2][y1-1] - sum[x1-1][y2] + sum[x1-1][y1-1]<<endl;
    }
    return 0;
}

看到这，给个赞再走吧~