【C/C++】递归算法

news2024/9/20 6:42:27

信封

某人写了n封信和n个信封，如果所有的信都装错了信封。求所有的信都装错信封共有多少种不同情况
在这里插入图片描述

#include <iostream>
using namespace std;
const int N = 30;
int n;
long f[N];

int main() {
  scanf("%d", &n);
  f[1] = 0, f[2] = 1;
  for (int i = 3; i <= n; i++)
    f[i] = (i - 1) * (f[i - 1] + f[i - 2]);
  printf("%ld\n", f[n]);
}

求 x^n

设计一个递归函数, 求 x 的 n 次幂; 主函数通过键盘输入 x 和 n 的值，并输出 x^n 的值。(假设 x 为实数, n 为正整数)

#include<stdio.h>

double f(double x,int n){
    if(n==1) return x;
    if(n>1){
        return x*f(x,n-1);
    }
}

int main(){
    double x;
    int n;
    scanf("%lf %d",&x,&n);
    printf("%lf的%d次幂为:%lf\n",x,n,f(x,n));
    return 0;
}

勒让德多项式

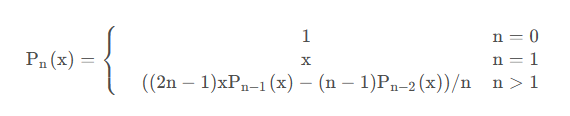
在这里插入图片描述

#include<stdio.h>

double p(int n, double x) {
    if (n == 0) return 1;
    else if (n == 1) return x;
    else if (n > 1) return ((2 * n - 1) * x * p(n - 1, x) - (n - 1) * p(n - 2, x)) / n;
    return 0;
}

int main() {
    int n;
    double x;
    printf("请输入整数 n, 实数 x:\n");
    scanf("%d %lf", &n, &x);
    printf("计算结果是: %lf:\n", p(n, x));
    return 0;
}

切比雪夫多项式

已知：切比雪夫多项式如下：
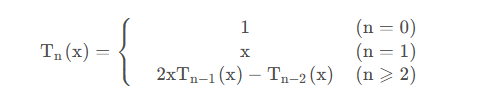
在这里插入图片描述
编写一程序，输入 n，x，并将 0~n u的所有 Tn(x) 的值输出到文件 tdat.txt 中。

#include<stdio.h>

double T(int n, double x) {
    if (n==0) return 1;
    else if(n==1) return x;
    else return 2*x*T(n-1, x) - T(n-2, x);
}

int main() {
    FILE *fp;
   	
    if ((fp = fopen("tdat.txt", "w+")) == NULL) {
        printf("cannot open file\n");
        return 0;
    }
    
    int n;
    double x;
    printf("请输入 n, x 的值: ");
    scanf("%d %lf", &n, &x);
 
    for(int i = 0; i <= n; i++) {
        printf("%d %lf\n", i, T(i,x));
        fprintf(fp, "%d %lf\n", i, T(i, x));
    }
    
    if (fclose(fp) != 0) 
        printf("close file error");
    
    return 0;
}

斐波那契数列

用递归计算斐波那契数列第 n 项，该数列可以表示成：
在这里插入图片描述

#include<stdio.h>

// 斐波那契数列
int fib(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;
    return fib(n - 1) + fib(n - 2);
}

int main() {
    FILE *fp;

    if ((fp = fopen("fab.txt", "w")) == NULL) {
        printf("cannot open file\n");
        return 0;
    }

    int sum = 0;
    for (int i = 1; i <= 20; i++) {
        sum += fib(i);
        printf("%d\n", fib(i));
    }
    printf("sum(1,20) = %d", sum);
    fprintf(fp, "%d", sum);

    if (fclose(fp) != 0)
        printf("close file error");
        
    return 0;
}