---

本文对MATLAB中绘制二维图的常用函数的使用进行例举并给出图示。对函数图的绘制，颜色与线型，坐标范围设置，标题、标签、图例、字体大小等设置做出说明。

绘制一图一线

用法:

plot(x,y); %其中x,y为长度相同的向量，存储x坐标和y坐标

举例：

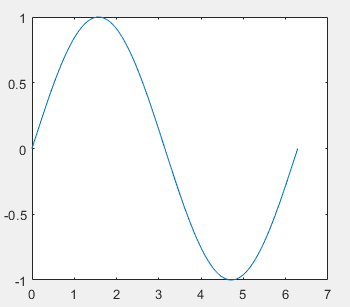
x = 0:2*pi/100:2*pi;%x坐标格式(x = 起始点：间隔：结束点)
y = sin(x);
plot(x,y);

如图：

绘制一图多线

用法一：plot

plot(x,y1,'选项1',x,y2,'选项2',x,y3,'选项三');%选项格式：颜色+线型，如b*、r-、k-o

举例：

x = 0:pi/10:2*pi; %x坐标
y1 = sin(x);      %y坐标1
y2 = cos(x-0.25); %y坐标1
y3 = sin(x-0.5);  %y坐标1

figure;            %新开一个画图窗口
plot(x,y1,'g',x,y2,'b--o',x,y3,'k*');

如图：

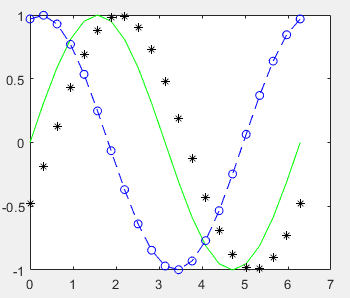
用法二：hold on

hold on;%保留当前坐标区中的绘图，从而使新添加到坐标区中的绘图不会删除现有绘图

举例：

x = linspace(-pi,pi,100); %格式linspace(起始点，结束点，元素个数)
y1 = sin(x);
plot(x,y1);

hold on;
y2 = cos(x);
plot(x,y2);

如图：

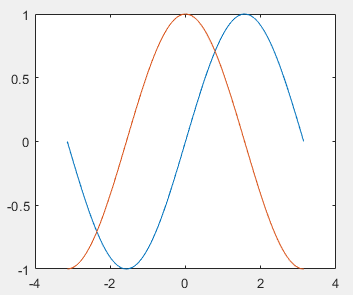
绘制一图多图

用法：

subplot(m,n,p); %将当前图窗划分为 m×n 网格，并在 p 指定的位置创建坐标区。

举例：

%创建一个包含三个子图的图窗。在图窗的上半部分创建两个子图，并在图窗的下半部分创建第三个子图。
subplot(2,2,1); %第一个图
x = linspace(-3.8,3.8);
y_cos = cos(x);
plot(x,y_cos);

subplot(2,2,2); %第二个图
y_poly = 1 - x.^2./2 + x.^4./24;
plot(x,y_poly,'g');

subplot(2,2,[3,4]); %第三四个图
plot(x,y_cos,'b',x,y_poly,'g');

如图：

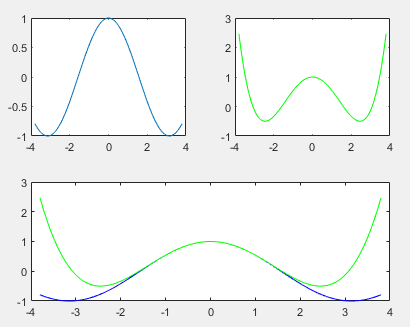
其他形式的坐标图

• 杆图 stem(x,y)
• 条形图 bar(x,y)
• 填充图 fill(x,y)
• 阶梯图 stairs(x,y)
• fill函数按向量元素下标渐增次序依次用直线段连接x，y对应元素定义的数据点。

举例：

x = 0:0.35:7;
y = 2*exp(-0.5*x);
subplot(2,2,1);stem(x,y,'k');
title('stem(x,y,''k'')');axis([0, 7, 0 ,2]);
subplot(2,2,2);bar(x,y,'g');
title('bar(x,y,''g'')');axis([0, 7, 0 ,2]);
subplot(2,2,3);fill(x,y,'r');
title('fill(x,y,''r'')');axis([0, 7, 0 ,2]);
subplot(2,2,4);stairs(x,y,'b');
title('stairs(x,y,''b'')');axis([0, 7, 0 ,2]);

如图：

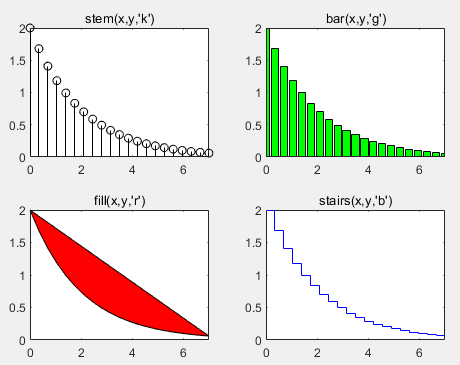
分段函数绘制

方法一：分段写函数的定义域值域

举例：

%分别写出各段的xy
t1=0:0.1:10;
v1=0.5*t1.^2;

t2=10:0.1:20;
v2=2*t2+10;

t3=20:0.1:30;
v3=sin(t3);

%合并xy
t=[t1 t2 t3];
v=[v1 v2 v3];

%画图
plot(t,v);

如图：

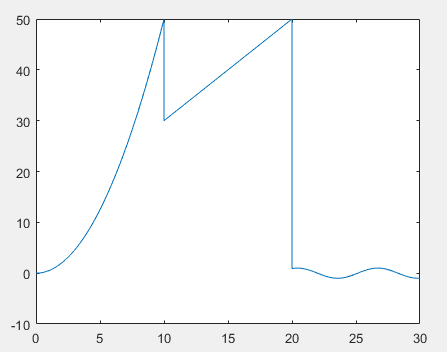
方法二：判断定义域

举例：

%组合函数y=y1.*(x定义域)+y2.*（x定义域）
x=0:0.1:2;
y=x.*(x>=0&x<=1)+(-(x-1).^2+1).*(x>1&x<=2);%括号外是函数，括号内判断为1
plot(x,y);   

如图：

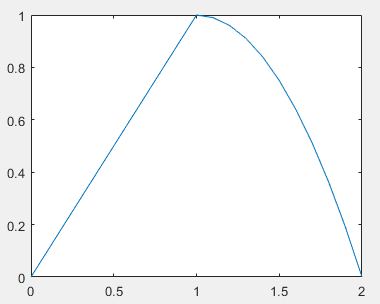
方法三：if else 判断

举例：

t=0:0.01:30;
v=zeros(size(t));
for i=1:length(t)
    if t(i)<=10
         v(i)=0.5*t(i).^2;
    elseif(t(i)>=10)&(t(i)<=20)
         v(i)=2*t(i)+10;
    else
         v(i)=sin(t(i));
    end
end
plot(t,v);

如图：

横纵坐标范围设置

用法一：axis

axis(limits) %limits指定当前坐标区的范围。以包含 4 个元素的向量形式指定范围。

举例：

x = linspace(0,2*pi);
y = sin(x);
plot(x,y,'-o');
axis([0 2*pi -1.5 1.5]);%指定横坐标范围0-2pi，纵坐标范围-1.5-1.5

如图：

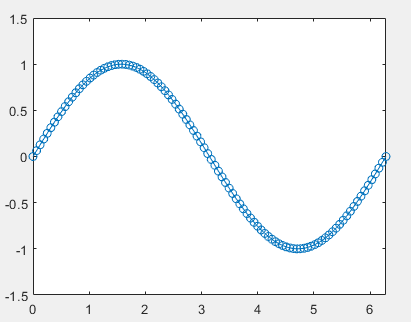
用法二：xlim ylim

xlim([0 2*pi]);%指定横坐标范围
ylim([-1.5 1.5]);%指定纵坐标范围
xlim([-inf 2*pi]);%使用inf自动指定横坐标一边的范围

举例：

x = linspace(0,2*pi);
y = sin(x);
plot(x,y,'-o');
xlim([0 2*pi]);%指定横坐标范围0-2pi
ylim([-1.5 1.5]);%指定纵坐标范围-1.5-1.5

绘制的图和上图一样。

标题、轴标签、图例、字体大小及轴线位置设置

标题：

title('Original Signal');%标题放单引号内

轴标签：

xlabel('X(m)');%横坐标标签放单引号内
ylabel('Y(m)');%纵坐标标签放单引号内

图例：

legend(label1,...,labelN) %设置图例标签。以字符向量或字符串列表形式指定标签，例如 legend('Jan','Feb','Mar')。

字体大小：

title('标题名','FontSize',20)
xlabel('X','FontSize',15)
ylabel('Y','FontSize',10)

轴线位置：

默认情况下，x 轴和 y 轴沿坐标区的外边界显示。通过设置 Axes 对象的 XAxisLocation 和 YAxisLocation 属性来更改轴线位置。将 XAxisLocation 设置为 ‘top’、‘bottom’ 或 ‘origin’。将 YAxisLocation 设置为 ‘left’、‘right’ 或 ‘origin’。这些属性仅适用于二维视图中的坐标区。

ax = gca;
ax.XAxisLocation = 'top';%x轴线位置放于顶处
ax.YAxisLocation = 'right';%y轴线位置放于右边

举例：

x = linspace(-2*pi,2*pi,100);
y1 = sin(x);
y2 = cos(x);
figure;
plot(x,y1,x,y2);%一图两线
xlabel('-2\pi < x < 2\pi');%x轴标签
title('Line Plot of Sine and Cosine Between -2\pi and 2\pi','FontSize',15);%标题
ylabel('Sine and Cosine Values');%y轴标签
legend({'y = sin(x)','y = cos(x)'},'Location','southwest','FontSize',8);%放在左下角

ax = gca;
ax.XAxisLocation = 'origin';%x轴线位置放于原点处
ax.YAxisLocation = 'origin';%y轴线位置放于原点处

如图：

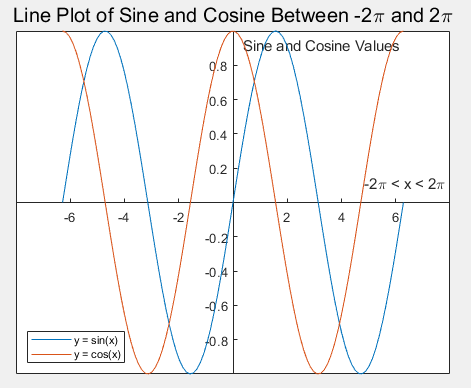
补充

颜色与线型方案

plot(x,y1,'g',x,y2,'b--o',x,y3,'k*');%单引号中选择颜色+线型：如b*、r-、k-o

类型	值	含义
颜色	'c' 'm' 'y' 'r' 'g' 'b' 'w' 'k'	青蓝 品红 黄 红 绿 蓝 白 黑
线型	'-' '--' ':' '-.' 无字符	实线 虚线 点线 点划线 没有线条
标记类型	'+' 'o' '*' 'x' 's' 'd' '^' 'v' '>' '<' 'p' 'h' 无字符	加号 空心圆 星号 字母 x 空心正方形 空心菱形 空心上三角 空心下三角 空心右三角 空心左三角 空心五角形 空心六角形 无标记

点乘和乘的区别

在上面的函数绘制中使用到了*与.*, .^ , ./等运算，其区别如下：

以*与.*为例：

1.1，在进行数值运算和数值乘矩阵时，

这两种没有区别,例如：a*b=a.*b; a*B=a.*B; B*a=B.*a（其中小写字母表示数值，大写字母表示矩阵）

1.2 ，在进行矩阵和矩阵运算时，

*表示普通的矩阵乘法，要求前面矩阵的列数等于后面矩阵的行数；

.*表示两个矩阵对应元素相乘，要求两个矩阵行数列数都相等。

举一反三： /与./ ^与.^ 也是一样的道理。