单/三相dq解耦控制与特定次谐波抑制

news2024/9/23 3:31:48

1. 单相整流器dq坐标系下建模

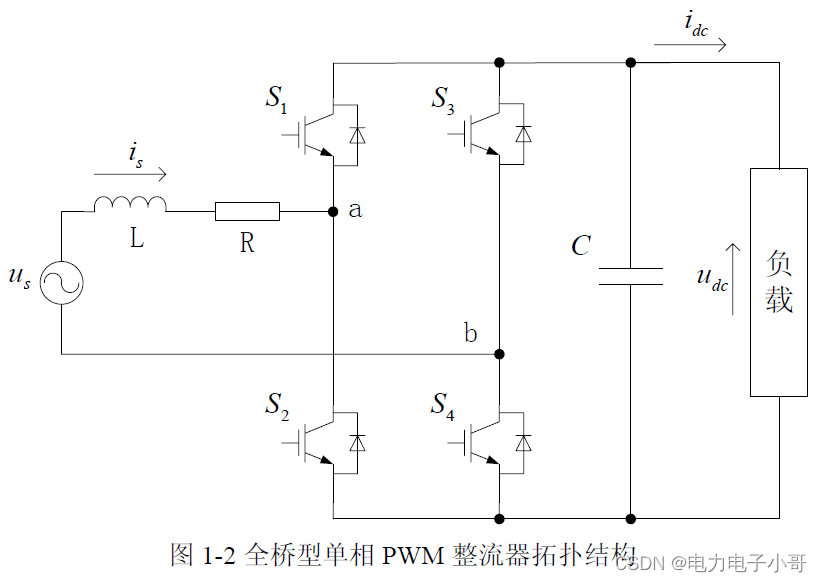
单相整流器的拓扑如图所示，可知 ${u_{ab}} = {u_{s}} - L\frac{{d{i_s}}}{{dt}} - R{i_s}$ 。
将电压和电流写成dq的形式。
$\left\{\begin{array}{l} u_{\mathrm{s}}=U_{\mathrm{sm}} \sin (\omega \mathrm{t}) \\ i_{\mathrm{s}}=I_{\mathrm{d}} \sin (\omega \mathrm{t})+I_{\mathrm{q}} \cos (\omega \mathrm{t}) \\ u_{\mathrm{ab}}=U_{\mathrm{d}} \sin (\omega \mathrm{t})+U_{\mathrm{q}} \cos (\omega \mathrm{t}) \end{array}\right.$
将dq表达式代入 ${u_{ab}} = {u_{s}} - L\frac{{d{i_s}}}{{dt}} - R{i_s}$ 。需要注意的是，Idsin(wt)的求导包含两部分，一部分是对Id求偏导，另一部分是对sinwt求偏导。dq表达式中的其他项也是如此。
最终得到表达式。
$\left\{ \begin{array}{l} {U_d} = {U_{sm}} - L\frac{{d{I_d}}}{{dt}} + {I_q}\omega L - R{I_d}\\ {U_q} = 0 - L\frac{{d{I_q}}}{{dt}} - {I_d}\omega L - R{I_q} \end{array} \right.$ 上述的Ud和Uq是实际值，为了求得目标的Ud和Uq，以d轴为例，需要将PI控制器替代 $L\frac{{d{I_d}}}{{dt}} +R{I_d}$ ，能够得到以下表达式：
$\left\{ \begin{array}{l} L\frac{{d{I_d}}}{{dt}} \approx L\frac{{{I_{dref}} - {I_d}}}{{{T_s}}} = {K_p}({I_{dref}} - {I_d})\\ R{I_d} = \frac{R}{L}\int L{\frac{{d{I_d}}}{{dt}}} dt \approx \frac{R}{L}\int {{K_p}({I_{dref}} - {I_d})} dt = {K_i}\int {({I_{dref}} - {I_d})} dt\\ {K_i} = \frac{R}{L}{K_p} \end{array} \right.$
同理， $L\frac{{d{I_q}}}{{dt}} +R{I_q}$ 也能得到类似的表达式。简单来看就是用PI控制器代替目标的电感电压，由于整流器本质上控制的是端口电压，而端口电压又是和电网电压，电感电压形成矢量三角形的，所以控制电感电压本质上就是控制电感电压。
在这里插入图片描述
将PI的表达式代入Ud和Uq表达式中，得到：
$\left\{\begin{array}{l} U_{d}^{*}=U_{s m}+I_{q} \omega L-K_{p}\left(I_{d r e f}-I_{d}\right)-K_{i} \int\left(I_{d r e f}-I_{d}\right) d t \\ U_{d}^{*}=0-I_{d} \omega L-K_{p}\left(I_{q r e f}-I_{q}\right)-K_{i} \int\left(I_{q r e f}-I_{q}\right) d t \end{array}\right.$
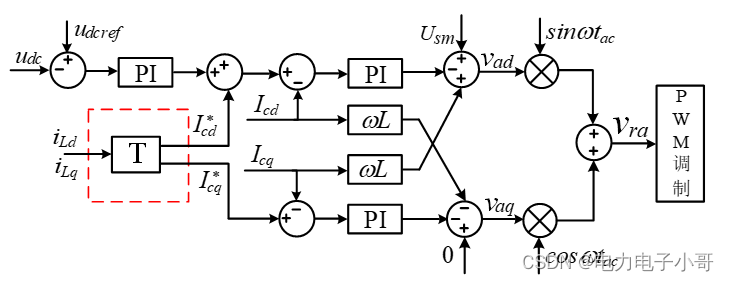
控制框图如图所示。
在这里插入图片描述

2. 单相APFdq坐标系下特定次谐波抑制

单相APF的拓扑如图所示，变换器的目标是补偿电流ic等于iL中谐波电流相反数，由于is=iL+ic，因此is谐波电流为0，由于APF的容量有限，往往仅仅需要补偿低次谐波，就能够达到不错的补偿效果，所以特定次谐波补偿的需求应运而生。
在这里插入图片描述
参考上面的dq解耦控制，可以得到5次谐波抑制的控制表达式，需要注意的是，补偿谐波电流的参考值是负的谐波负载电流，所以 $I_{c5d}$ 的参考值是 $I_{L5d}$ 。
$\left\{\begin{array}{l} U_{5d}^{*}=U_{s m}+I_{c5q} \omega L-K_{p}\left(-I_{L5d}-I_{c5d}\right)+K_{i} \int\left(-I_{L5d}-I_{c5d}\right) d t \\ U_{5q}^{*}=0-I_{c5d} \omega L-K_{p}\left(-I_{L5q}-I_{c5q}\right)+K_{i} \int\left(I_{L5q}+I_{c5q}\right) d t \end{array}\right.$
重新整理表达式，得：
$\left\{\begin{array}{l} U_{5d}^{*}=U_{s m}+I_{c5q} \omega L+K_{p}\left(I_{L5d}+I_{c5d}\right)+K_{i} \int\left(I_{L5d}+I_{c5d}\right) d t \\ U_{5q}^{*}=0-I_{c5d} \omega L+K_{p}\left(I_{L5q}+I_{c5q}\right)+K_{i} \int\left(I_{L5q}+I_{c5q}\right) d t \end{array}\right.$
由于 $U_{s m}$ , $I_{5d} \omega L$ , $I_{5q} \omega L$ 稳态时为常数，并且可以由后面的PI控制器生成，所以实际应用中可以忽略。得到以下表达式：
$\left\{\begin{array}{l} U_{5d}^{*}=K_{p}\left(I_{L5d}+I_{c5d}\right)+K_{i} \int\left(I_{L5d}+I_{c5d}\right) d t \\ U_{5q}^{*}=K_{p}\left(I_{L5q}+I_{c5q}\right)+K_{i} \int\left(I_{L5q}+I_{c5q}\right) d t \end{array}\right.$
再经过dq反变换，得到： $U_5^* = U_{5d}^*\sin (5\omega t) + U_{5d}^*\cos (5\omega t)$ ，将 $U_5^*$ 加入到基波电流控制的调制波中，就能实现谐波补偿的功能。

3. 单相整流器dq坐标系下特定次谐波抑制

单相整流器由于存在直流电压二次纹波，经过调制，从而使电网电流产生3次谐波电流，为了抑制电网电流的3次谐波，可以参考APF的谐波补偿思想，假设负载5次谐波电流为零，则补偿的五次谐波电流参考值为0，从而可得到以下表达式：
$\left\{\begin{array}{l} U_{5d}^{*}=K_{p}\left(0+I_{c5d}\right)+K_{i} \int\left(0+I_{c5d}\right) d t \\ U_{5q}^{*}=K_{p}\left(0+I_{c5q}\right)+K_{i} \int\left(0+I_{c5q}\right) d t \end{array}\right.$
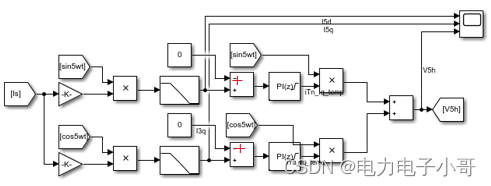
控制框图如图所示，将5次谐波抑制的调制波加入到基波控制器的调制波中，实现了5次谐波电流抑制的功能。
在这里插入图片描述