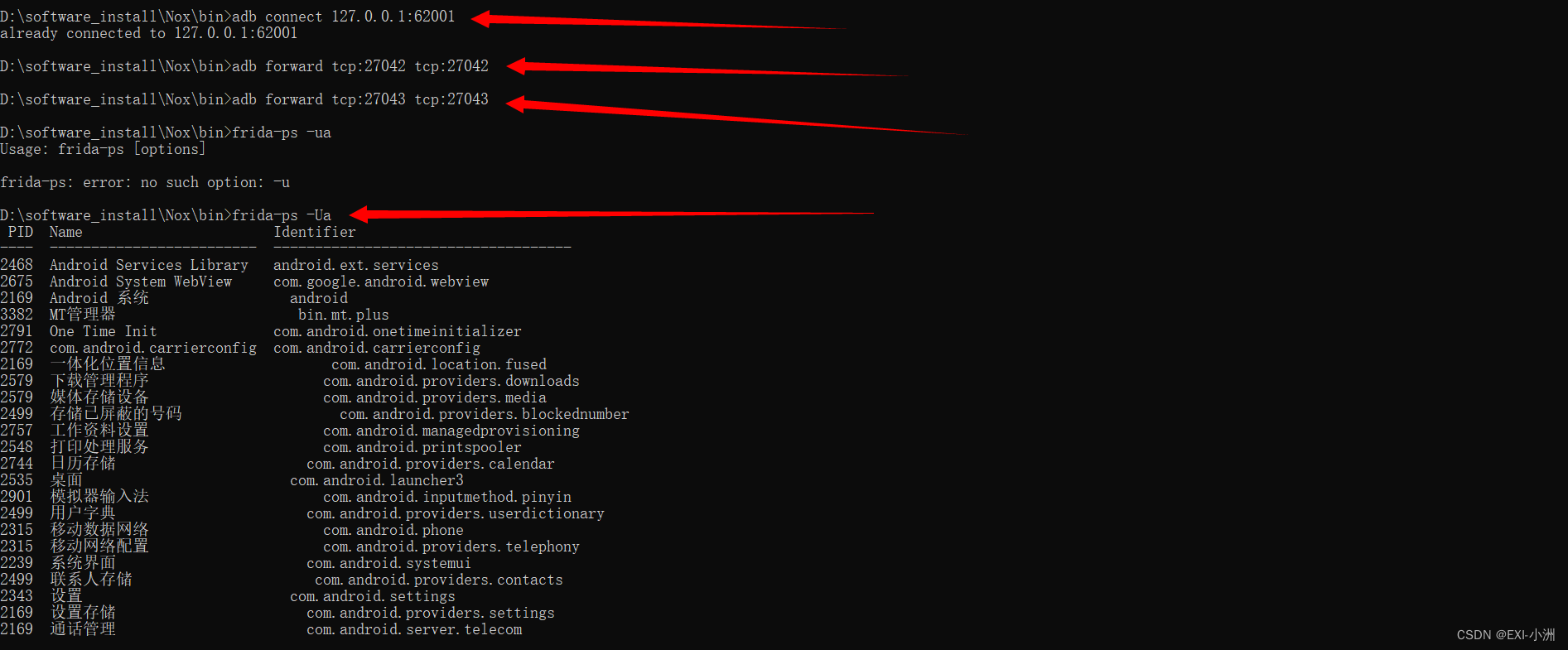
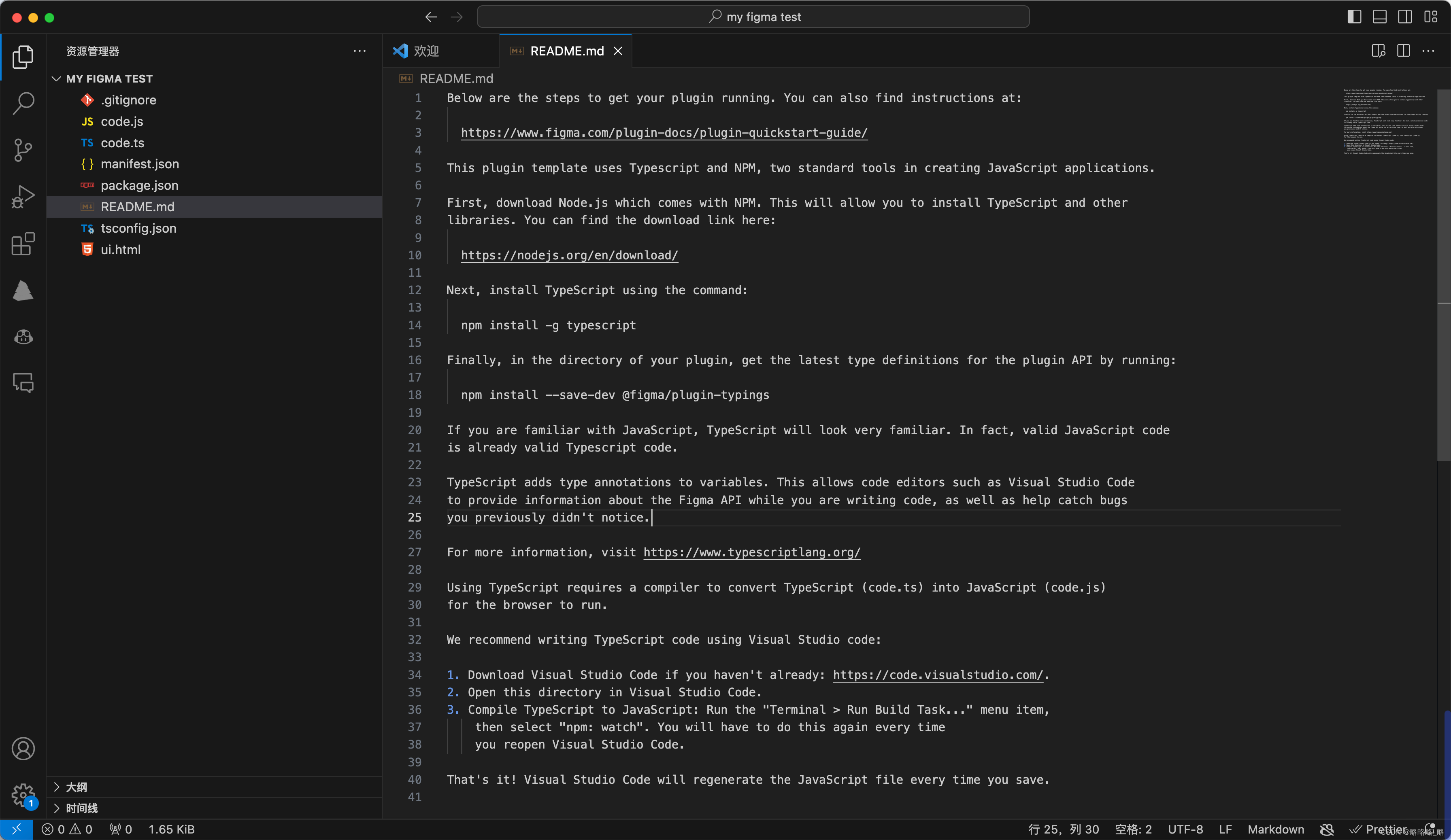
1 文本格式

using System;

namespace Legalsoft.Truffer
{
    /// <summary>
    /// Object for interpolating missing data in a matrix by solving Laplace's
    /// equation.Call constructor once, then solve one or more times
    /// </summary>
    public class Laplace_interp : Linbcg
    {
        private double[,] mat { get; set; }
        private int ii { get; set; }
        private int jj { get; set; }
        private int nn { get; set; }
        private int iter;
        private double[] b;
        private double[] y;
        private double[] mask { get; set; }

        /// <summary>
        /// Values greater than 1.e99 in the input matrix mat are deemed to be missing
        /// data.The matrix is not altered until solve is called.
        /// </summary>
        /// <param name="matrix"></param>
        public Laplace_interp(double[,] matrix)
        {
            this.mat = matrix;
            this.ii = mat.GetLength(0);
            this.jj = mat.GetLength(1);
            this.nn = ii * jj;
            this.iter = 0;
            this.b = new double[nn];
            this.y = new double[nn];
            this.mask = new double[nn];

            double vl = 0.0;
            for (int k = 0; k < nn; k++)
            {
                int i = k / jj;
                int j = k - i * jj;
                if (mat[i, j] < 1.0e99)
                {
                    b[k] = y[k] = vl = mat[i, j];
                    mask[k] = 1;
                }
                else
                {
                    b[k] = 0.0;
                    y[k] = vl;
                    mask[k] = 0;
                }
            }
        }

        /// <summary>
        /// Diagonal preconditioner. (Diagonal elements all unity.)
        /// </summary>
        /// <param name="b"></param>
        /// <param name="x"></param>
        /// <param name="itrnsp"></param>
        public override void asolve(double[] b, double[] x, int itrnsp)
        {
            int n = b.Length;
            for (int i = 0; i < n; i++)
            {
                x[i] = b[i];
            }
        }

        /// <summary>
        /// Sparse matrix, and matrix transpose, multiply.
        /// </summary>
        /// <param name="x"></param>
        /// <param name="r"></param>
        /// <param name="itrnsp"></param>
        public override void atimes(double[] x, double[] r, int itrnsp)
        {
            int n = r.Length;
            double del;
            for (int k = 0; k < n; k++)
            {
                r[k] = 0.0;
            }
            for (int k = 0; k < n; k++)
            {
                int i = k / jj;
                int j = k - i * jj;
                if (mask[k] > 0.0)
                {
                    r[k] += x[k];
                }
                else if (i > 0 && i < ii - 1 && j > 0 && j < jj - 1)
                {
                    if (itrnsp != 0)
                    {
                        r[k] += x[k];
                        del = -0.25 * x[k];
                        r[k - 1] += del;
                        r[k + 1] += del;
                        r[k - jj] += del;
                        r[k + jj] += del;
                    }
                    else
                    {
                        r[k] = x[k] - 0.25 * (x[k - 1] + x[k + 1] + x[k + jj] + x[k - jj]);
                    }
                }
                else if (i > 0 && i < ii - 1)
                {
                    if (itrnsp != 0)
                    {
                        r[k] += x[k];
                        del = -0.5 * x[k];
                        r[k - jj] += del;
                        r[k + jj] += del;
                    }
                    else
                    {
                        r[k] = x[k] - 0.5 * (x[k + jj] + x[k - jj]);
                    }
                }
                else if (j > 0 && j < jj - 1)
                {
                    if (itrnsp != 0)
                    {
                        r[k] += x[k];
                        del = -0.5 * x[k];
                        r[k - 1] += del;
                        r[k + 1] += del;
                    }
                    else
                    {
                        r[k] = x[k] - 0.5 * (x[k + 1] + x[k - 1]);
                    }
                }
                else
                {
                    int jjt = i == 0 ? jj : -jj;
                    int it = j == 0 ? 1 : -1;
                    if (itrnsp != 0)
                    {
                        r[k] += x[k];
                        del = -0.5 * x[k];
                        r[k + jjt] += del;
                        r[k + it] += del;
                    }
                    else
                    {
                        r[k] = x[k] - 0.5 * (x[k + jjt] + x[k + it]);
                    }
                }
            }
        }

        /// <summary>
        /// Invoke Linbcg::solve with appropriate arguments.The default argument
        /// values will usually work, in which case this routine need be called only
        /// once. The original matrix mat is refilled with the interpolated solution.
        /// </summary>
        /// <param name="tol"></param>
        /// <param name="itmax"></param>
        /// <returns></returns>
        public double solve(double tol = 1.0e-6, int itmax = -1)
        {
            double err = 0.0;
            if (itmax <= 0)
            {
                itmax = 2 * Math.Max(ii, jj);
            }
            solve( b,  y, 1, tol, itmax, ref iter, ref err);
            for (int k = 0, i = 0; i < ii; i++)
            {
                for (int j = 0; j < jj; j++)
                {
                    mat[i, j] = y[k++];
                }
            }
            return err;
        }
    }
}
 

2 代码格式

using System;

namespace Legalsoft.Truffer
{
    /// <summary>
    /// Object for interpolating missing data in a matrix by solving Laplace's
    /// equation.Call constructor once, then solve one or more times
    /// </summary>
    public class Laplace_interp : Linbcg
    {
        private double[,] mat { get; set; }
        private int ii { get; set; }
        private int jj { get; set; }
        private int nn { get; set; }
        private int iter;
        private double[] b;
        private double[] y;
        private double[] mask { get; set; }

        /// <summary>
        /// Values greater than 1.e99 in the input matrix mat are deemed to be missing
        /// data.The matrix is not altered until solve is called.
        /// </summary>
        /// <param name="matrix"></param>
        public Laplace_interp(double[,] matrix)
        {
            this.mat = matrix;
            this.ii = mat.GetLength(0);
            this.jj = mat.GetLength(1);
            this.nn = ii * jj;
            this.iter = 0;
            this.b = new double[nn];
            this.y = new double[nn];
            this.mask = new double[nn];

            double vl = 0.0;
            for (int k = 0; k < nn; k++)
            {
                int i = k / jj;
                int j = k - i * jj;
                if (mat[i, j] < 1.0e99)
                {
                    b[k] = y[k] = vl = mat[i, j];
                    mask[k] = 1;
                }
                else
                {
                    b[k] = 0.0;
                    y[k] = vl;
                    mask[k] = 0;
                }
            }
        }

        /// <summary>
        /// Diagonal preconditioner. (Diagonal elements all unity.)
        /// </summary>
        /// <param name="b"></param>
        /// <param name="x"></param>
        /// <param name="itrnsp"></param>
        public override void asolve(double[] b, double[] x, int itrnsp)
        {
            int n = b.Length;
            for (int i = 0; i < n; i++)
            {
                x[i] = b[i];
            }
        }

        /// <summary>
        /// Sparse matrix, and matrix transpose, multiply.
        /// </summary>
        /// <param name="x"></param>
        /// <param name="r"></param>
        /// <param name="itrnsp"></param>
        public override void atimes(double[] x, double[] r, int itrnsp)
        {
            int n = r.Length;
            double del;
            for (int k = 0; k < n; k++)
            {
                r[k] = 0.0;
            }
            for (int k = 0; k < n; k++)
            {
                int i = k / jj;
                int j = k - i * jj;
                if (mask[k] > 0.0)
                {
                    r[k] += x[k];
                }
                else if (i > 0 && i < ii - 1 && j > 0 && j < jj - 1)
                {
                    if (itrnsp != 0)
                    {
                        r[k] += x[k];
                        del = -0.25 * x[k];
                        r[k - 1] += del;
                        r[k + 1] += del;
                        r[k - jj] += del;
                        r[k + jj] += del;
                    }
                    else
                    {
                        r[k] = x[k] - 0.25 * (x[k - 1] + x[k + 1] + x[k + jj] + x[k - jj]);
                    }
                }
                else if (i > 0 && i < ii - 1)
                {
                    if (itrnsp != 0)
                    {
                        r[k] += x[k];
                        del = -0.5 * x[k];
                        r[k - jj] += del;
                        r[k + jj] += del;
                    }
                    else
                    {
                        r[k] = x[k] - 0.5 * (x[k + jj] + x[k - jj]);
                    }
                }
                else if (j > 0 && j < jj - 1)
                {
                    if (itrnsp != 0)
                    {
                        r[k] += x[k];
                        del = -0.5 * x[k];
                        r[k - 1] += del;
                        r[k + 1] += del;
                    }
                    else
                    {
                        r[k] = x[k] - 0.5 * (x[k + 1] + x[k - 1]);
                    }
                }
                else
                {
                    int jjt = i == 0 ? jj : -jj;
                    int it = j == 0 ? 1 : -1;
                    if (itrnsp != 0)
                    {
                        r[k] += x[k];
                        del = -0.5 * x[k];
                        r[k + jjt] += del;
                        r[k + it] += del;
                    }
                    else
                    {
                        r[k] = x[k] - 0.5 * (x[k + jjt] + x[k + it]);
                    }
                }
            }
        }

        /// <summary>
        /// Invoke Linbcg::solve with appropriate arguments.The default argument
        /// values will usually work, in which case this routine need be called only
        /// once. The original matrix mat is refilled with the interpolated solution.
        /// </summary>
        /// <param name="tol"></param>
        /// <param name="itmax"></param>
        /// <returns></returns>
        public double solve(double tol = 1.0e-6, int itmax = -1)
        {
            double err = 0.0;
            if (itmax <= 0)
            {
                itmax = 2 * Math.Max(ii, jj);
            }
            solve( b,  y, 1, tol, itmax, ref iter, ref err);
            for (int k = 0, i = 0; i < ii; i++)
            {
                for (int j = 0; j < jj; j++)
                {
                    mat[i, j] = y[k++];
                }
            }
            return err;
        }
    }
}