前期知识 & 相关链接

树形DP：监控二叉树【基础算法精讲 25】

---

相关链接：
【算法】树形DP ①（树的直径）
【算法】树形DP ② 打家劫舍Ⅲ（树上最大独立集）

本文中的四道题目都很重要！

例题

968. 监控二叉树

https://leetcode.cn/problems/binary-tree-cameras/solutions/2452795/shi-pin-ru-he-si-kao-shu-xing-dpgai-chen-uqsf/

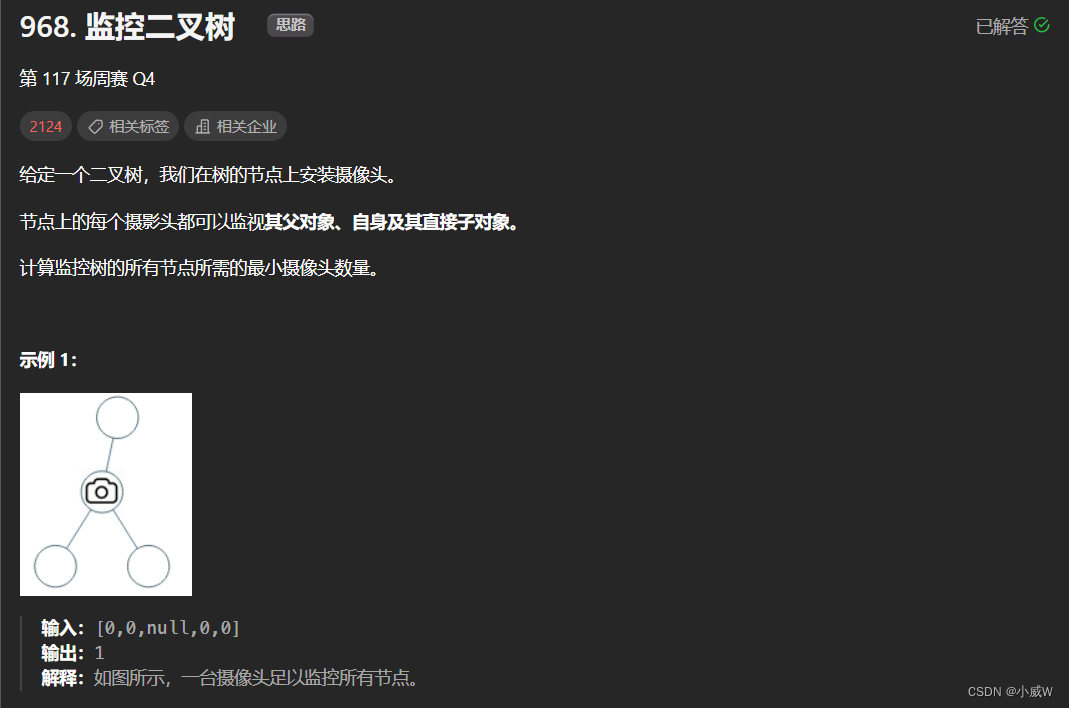
提示：
给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。

解法1——标记状态+贪心

从下到上dfs，标记各个节点的节点。必须使用时就使用一个监控。

class Solution {
    int ans = 0;

    public int minCameraCover(TreeNode root) {
        if (dfs(root) == 0) ans++;
        return ans;
    }

    // 0没有被覆盖，1被覆盖，使用摄像头2
    public int dfs(TreeNode root) {
        if (root == null) return 1;
        int l = dfs(root.left), r = dfs(root.right);
        if (l == 0 || r == 0) {
            ans++;
            return 2;
        } else if (l == 2 || r == 2) return 1;
        return 0;
    }
}

解法2——动态规划

同样是后序dfs。
状态分为：该节点上有，该节点父节点上有，该节点子节点上有。
dp 中的数值 表示 花费。

class Solution {
    public int minCameraCover(TreeNode root) {
        int[] res = dfs(root);
        return Math.min(res[0], res[2]);
    }

    // 该节点上有，该节点父节点上有，该节点子节点上有
    public int[] dfs(TreeNode root) {
        if (root == null) {
            return new int[]{Integer.MAX_VALUE / 2, 0, 0};
        }
        int[] l = dfs(root.left), r = dfs(root.right);
        int choose = Math.min(l[0], l[1]) + Math.min(r[0], r[1]) + 1;   // 自己选
        int byFa = Math.min(l[0], l[2]) + Math.min(r[0], r[2]);         // 自己不选，用他爹的
        int byChildren = Math.min(Math.min(l[0] + r[2], l[2] + r[0]), l[0] + r[0]);	// 自己不选，用它儿子的
        return new int[]{choose, byFa, byChildren};
    }
}

相关练习题目

P2458 [SDOI2006] 保安站岗⭐（有多个儿子节点）🚹

https://www.luogu.com.cn/problem/P2458

将节点分成三类：1.靠自己 2.靠父节点 3.靠子节点。

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt(), root = 0;
        int[] cost = new int[n + 1];
        List<Integer>[] g = new ArrayList[n + 1];
        Arrays.setAll(g, e -> new ArrayList<>());
        for (int i = 2; i <= n + 1; ++i) {
            int x = scanner.nextInt(), c = scanner.nextInt(), m = scanner.nextInt();
            if (root == 0) root = x;    // 记录根节点标号
            cost[x] = c;
            for (int j = 0; j < m; ++j) {
                int y = scanner.nextInt();
                g[x].add(y);
            }
        }
        int[] res = dfs(root, g, cost);
        System.out.println(Math.min(res[0], res[2]));
    }

    // 自己，父节点，儿子
    public static int[] dfs(int x, List<Integer>[] g, int[] cost) {
        int c = cost[x], fa = 0, ch = Integer.MAX_VALUE;
        for (int y: g[x]) {
            int[] res = dfs(y, g, cost);
            c += Math.min(res[0], res[1]);      // 靠自己：从靠自己和靠爹的转移过来
            fa += Math.min(res[0], res[2]);     // 靠爹：从靠自己和靠儿子的转移过来
            ch = Math.min(ch, res[0] - res[2]); // 靠儿子：子节点不可能靠爹，且至少有一个靠自己.这里处理最少一个靠自己，最后再加上fa
        }
        return new int[]{c, fa, fa + Math.max(0, ch)};
    }
}

主要考虑递推公式的写法。
其中靠儿子的转移：子节点不可能靠爹，且至少有一个靠自己。先去掉这个“至少有一个靠自己”的限制条件，那么 ch 的计算就和 fa 的计算一样了。除此之外，我们要记录 res[0] - res[2] 的最小值，这样最后将其和 0 取最大值，就可以达到将至少一个靠儿子的节点修改成靠自己的节点了。

LCP 34. 二叉树染色⭐（每个节点 单独dp[k + 1]数组）

https://leetcode.cn/problems/er-cha-shu-ran-se-UGC/description/

提示：
1 <= k <= 10
1 <= val <= 10000
1 <= 结点数量 <= 10000

参考题解：https://leetcode.cn/problems/er-cha-shu-ran-se-UGC/solutions/1427646/by-codesheng-n-ewdf/

后序遍历。

对于每个节点，都有一个 dp[k + 1] 的数组，其中dp[i]表示到该节点连续有i个时的最大价值。

class Solution {
    public int maxValue(TreeNode root, int k) {
        return dfs(root, k)[k];
    }

    public int[] dfs(TreeNode root, int k) {
        if (root == null) return new int[k + 1];
        int[] dp = new int[k + 1];
        int[] l = dfs(root.left, k), r = dfs(root.right, k);
        // dp数组初始化
        dp[0] = l[k] + r[k];    // 当前节点不选
        // 枚举与当前节点连续的节点数量
        for (int i = 1; i <= k; ++i) {
            dp[i] = dp[i - 1];
            // 枚举左右子树的分配情况
            for (int j = 0; j < i; ++j) {
                dp[i] = Math.max(dp[i], l[j] + r[i - j - 1] + root.val);
            }
        }
        return dp;
    }
}

LCP 64. 二叉树灯饰⭐⭐⭐⭐⭐

https://leetcode.cn/problems/U7WvvU/description/

提示：
1 <= 节点个数 <= 10^5
0 <= Node.val <= 1

https://leetcode.cn/problems/U7WvvU/solutions/1846995/shu-xing-dp-by-endlesscheng-isuo/

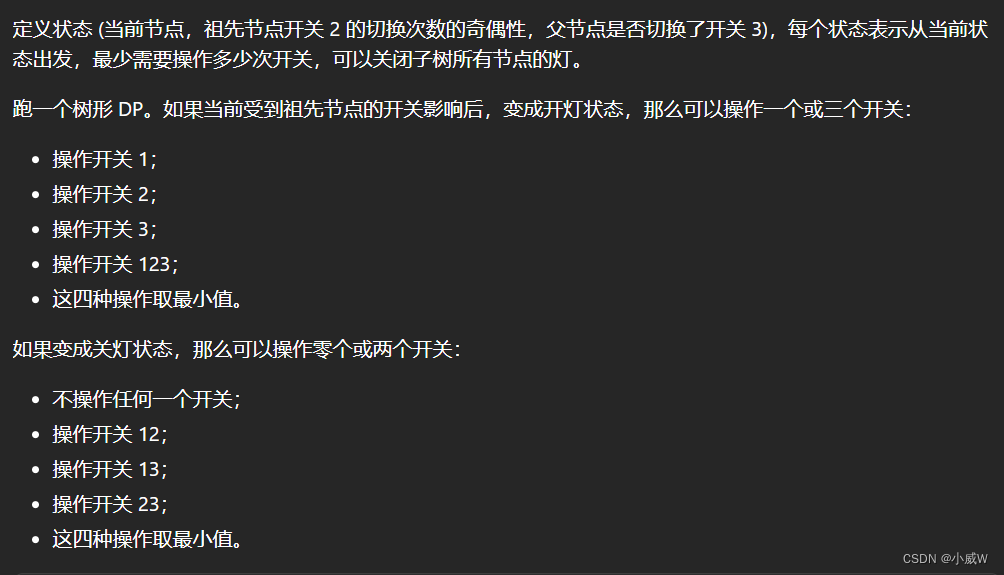
代码按照记忆化搜索来写。Java要用TreeNode当数组下标可以通过Map来实现。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    Map<TreeNode, int[][]> map;

    public int closeLampInTree(TreeNode root) {
        map = new HashMap<>();
        // 当前节点，祖先节点开关2的奇偶性，父节点是否切换了开关3
        return dfs(root, false, false);
    }

    public int dfs(TreeNode node, boolean s2, boolean s3) {
        if (node == null) return 0;
        int x = s2? 1: 0, y = s3? 1: 0;
        int[][] val = new int[2][2];
        if (map.containsKey(node)) {
            val = map.get(node);
            if (val[x][y] > 0) return val[x][y];
        } else {
            map.put(node, val);
        }

        if ((node.val == 1) == (s2 == s3)) {
            // 需要从开灯变成关灯状态
            int res1 = dfs(node.left, s2, false) + dfs(node.right, s2, false)+ 1;
            int res2 = dfs(node.left, !s2, false) + dfs(node.right, !s2, false) + 1;
            int res3 = dfs(node.left, s2, true) + dfs(node.right, s2, true) + 1;
            int res4 = dfs(node.left, !s2, true) + dfs(node.right, !s2, true) + 3;
            val[x][y] = min(res1, res2, res3, res4);
        } else {
            // 需要保持关灯状态
            int res1 = dfs(node.left, s2, false) + dfs(node.right, s2, false);
            int res2 = dfs(node.left, !s2, false) + dfs(node.right, !s2, false) + 2;
            int res3 = dfs(node.left, s2, true) + dfs(node.right, s2, true) + 2;
            int res4 = dfs(node.left, !s2, true) + dfs(node.right, !s2, true) + 2;
            val[x][y] = min(res1, res2, res3, res4);
        }
        return val[x][y];
    }

    public int min(int a, int b, int c, int d) {
        if (b < a) a = b;
        if (c < a) a = c;
        if (d < a) a = d;
        return a;
    }
}

代码耗时 672 ms。