各位同学好,今天我和大家分享一下python机器学习中的特征选择和数据降维。内容有:
(1)过滤选择;(2)数据降维PCA;(3)sklearn实现
那我们开始吧。
一个数据集中可能会有以下问题:
(1)冗余:部分特征的相关度高,由于A与B之间有某种计算公式使它们相关联,A特征的变化会导致B特征的变化,容易消耗计算性能,只需要存在一个特征就可以了。
(2)噪声:部分特征对预测结果有负影响,需要剔除一些与预测对象不相关的特征。
理解特征选择: 现在有一个数据集,这个数据集中有100个特征,我们只需要其中的几十项,这时我们需要对这个数据集进行选择。
理解数据降维: 现在有一个数据集,数据集中有100列特征,也叫做有100个维度,通过降维将数据将到几十维。降维时,一般会改变原维度所代表的意义。例如,现在有A、B两个维度,给它降到一维,称之为C,而C维度代表的意义是同时代表A、B维度的新维度。
1. 特征选择
特征选择是单纯地从提取到的所有特征中选择部分特征作为训练集特征,特征在选择前和选择后可以改变值,也可以不改变值。但是选择后的特征维数肯定比选择前小,毕竟我们只选择了其中的一部分特征。
特征选择分为三种方式:
(1)Filter(过滤式): 根据方差、阈值选择
(2)Embedded(嵌入式): 正则化、决策树
(3)Wrapper(包裹式): 不常用
2. 过滤选择
过滤式的特征选择是根据方差选择,它会删除所有低方差的特征,默认会删除所有方差为0的数据。可以使用sklearn中的 VarianceThreshold(threshold=0) 方差、阈值来实现过滤。若该列的方差小于我指定的阈值,就会删除该特征列。
方差的大小可以体现数据的离散程度。方差越小,说明数据越集中,这个数据对整个结果的影响并不大,所以优先删除方差等于0或接近0的特征。
比如,当方差等于0时,表示该特征列上所有的值都是一样的,一列数据都是一样的对预测结果毫无关系,这时就可以把这一列删除。如果方差较大,该特征列的离散程度也比较大,对结果会有比较大的影响。
在sklearn中实现,导入方法: from sklearn.feature_selection import VarianceThreshold
方差、阈值过滤方法: VarianceThreshold()
参数设置: threshold: 阈值默认等于0;方差小于该阈值时删除该特征列。
# 特征选择
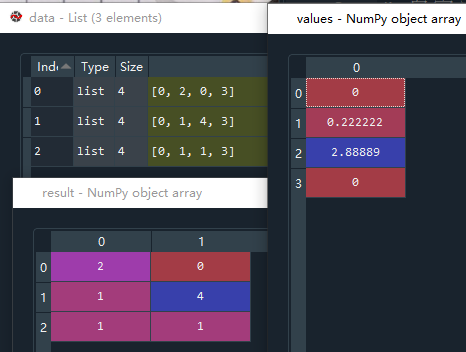
# 自定义数据,第0列和3列的值都是一样的
data = [[0,2,0,3],[0,1,4,3],[0,1,1,3]]
# 导入标准化方法,查看每一列的方差
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit_transform(data)
# 查看方差
values = scaler.var_
# 导入过滤选择方法
from sklearn.feature_selection import VarianceThreshold
# 接收过滤选择方法
var = VarianceThreshold()
# 将数据传入方差、阈值过滤方法,将方差为0的特征删除
result = var.fit_transform(data)
首先使用标准化方法查看每一项特征值的方差 scaler.var_ 便于对数据的每个特征值的方差有了解,再使用过滤选择方法,默认删除方差为0的特征列。
3. PCA(主成分分析)
3.1 方法介绍
主成分分析是一种统计方法,是数据降维中的一种,通过正交变换将一组可能存在相关性的变量转换为一组线形不相关的变量,转换后的这组变量叫主成分。
在用主成分分析方法研究多变量问题时,变量个数太多会增加课题的复杂性。人们希望变量的个数减少而得到的信息较多。在很多情形下,变量之间有一定的相关关系。当两个变量之间有一定的相关关系时,可以解释为,这两个变量反映此课题的信息有一定的重叠。
主成分分析是对原先提出的所有变量,将重复的变量(关系紧密的变量删去多余),建立尽可能少的新变量,使得这些新变量是两两不相关的,而且这些新变量在反映课题的信息反面尽可能保持原有的信息。
3.2 主成分分析求解步骤
(1)获取方差最大的正交变换

上图中蓝色坐标轴是原来数据的坐标轴,坐标上有一个点(2,2);经过变换后得到红色坐标轴,这个点的位置没有发生改变,但是点的坐标变化了;这样就可以将我们的数据变成另外一个值了。
但是这个正交变化该怎么变?我们是通过方差来决定的,也就是正交变换完后,哪个方差最大,那么就选哪个。方差越大,代表数据越不集中,对结果的影响也越大。变换公式如下:
pi 代表正交变换参数,ai代表每一条数据的特征,如果求完后的结果的方差是最大的,那么就选择该组正交变化参数p
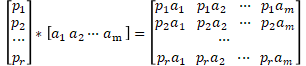
3.3 生成更多主成分
以上是生成一个主成分(新特征)的步骤。一般我们会生成多个主成分,必须遵循一个条件,也就是多个主成分之间不能存在线形相关,即特征之间不能通过某种公式来互相转换。用数学公式来表示则为协方差:
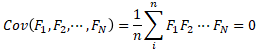
(1)降维后的特征之间的协方差为0,表示各个特征关系是独立的,每个特征都不会随着其他特征变化而有规律的变化。
(2)如果两个特征之间相关联,那么这个两个的协方差较大。新生成一个主成分需要和原来的主成分求一下协方差,如果为0,证明可行。
(3)新生成的主成分的每个特征的方差应该尽可能大。
3.4 sklearn 实现 PCA
导入方法: from sklearn.decomposition import PCA
降维方法: PCA() 参数设置
n_components:
(1)0-1之间,维度的比例再减1。例:若原数组有4个特征列,指定n_components=0.9,代表原来有4维,现在变成4*0.9=3.6,取整数部分,现在有3维,再减1维。最终降到2维。
(2)整型数据。具体维度,不能指定超过当前 min{行数,列数} 的维度。
# PCA
# 自定义数据
data = [[4,2,76,9],[1,192,1,56],[34,5,20,90]]
# 导入方法
from sklearn.decomposition import PCA
# 构建PCA对象,默认降低一个维度
pca = PCA(n_components=0.9)
# 数据传入PCA方法
result = pca.fit_transform(data)