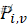基于EKF的传感器融合定位(Python仿真)
- 简述
- 1. 背景介绍
- 1.1. EKF扩展卡尔曼滤波
- 1.1.1.概念
- 1.1.2. 扩展卡尔曼滤波的主要步骤如下:
- 1.1.3. 优、缺点
- 1.2. 航位推算
- 1.3. 目前航位算法的使用通常与卡尔曼滤波相结合使用
- 2. 分段代码
- 2.1. 导入需要的包
- 2.2. 设置相关参数
- 2.3. 输入
- 2.4. 噪声添加
- 2.5. 运动模型
- 2.6. 观测模型
- 2.7. 雅可比(Jacobian)运动模型
- 2.8. 扩展卡尔曼滤波估计模型
- 2.8.1. 预测
- 2.9. 计算并绘制EKF协方差椭圆
- 2.10. 主函数
- 3. 代码运行结果展示与分析
- 3.1. 实验结果展示
- 3.2. EKF与航位推算的比较
- 3.2.1. 非线性系统
- 3.2.2. 高精度估计
- 3.2.3. 适应不确定性
- 3.2.4. 实时性
简述
用Python代码实现EKF的方法对比航位推算的结果,表明EKF的融合定位精度比单纯使用航位推算的精度更高。
1. 背景介绍
1.1. EKF扩展卡尔曼滤波
1.1.1.概念
卡尔曼滤波(Kalman Filtering)是一种用于估计系统状态的递归滤波方法,广泛应用于信号处理、控制系统、机器人技术等领域。扩展卡尔曼滤波(Extended Kalman Filtering)是卡尔曼滤波的一个扩展版本,用于非线性系统的状态估计。
在扩展卡尔曼滤波中,系统被建模为非线性动态系统,其中状态由一个非线性函数描述,并且状态的观测值受到高斯噪声的影响。扩展卡尔曼滤波通过线性化非线性函数来近似系统的动态特性,并利用卡尔曼滤波的递归算法来估计系统的状态。
1.1.2. 扩展卡尔曼滤波的主要步骤如下:
- 初始化:设置系统的初始状态和协方差矩阵。
- 预测:根据系统的动态模型和当前状态的估计值,预测下一个时刻的状态和协方差矩阵。
- 线性化:将非线性函数线性化为一个雅可比矩阵,用于计算卡尔曼增益。
- 更新:根据观测值和预测的状态值,计算卡尔曼增益,并更新状态的估计值和协方差矩阵。
1.1.3. 优、缺点
扩展卡尔曼滤波的优点是能够处理非线性系统,并且具有较好的估计性能。
然而,它对初始状态的估计要求较高,并且线性化过程可能引入估计误差。对于非线性程度较高的系统,线性化可能导致估计误差增大。
因此,在应用扩展卡尔曼滤波时,需要根据实际问题进行参数调整和误差分析,以保证滤波器的性能。
1.2. 航位推算
航位推算(Dead Reckoning)是一种在航海和航空中用于确定当前位置的方法。
其原理基于以下几个假设:
- 起始点位置已知:航位推算需要知道起始点的经纬度坐标。
- 航向角和速度已知:航位推算需要知道航行器的航向角和速度。
- 没有外部干扰:航位推算假设在航行过程中没有外部干扰,如风、水流等。
基于以上假设,航位推算的原理可以描述如下:
1 . 根据起始点位置、航向角和速度,计算出航行器在单位时间内的位移向量
2 . 将位移向量累加到起始点的经纬度坐标上,得到航行器在单位时间后的预测位置。
不断重复步骤1和2,根据航行器的实际航向角和速度更新位移向量,并累加到当前位置上,得到航行器不断更新的位置。
航位推算的原理是基于航行器的运动学原理,通过不断地预测和更新位置,可以在一定程度上确定航行器的当前位置。然而,由于航位推算没有考虑外部干扰和误差累积的问题,所以在长时间航行中可能会产生较大的误差。因此,在实际航行中,航位推算通常会与其他导航方法(如卫星导航系统)结合使用,以提高位置的准确性和可靠性。
1.3. 目前航位算法的使用通常与卡尔曼滤波相结合使用
航位推算导航系统中位置和航向角的发散特性。航位推算导航的可观测性分析表明,所设计的系统能够提供一定时间内的位置和航向角。
但是,需要通过其他系统如绝对定位系统来补偿导航误差,以延长导航时间和距离。本代码将结合扩展卡尔曼滤波实现。
2. 分段代码
2.1. 导入需要的包
import numpy as np
import math
import matplotlib.pyplot as plt
2.2. 设置相关参数
# Estimation parameter of EKF 估计参数
Q = np.diag([0.1, 0.1, np.deg2rad(1.0), 1.0])**2
R = np.diag([1.0, np.deg2rad(40.0)])**2
# Simulation parameter 仿真参数
Qsim = np.diag([0.5, 0.5])**2
Rsim = np.diag([1.0, np.deg2rad(30.0)])**2
DT = 0.1 # time tick [s] 时间刻度
SIM_TIME = 50.0 # simulation time [s] 模拟时间
show_animation = True
2.3. 输入
def calc_input():
v = 1.0 # [m/s]
yawrate = 0.1 # [rad/s] 偏航角速率
u = np.matrix([v, yawrate]).T
return u
2.4. 噪声添加
def observation(xTrue, xd, u):
xTrue = motion_model(xTrue, u)
# add noise to gps x-y 添加噪声到GPS x-y
zx = xTrue[0, 0] + np.random.randn() * Qsim[0, 0]
zy = xTrue[1, 0] + np.random.randn() * Qsim[1, 1]
z = np.matrix([zx, zy])
# add noise to input 给输入加噪
ud1 = u[0, 0] + np.random.randn() * Rsim[0, 0]
ud2 = u[1, 0] + np.random.randn() * Rsim[1, 1]
ud = np.matrix([ud1, ud2]).T
xd = motion_model(xd, ud)
return xTrue, z, xd, ud
2.5. 运动模型
def motion_model(x, u):
F = np.matrix([[1.0, 0, 0, 0],
[0, 1.0, 0, 0],
[0, 0, 1.0, 0],
[0, 0, 0, 0]])
B = np.matrix([[DT * math.cos(x[2, 0]), 0],
[DT * math.sin(x[2, 0]), 0],
[0.0, DT],
[1.0, 0.0]])
x = F * x + B * u
return x
2.6. 观测模型
def observation_model(x):
# Observation Model
H = np.matrix([
[1, 0, 0, 0],
[0, 1, 0, 0]
])
z = H * x
return z
2.7. 雅可比(Jacobian)运动模型
需要注意的是,雅可比运动模型是一种简化的模型,它基于一些假设和近似,可能不能完全准确地描述实际情况。然而,它仍然是解释群体扩散和迁移的有用工具,并且可以通过调整参数和引入更复杂的扩展模型来提高其准确性。
def jacobF(x, u):
"""
Jacobian of Motion Model
motion model
x_{t+1} = x_t+v*dt*cos(yaw)
y_{t+1} = y_t+v*dt*sin(yaw)
yaw_{t+1} = yaw_t+omega*dt
v_{t+1} = v{t}
so
dx/dyaw = -v*dt*sin(yaw)
dx/dv = dt*cos(yaw)
dy/dyaw = v*dt*cos(yaw)
dy/dv = dt*sin(yaw)
"""
yaw = x[2, 0]
v = u[0, 0]
jF = np.matrix([
[1.0, 0.0, -DT * v * math.sin(yaw), DT * math.cos(yaw)],
[0.0, 1.0, DT * v * math.cos(yaw), DT * math.sin(yaw)],
[0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 1.0]])
return jF
def jacobH(x):
# Jacobian of Observation Model 观测模型的雅可比矩阵
jH = np.matrix([
[1, 0, 0, 0],
[0, 1, 0, 0]
])
return jH
2.8. 扩展卡尔曼滤波估计模型
2.8.1. 预测
- 状态预测
系统模型:假设非线性系统的状态方程可以表示为 xPred = f(xEst ,u) + z,其中 x_k 是当前时刻的状态向量,f() 是非线性函数,u是当前时刻的控制输入,z是过程噪声。
预测状态:通过对系统模型进行线性化近似,使用雅可比矩阵(Jacobian Matrix)F_k 来近似表示状态方程:xPred = f̂(xEst, u),其中 xPred是预测的状态估计值,f̂() 是线性化后的状态更新函数。 - 协方差预测
预测协方差:使用雅可比矩阵 jF进行线性化近似,通过更新方程 PPred = jF * PEst * jF.T +Q 来计算预测的协方差矩阵,其中 PPred 是预测的协方差矩阵。
测量模型:假设非线性系统的测量方程可以表示为 zPred = H * xPred其中 z_k 是当前时刻的测量向量,h() 是非线性函数,v_k 是测量噪声。
预测测量:通过对测量模型进行线性化近似,使用雅可比矩阵 jH来近似表示测量方程:zPred = jH * xPred,其中 zPred是预测的测量值,H 是线性化后的测量函数。
残差计算:计算残差向量 y = z.T – zPred 。
残差协方差:假设测量噪声服从高斯分布,通过测量噪声协方差矩阵 R 来描述测量噪声的方差。
估计卡尔曼增益:通过雅可比矩阵 jH 进行线性化近似,计算卡尔曼增益 K = PPred * jH.T * np.linalg.inv(S),其中 S = jH * PPred * jH.T + R 。
更新状态估计值:使用卡尔曼增益将预测的状态估计值修正为最终的状态估计值 xEst = xPrede + K * y。
更新协方差矩阵:使用卡尔曼增益将预测的协方差矩阵修正为最终的协方差矩阵 PEst = (I - K * jH) * Pred ,其中 I 是单位矩阵。
def ekf_estimation(xEst, PEst, z, u):
# Predict
xPred = motion_model(xEst, u)
jF = jacobF(xPred, u)
PPred = jF * PEst * jF.T + Q
# Update
jH = jacobH(xPred)
zPred = observation_model(xPred)
y = z.T - zPred
S = jH * PPred * jH.T + R
K = PPred * jH.T * np.linalg.inv(S)
xEst = xPred + K * y
PEst = (np.eye(len(xEst)) - K * jH) * PPred
return xEst, PEst
2.9. 计算并绘制EKF协方差椭圆
def plot_covariance_ellipse(xEst, PEst): # EKF估计的协方差椭圆
Pxy = PEst[0:2, 0:2]
eigval, eigvec = np.linalg.eig(Pxy)
if eigval[0] >= eigval[1]:
bigind = 0
smallind = 1
else:
bigind = 1
smallind = 0
t = np.arange(0, 2 * math.pi + 0.1, 0.1)
a = math.sqrt(eigval[bigind])
b = math.sqrt(eigval[smallind])
x = [a * math.cos(it) for it in t]
y = [b * math.sin(it) for it in t]
angle = math.atan2(eigvec[bigind, 1], eigvec[bigind, 0])
R = np.matrix([[math.cos(angle), math.sin(angle)],
[-math.sin(angle), math.cos(angle)]])
fx = R * np.matrix([x, y])
px = np.array(fx[0, :] + xEst[0, 0]).flatten()
py = np.array(fx[1, :] + xEst[1, 0]).flatten()
plt.plot(px, py, "--r")
2.10. 主函数
def main():
print(__file__ + " start!!")
time = 0.0
# State Vector [x y yaw v]' 状态向量
xEst = np.matrix(np.zeros((4, 1)))
xTrue = np.matrix(np.zeros((4, 1)))
PEst = np.eye(4)
xDR = np.matrix(np.zeros((4, 1))) # Dead reckoning 船位推算
# history
hxEst = xEst
hxTrue = xTrue
hxDR = xTrue
hz = np.zeros((1, 2))
while SIM_TIME >= time:
time += DT
u = calc_input()
xTrue, z, xDR, ud = observation(xTrue, xDR, u)
xEst, PEst = ekf_estimation(xEst, PEst, z, ud)
# store data history 存储数据历史
hxEst = np.hstack((hxEst, xEst))
hxDR = np.hstack((hxDR, xDR))
hxTrue = np.hstack((hxTrue, xTrue))
hz = np.vstack((hz, z))
if show_animation:
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.sans-serif'] = ['SimHei'] #matplotlib.pyplot绘图显示中文
plt.cla()
plt.plot(hz[:, 0], hz[:, 1], ".g",label="定位观测点") # 绿点为定位观测(如GPS)
plt.plot(np.array(hxTrue[0, :]).flatten(),
np.array(hxTrue[1, :]).flatten(), "-b",
label="真实轨迹") # 蓝线为真实轨迹
plt.plot(np.array(hxDR[0, :]).flatten(),
np.array(hxDR[1, :]).flatten(), "-k",label="航位推算轨迹") # 黑线为航位推算轨迹
plt.plot(np.array(hxEst[0, :]).flatten(),
np.array(hxEst[1, :]).flatten(), "-r",label="EKF估计轨迹") # 红线为EKF估计轨迹
plot_covariance_ellipse(xEst, PEst)
plt.legend()
plt.axis("equal")
plt.grid(True)
plt.pause(0.001)
3. 代码运行结果展示与分析
3.1. 实验结果展示
可以看出一开始航位推算的效果要优于EKF,是因为EKF还处于一个更新调整的阶段,随着时间的推进,航位推算的轨迹与真实的蓝色轨迹相差越来越大,红色的EKF轨迹与真实轨迹之间有误差,但在一定小的一个范围内。图中绿色的点是GPS的观测点,选取一个固定范围内的点来更新预测EKF的轨迹。
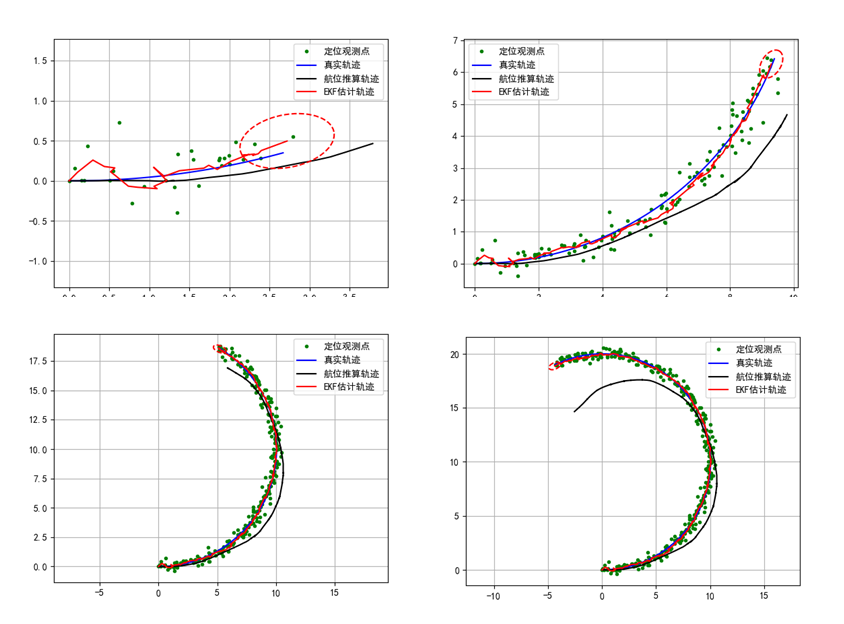
3.2. EKF与航位推算的比较
3.2.1. 非线性系统
船位推算通常涉及到非线性状态方程,如运动模型。
而扩展卡尔曼滤波能够通过对非线性系统进行线性化,使得可以在非线性系统中进行状态估计。
3.2.2. 高精度估计
扩展卡尔曼滤波通过在每个时间步骤上更新状态估计和协方差矩阵,能够提供对船位的高精度估计。通过不断的测量和预测更新过程,可以减小估计误差并产生更准确的船位估计结果。
3.2.3. 适应不确定性
扩展卡尔曼滤波能够处理系统和测量的不确定性。在船位推算中,存在各种误差来源,如传感器误差、环境影响等,扩展卡尔曼滤波能够通过动态调整协方差矩阵来适应这些不确定性,从而提供更鲁棒的航位估计。
3.2.4. 实时性
扩展卡尔曼滤波具有较高的计算效率和实时性,适用于需要实时船位推算的场景。
通过有效的算法设计和优化,扩展卡尔曼滤波能够在短时间内完成状态估计,适用于高频率的航位推算任务。
代码链接:GitHub - UI-Mario/EKF: 扩展卡尔曼滤波/ Extended Kalman Filter(EKF)