目录

介绍： 

代码： 

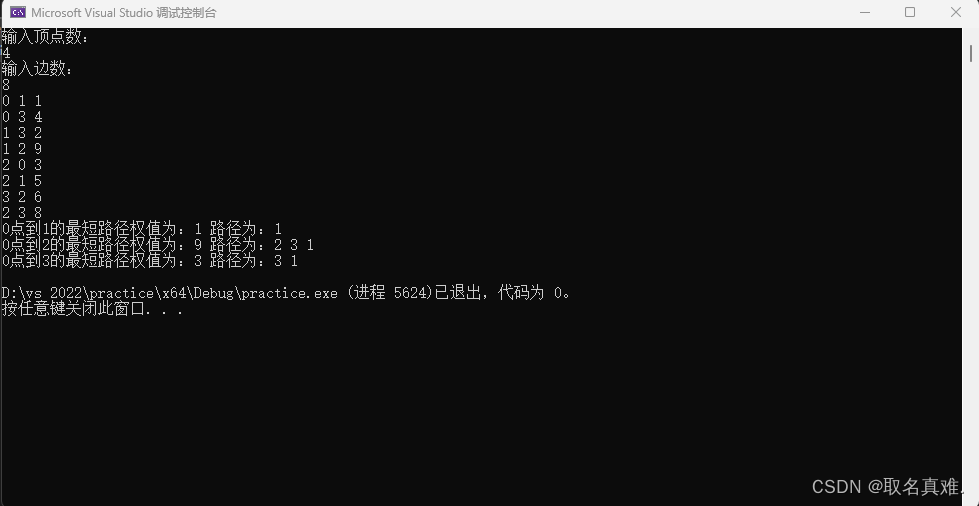
结果： 

介绍： 

弗洛伊德算法（Floyd algorithm）也称为Floyd-Warshall算法，是一种用于求解所有节点对之间的最短路径的动态规划算法。它使用了一个二维数组来存储所有节点之间的最短距离，该数组的初始值为节点之间的直接距离或无穷大。然后，算法对数组进行多次迭代，每次迭代都尝试通过一个中间节点更新节点之间的距离值，直到所有节点之间的最短距离被计算出来。该算法的时间复杂度为O(n^3)，适用于有向图或无向图，但不能处理带有负权边的图。

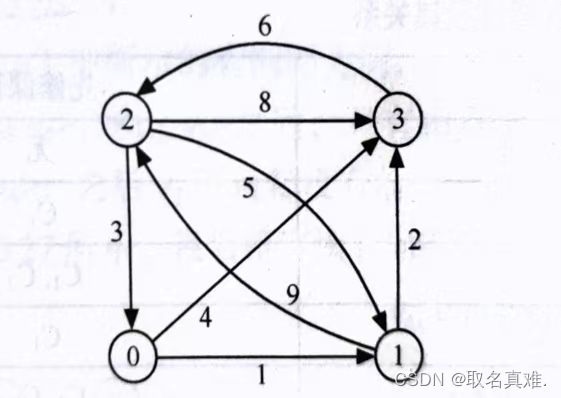
代码： 

#include<iostream>//弗洛伊德算法
using namespace std;
int G[100][100],D[100][100],Path[100][100];
int n, t, maxlen=999;
void Floyd()
{
	for (int i = 0; i < n; i++)//初始化最短路径和前驱
		for(int j=0; j<n; j++)
	    {
			D[i][j] = G[i][j];
			if (D[i][j] < maxlen && i != j)//i和j之间有弧，前驱设为i
				Path[i][j] = i;
			else//i和j之间无弧，前驱设为-1
				Path[i][j] = -1;
	    }
	for(int k=0;k<n;k++)
		for(int i=0;i<n;i++)
			for (int j = 0; j < n; j++)
			{
				if (D[i][k] + D[k][j] < D[i][j])//i到j经过k点有更短路径
				{
					D[i][j] = D[i][k] + D[k][j];//更新D[i][j]
					Path[i][j] = Path[k][j];//更改前驱
				}
			}
	for (int i = 1; i < n; i++)//访问从0点到各点的最短距离
	{
		cout << "0点到" << i << "的最短路径权值为：" << D[0][i] << " ";
		cout << "路径为：";
		int a = Path[0][i];
		cout << i<< " ";
			while (a != 0)
			{
				cout << a << " ";
				a = Path[0][a];
			}
			cout << endl;
	}
}
int main()
{
	cout << "输入顶点数：" << endl;
	cin >> n;
	for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++)
			G[i][j] = maxlen;
	cout << "输入边数：" << endl;
	cin >> t;
	for (int i = 0; i < t; i++)
	{
		int v1, v2, w;
		cin >> v1 >> v2 >> w;
		G[v1][v2] = w;
	}
	Floyd();
}

结果：