前置知识

有序集合中的每个元素都有⼀个唯⼀的浮点类型的分数（score）与之关联，这使得有序集合中的元素是可以维护有序性的，进行排序的时候，就是按照此处的分数大小进行升序/降序排序

注意：zset主要还是用来存member，score只是辅助

例子：使用有序集合显⽰三国中的武将的武⼒

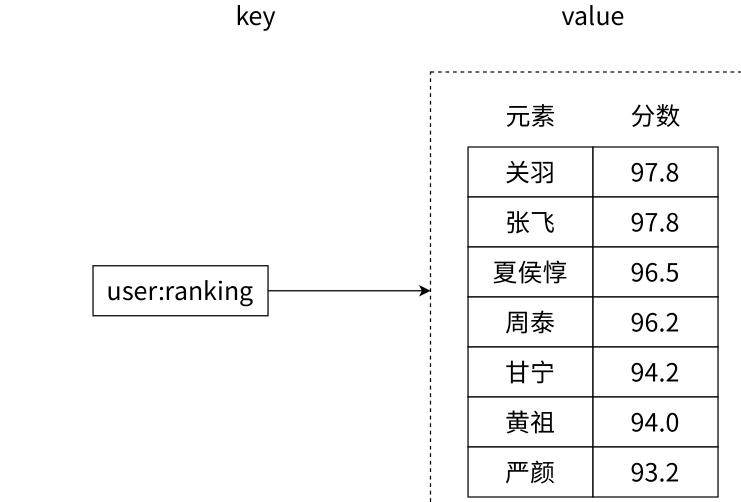
• 分数不同，则按照分数来升序排序（zset内部按照升序排列），分数相同的时候，再按照元素自身字符串的字典序来排序

有序集合中的元素是不能重复的，但分数允许重复。类⽐于⼀次考试之后，每个⼈⼀定有⼀个唯⼀的分数，但分数允许相同

---

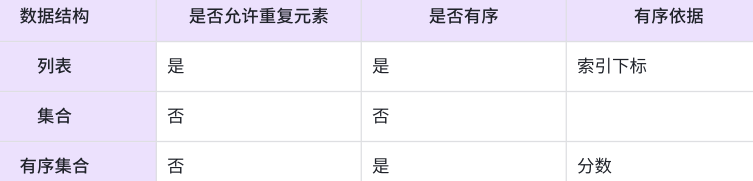
列表、集合、有序集合三者的异同点

---

普通命令

ZADD

添加或者更新指定的元素以及关联的分数到zset中，分数应该符合double类型，+inf/-inf作为正负极限也是合法的

语法：ZADD key [NX | XX] [GT | LT] [CH] [INCR] score member [score member...]

相关选项：

• XX：仅仅⽤于更新已经存在的元素，不会添加新元素
• NX：仅⽤于添加新元素，不会更新已经存在的元素
• CH：默认情况下，ZADD返回的是本次添加的元素个数，但指定这个选项之后，就会还包含本次更新的元素的个数，可能会影响zadd的返回值
  • 注意:通常ZADD的返回值只计算添加的新元素的数量。
• INCR：此时命令类似ZINCRBY的效果，将元素的分数加上指定的分数。此时只能指定⼀个元素和分数

返回值：本次添加成功的元素个数 时间复杂度：O(log(N))

• 注意：之前hash，set，list添加一个元素都是$O(1)$，但是zset添加元素的时间复杂度为$O(logN)$，这是因为zset是有序结构，要新增新元素，要放到合适的位置上，之所以不是$O(N)$，是因为zset内部的数据结构为调表

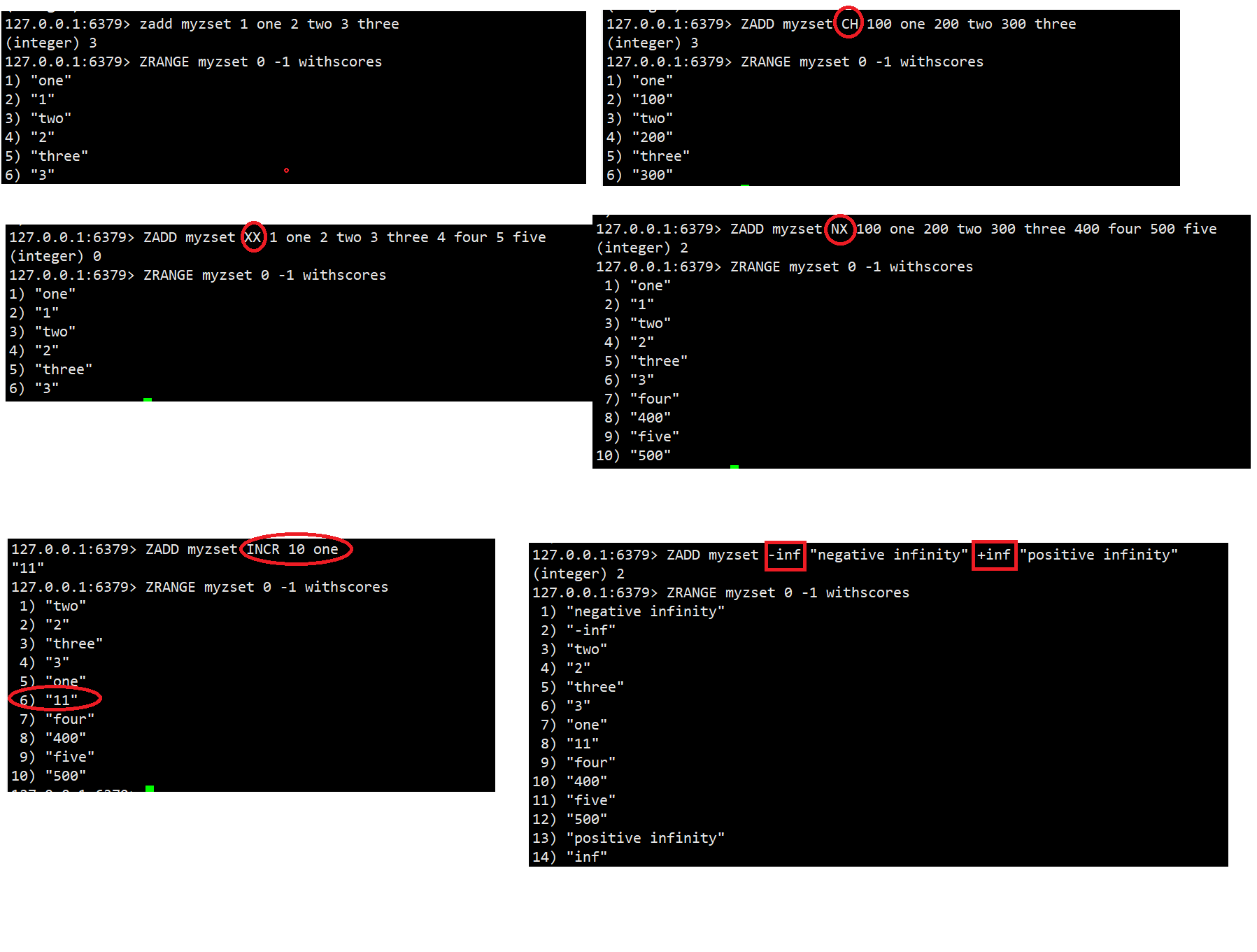
不加NX || XX选项的时候：

• 如果当前member不存在，此时就会达到添加新member的效果
• 如果当前member已经存在，此时就会更新分数

XX:只更新已经存在的元素。不要添加新元素。

NX:只添加新元素。不要更新已经存在的元素。

---

LT和ET：

LT：现在要更新分数了，发现现在给定的新的分数比之前的分数小，此时就更新成功，否则就不更新

• 只有当新分数小于当前分数时才会更新现有元素。这个标志不会阻止添加新元素

GT:仅在新分数大于当前分数时更新现有元素。这个标志不会阻止添加新元素。

---

ZCARD

获取⼀个zset的基数（cardinality），即zset中的元素个数

语法：ZCARD key

返回值：zset内的元素个数 时间复杂度：O(1)

ZCOUNT

返回分数在min和max之间的元素个数，默认情况下，min和max都是包含的，即范围是$[min，max]$，可以通过(来排除边界值

语法：ZCOUNT key min max

返回值：满⾜条件的元素列表个数 时间复杂度：O(log(N))

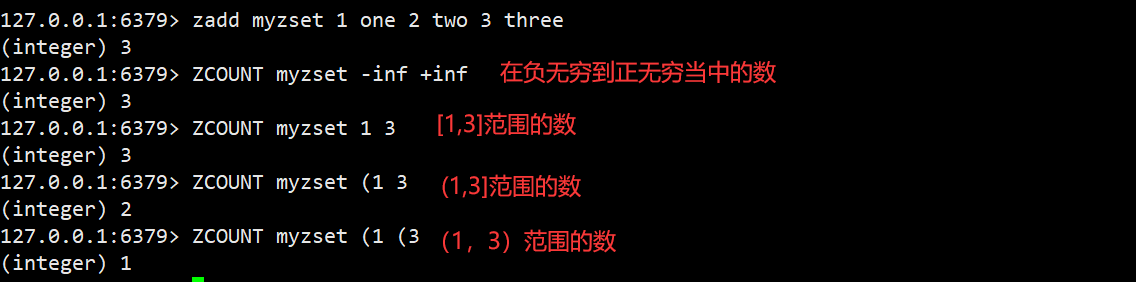
时间复杂度分析：先根据min找到对应的元素，再根据max找到对应的元素（时间复杂度为：$O(logN)$），实际上，zset内部会记录每个元素当前的排行/次序，查询到元素就直接知道了元素所在的次序（下标），就可以直接把max对应的元素的次序和min对应的元素的次序做减法即可

注意1：min和max可以写成浮点数，因为zset的分数本身就是浮点数

注意2：在浮点数当中，存在两个特殊的数值：inf表示无穷大，-inf表示负无穷大（负无穷大 != 无穷小）

---

ZRANGE

返回指定区间⾥的元素，分数按照升序。带上WITHSCORES可以把分数也返回

语法：ZRANGE key start stop [WITHSCORES] 

• 注意：此处的[start，stop]为下标构成的区间.从0开始，⽀持负数.

返回值：区间内的元素列表 时间复杂度：O(log(N)+M)

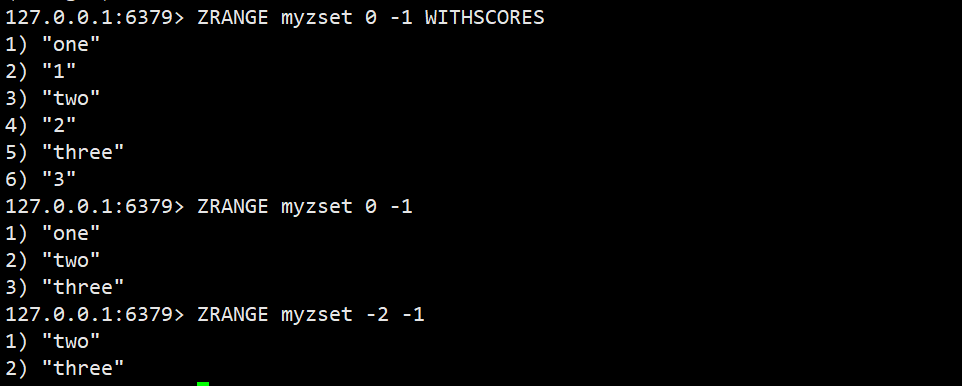
时间复杂度分析：先根据下标找到边界值（O(logN)），然后从start对应位置开始往后遍历，M:start-stop区间的元素个数

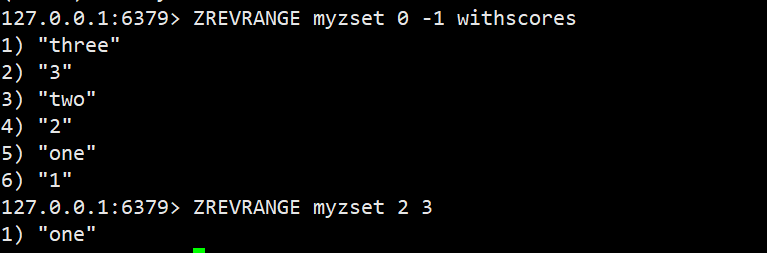
ZREVRANGE

返回指定区间⾥的元素，按照分数降序打印，带上WITHSCORES可以把分数也返回

语法：ZREVRANGE key start stop [WITHSCORES]

返回值：区间内的元素列表 时间复杂度：O(log(N)+M)

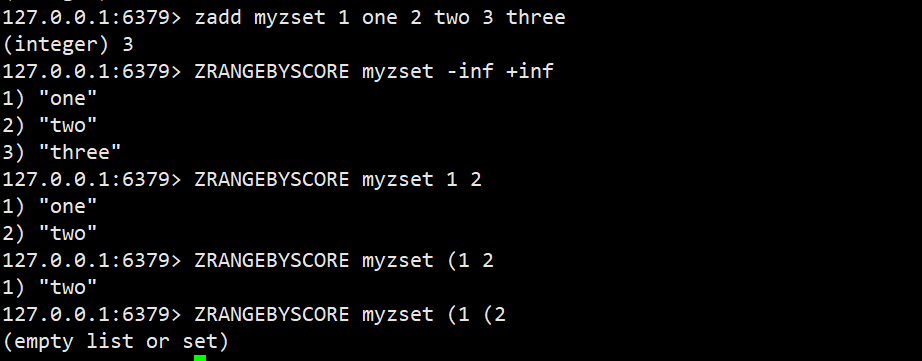
ZRANGEBYSCORE

返回分数在min和max之间的元素，默认情况下，min和max都是包含的，可以通过(排除

语法：ZRANGEBYSCORE key min max [WITHSCORES] 

返回值：区间内的元素列表 时间复杂度：O(log(N)+M)

ZPOPMAX

删除并返回分数最⾼的count个元素

语法：ZPOPMAX key [count] 

返回值：分数和元素列表 时间复杂度：*O(log(N)M)

• N：有序集合元素个数 M：count要删除的元素个数

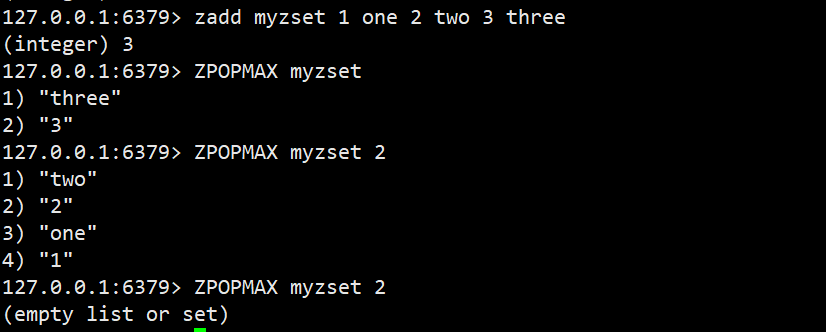
如果存在多个元素分数相同，同时为最大值的时候，zpopmax进行删除，如果不指定count，仍然只删除其中一个元素

• 如果分数相同会按照member字符串的字典序排序

---

注意：此处删除的是最大值，在有序集合当中，最大值相当于就是最后一个元素（删除最大值==>尾删），既然是尾删，此时可以把最后一个元素的位置特殊记录下来，后续就可以以$O(1)$的复杂度进行删除，所以$O(logN)=>O(1)$是可能的，但是redis并没有这么做

---

BZPOPMAX

ZPOPMAX的阻塞版本，有序集合可以视为是优先级队列，此时使用bzpopmax就相当于是一个带有阻塞功能的优先级队列

语法：BZPOPMAX key [key ...] timeout #timeout：超时时间,单位是s，支持小数形式，写做0.1 就是代表100ms

返回值：元素列表 时间复杂度：O(log(N)) =>删除最大值花费的时间

可以同时等待多个key对应的有序集合当中的元素就绪，阻塞到有其它客户端往任意一个key当中插入元素。如果有序集合已经有元素了，直接就能返回，不会阻塞

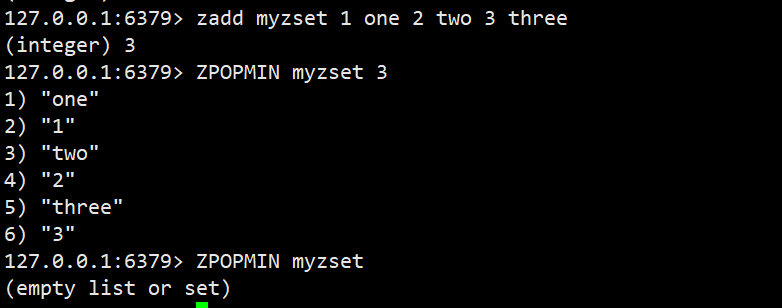
ZPOPMIN

删除并返回有序集合当中分数最低的count个元素

语法：ZPOPMIN key [count] 

返回值：分数和元素列表 时间复杂度：O(log(N)*M)

BZPOPMIN

ZPOPMIN的阻塞版本

语法：BZPOPMIN key [key ...] timeout 

返回值：元素列表 时间复杂度：O(log(N))

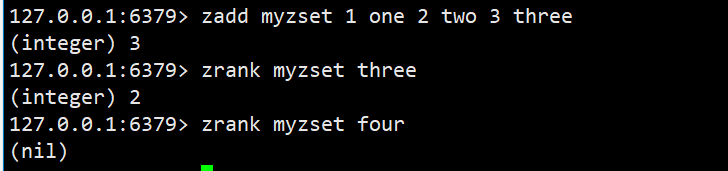
ZRANK

返回指定元素的排名，升序计算下标

语法：ZRANK key member 

返回值：排名 时间复杂度：O(log(N)) =>查询位置的过程

注意：zcount在计算的时候，就是先根据分数找到元素，再根据元素获取到排名，再把排名相减就得到了元素个数

zrank得到的下标，是从前往后计算的，下标从0开始

ZREVRANK

返回指定元素的排名，降序计算下标（是从后往前计算的，下标从0开始）

语法：ZREVRANK key member 

返回值：排名 时间复杂度：O(log(N))

---

ZSCORE

返回指定元素的分数

语法：ZSCORE key member 

返回值：分数 时间复杂度：O(1)

注意：前面根据member找分数都是$logN$，此处相当于是redis对于这样的查询做了优化，付出了额外的空间代价，优化到了$O(1)$查询

ZREM

删除指定的元素

语法：ZREM key member [member ...] 

返回值：本次操作删除的元素个数 时间复杂度：O(M*log(N))

• N：有序集合元素个数 M：参数当中member的个数

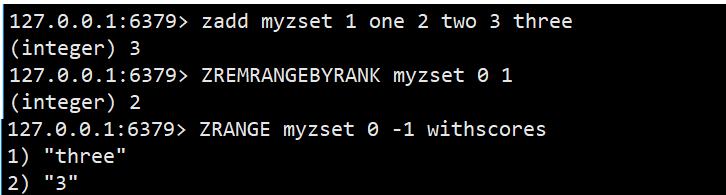
ZREMRANGEBYRANK

按照排序，升序删除指定范围的元素，左闭右闭$[start,stop]$

语法：ZREMRANGEBYRANK key start stop 

返回值：本次操作删除的元素个数 时间复杂度：O(log(N)+M)

• N：有序集合元素个数 M：$stop-start$区间的元素个数

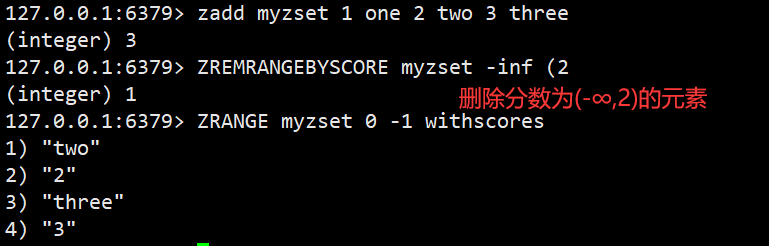
ZREMRANGEBYSCORE

按照分数删除指定范围的元素，左闭右闭$[min,ma]$，可以通过(排除边界值

语法：ZREMRANGEBYSCORE key min max 

返回值：本次操作删除的元素个数 时间复杂度：O(log(N)+M)

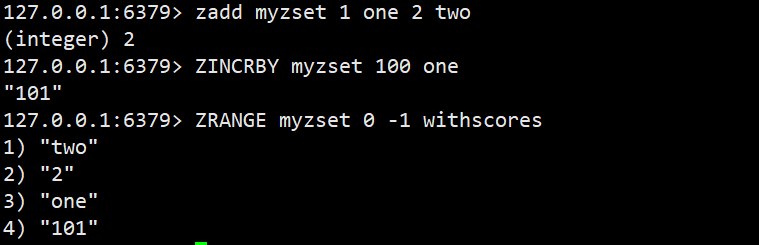
ZINCRBY

为指定的元素的关联分数添加指定的分数值，修改之后，仍然会保持整个有序集合是升序的

语法：ZINCRBY key increment member 

返回值：增加后元素的分数 时间复杂度：O(log(N))

---

集合之间的操作

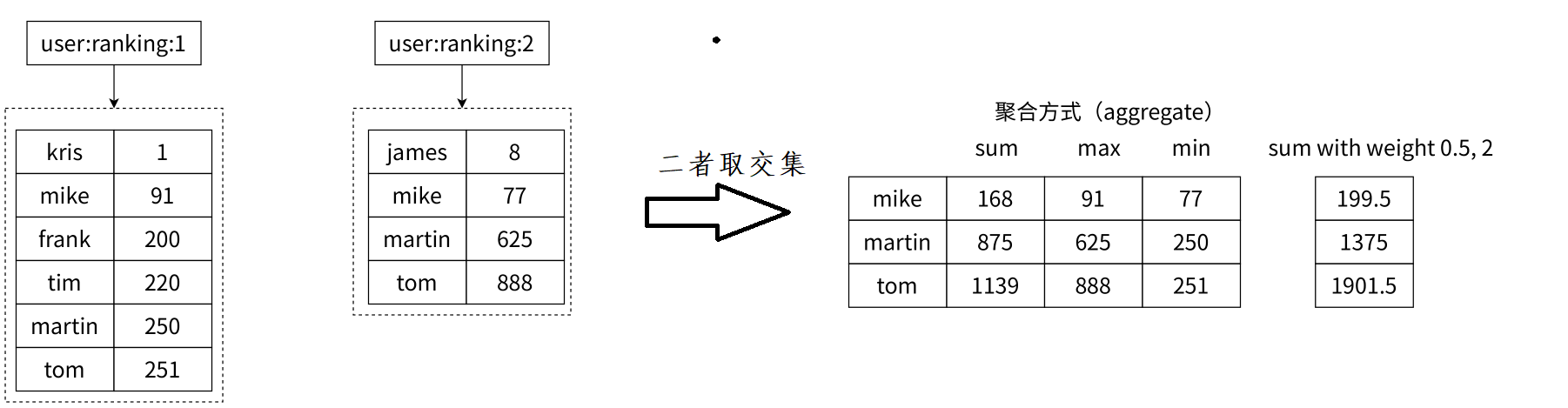
ZINTERSTORE

出给定有序集合中元素的交集并保存进⽬标有序集合中，在合并过程中以元素为单位进⾏合并，元素对应的分数按照不同的聚合⽅式和权重得到新的分数

语法：ZINTERSTORE destination numkeys key [key ...] [WEIGHTS weight  [weight ...]] [AGGREGATE <SUM | MIN | MAX>]

• destination：要把求得的交集存储到哪个key当中，对应的zset
• numkeys：是一个整数，描述后续有几个key参与交集运算
• weights：权重，因为是有序集合，带有分数，此处的权重相当于是一个系数，会乘当前的分数
• AGGREGATE：表示最后交集的结果取什么结果，求和，最小值，最大值

有序集合的交集操作

返回值：⽬标集合中的元素个数

时间复杂度：O(N*K)+O(M*log(M))

• N是输⼊的有序集合中，最⼩的有序集合的元素个数
• K是输⼊了⼏个有序集合 ==>多少个有序集合进行合并求交集
• M是最终结果的有序集合的元素个数

K一般不会很多，可以近似看成1，也可以认为N和M是接近的（同一个数量级），那么O(N*K)+O(M*log(M)) =>O(M) + O(M * logM) =>O(M*logM)

---

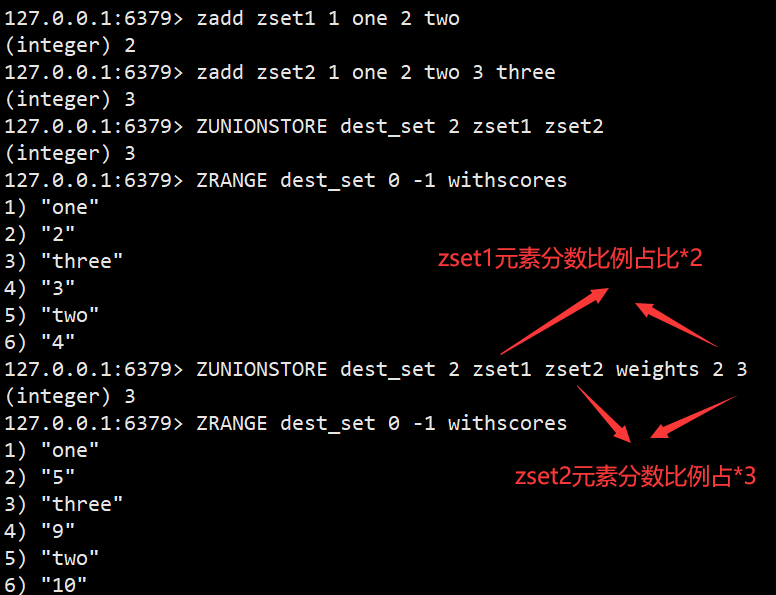
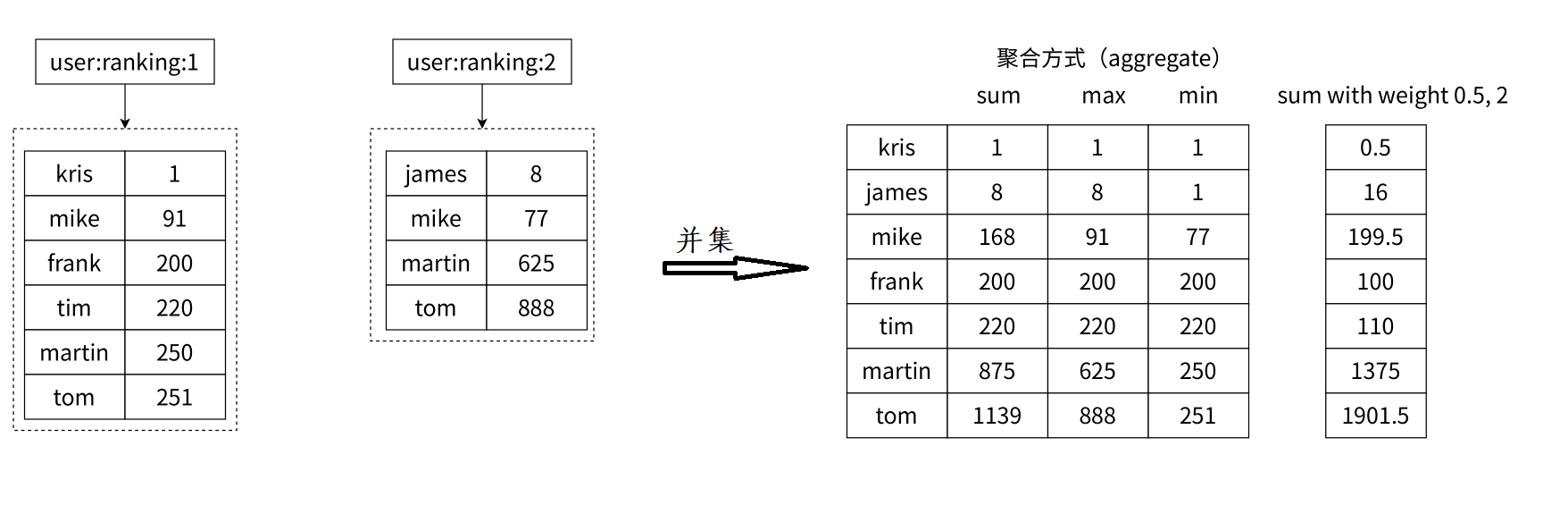
ZUNIONSTORE

求出给定有序集合中元素的并集并保存进⽬标有序集合中，在合并过程中以元素为单位进⾏合并，元素对应的分数按照不同的聚合⽅式和权重得到新的分数

语法：ZUNIONSTORE destination numkeys key [key ...] [WEIGHTS weight  [weight ...]] [AGGREGATE <SUM | MIN | MAX>]

有序集合的并集操作

---

返回值：⽬标集合中的元素个数

时间复杂度：O(N)+O(M*log(M))N是输⼊的有序集合总的元素个数;M是最终结果的有序集合的元素个数

---

命令小结

---

内部编码

有序集合类型的内部编码有两种：

• ziplist（压缩列表）：当有序集合的元素个数⼩于zset-max-ziplist-entries配置（默认128个），同时每个元素的值都⼩于zset-max-ziplist-value配置（默认64字节）时，Redis会⽤ziplist来作为有序集合的内部实现，ziplist可以有效减少内存的使⽤
• skiplist（跳表）：当ziplist条件不满⾜时（元素个数比较多或者单个元素比较大），有序集合会使⽤skiplist作为内部实现，因为此时ziplist的操作效率会下降
  • 跳表是一个复杂链表，查询元素的时间复杂度为$logN$，相比于树形结构，更适合按照范围获取元素

---

测试内部编码

1）当元素个数较少且每个元素较⼩时，内部编码为ziplist

2）当元素个数超过128个，内部编码skiplist

3）当某个元素⼤于64字节时，内部编码skiplist

---

使用场景

有序集合⽐较典型的使⽤场景就是排⾏榜系统。例如常⻅的⽹站上的热榜信息，榜单的维度可能是多⽅⾯的：按照时间、按照阅读量、按照点赞量。

例子：使⽤点赞数这个维度，维护每天的热榜：

1）添加⽤⼾赞数：例如⽤⼾james发布了⼀篇⽂章，并获得3个赞，可以使⽤有序集合的zadd和zincrby功能

zadd user:ranking:2022-03-15 3 james 

之后如果再获得赞，可以使⽤zincrby：

zincrby user:ranking:2022-03-15 1 james 

2）取消⽤⼾赞数：由于各种原因（例如⽤⼾注销、⽤⼾作弊等）需要将⽤⼾删除，此时需要将⽤⼾从榜单中删除掉，可以使⽤zrem。例如删除成员tom

zrem user:ranking:2022-03-15 tom 

3）展⽰获取赞数最多的10个⽤⼾

zrevrangebyrank user:ranking:2022-03-15 0 9

4）展⽰⽤⼾信息以及⽤⼾分数

该功能将⽤⼾名作为键后缀，将⽤⼾信息保存在哈希类型中，⾄于⽤⼾的分数和排名可以使⽤zscore和zrank来实现

hgetall user:info:tom
zscore user:ranking:2022-03-15 mike
zrank user:ranking:2022-03-15 mik