#Apollo开发者#
学习课程的传送门如下,当您也准备学习自动驾驶时,可以和我一同前往:
《自动驾驶新人之旅》免费课程—> 传送门
《Apollo Beta宣讲和线下沙龙》免费报名—>传送门
文章目录
前言
控制器设计
比例积分微分控制
线性二次调节器
模型预测控制
Tips
总结
前言
见《自动驾驶学习笔记(一)——Apollo平台》
见《自动驾驶学习笔记(二)——Apollo入门》
见《自动驾驶学习笔记(三)——场景设计》
见《自动驾驶学习笔记(四)——变道绕行仿真》
见《自动驾驶学习笔记(五)——绕行距离调试》
见《自动驾驶学习笔记(六)——Apollo安装》
见《自动驾驶学习笔记(七)——感知融合》
见《自动驾驶学习笔记(八)——路线规划》
控制器设计
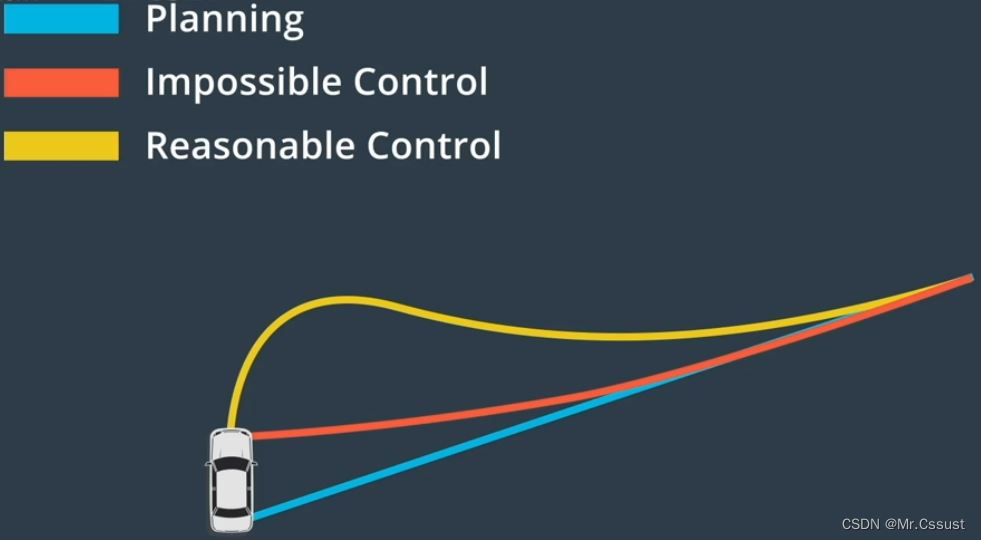
控制器设计目标:使车辆行驶的轨迹尽可能贴近Planning层规划的轨迹,如下图所示:

控制器的输入信息:Planning层计算出来的行驶路线,由一系列轨迹点组成,如下图所示:
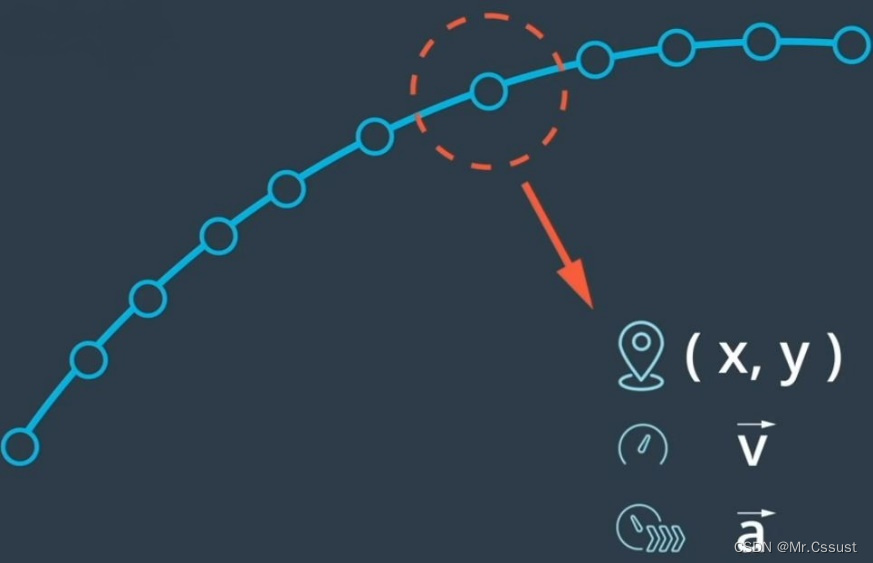
控制的执行器:加速、制动、转向,如下图所示:

可行性约束:所有物理量的值不能突变,如下图所示:
平稳度约束:速度尽可能稳定,方向尽可能稳定,如下图所示:
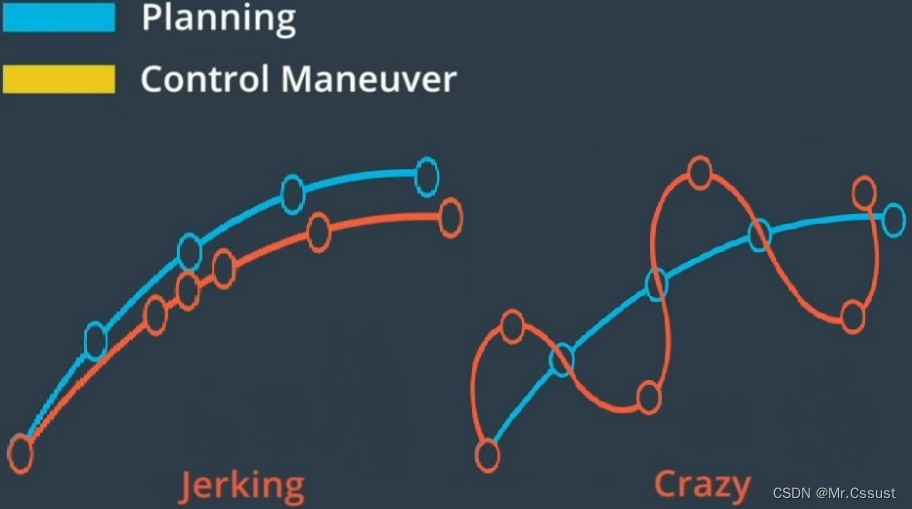
实现上述控制器设计,常见的算法有三种:PID、LQR、MPC。
比例积分微分控制
PID(Proportional Integral Derivative Control),比例积分微分控制,这种算法比较常见,也很典型,本文不做过多介绍。
线性二次调节器
LQR(Linear Quadratic Regulator),线性二次调节器其中的L是指被控对象的状态与控制变量之间是线性关系,Q是指在求解最优参数时为保证绝对值之和最小引入了一个2次方。本文以车辆的横向控制为例介绍LQR的基本思路。
如下图所示,车辆的状态向量x包括:横向偏移量cte、cte变化率、朝向交偏移量θ、θ变化率,控制车辆的执行器包括:转型、加速、制动。x和u之间是线性的关系。
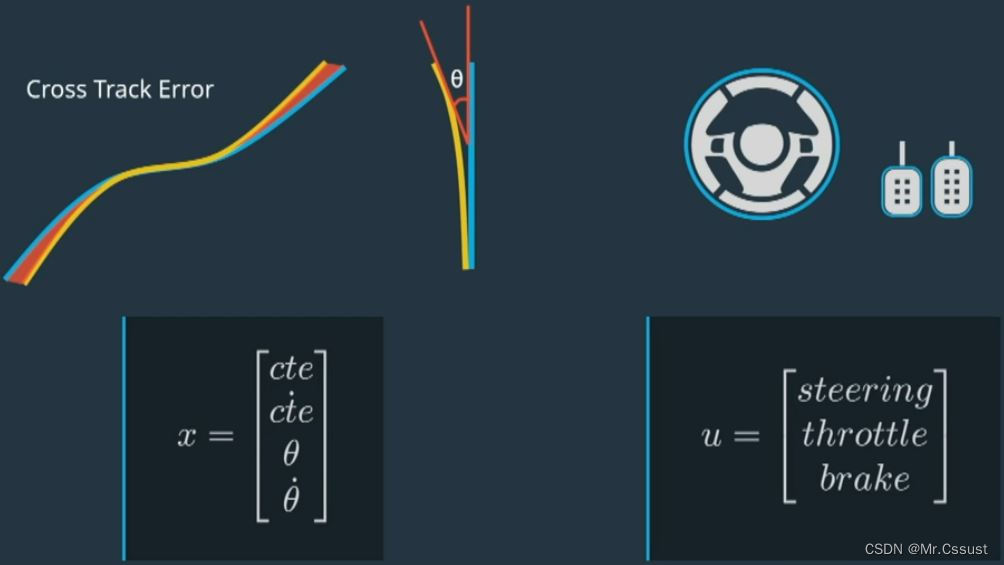
控制器设计目标是让x逼近零,实现这个目标的同时也要求投入尽可能少的成本,即u的变化量可能小,所以这里引入控制成本函数如下公式,其中的Q和R是一对权重比例系数。

因为x中有正有负,为了在cost求极值时方便一些,引入了他们的2次方,并设置了向量各个部分的权重比例系数,如下公式:
![]()
对cost函数求极值,当cost最小时,得到u和x之间的关系式如下:
![]()
这里K即要设计的控制器,是一个很复杂的函数。
模型预测控制
MPC(Model Predictive Control),模型预测控制的不步骤如下:
1)建立车辆模型;
2)监测当前的车辆状态;
3)通过该模型计算,车辆从当前状态进入下一个目标状态,需要输出的u;
4)车辆执行这个u;
5)监测新的车辆状态,重复2)到4)的步骤,过程期间适时优化1)中的车辆模型
Tips
PID通常用于纵向的速度控制
LQR通常用于横向的方向控制
MPC通常只用于学术研究
总结
以上就是本人在学习自动驾驶时,对所学课程的一些梳理和总结。后续还会分享另更多自动驾驶相关知识,欢迎评论区留言、点赞、收藏和关注,这些鼓励和支持都将成文本人持续分享的动力。
另外,如果有同在小伙伴,也正在学习或打算学习自动驾驶时,可以和我一同抱团学习,交流技术。
版权声明,原创文章,转载和引用请注明出处和链接,侵权必究!
文中部分图片来源自网络,若有侵权,联系立删。






![[C/C++] 数据结构 LeetCode:用队列实现栈](https://img-blog.csdnimg.cn/80fe4cf53fa4475d8c75f7a3725877b8.png)