文章目录
- 上一篇
- 动态规划性质
- 矩阵连乘问题
- 凸多边形最优三角部分
- 最长公共子序列
- 0-1背包问题
- 下一篇
上一篇
算法设计与分析复习–递归与分治(二)
动态规划性质
与分析法类似:将原问题分解为子问题
不同点:不是通过递归的方式,而是自底向上的求解问题

矩阵连乘问题

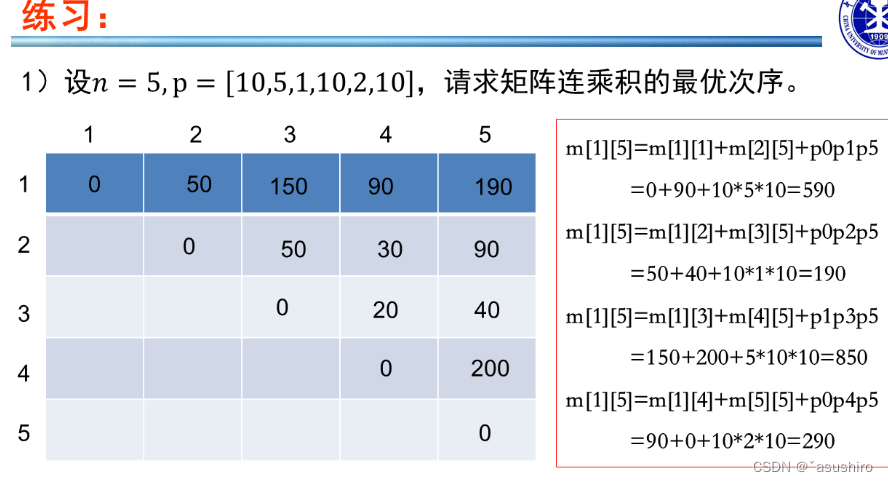
矩阵连乘的次数是左矩阵行列,右矩阵行列取出左右中进行相乘。

由于矩阵乘积需要满足左矩阵列等于右矩阵的行,所以可以用一维数组进行存n个矩阵,共n + 1个元素,从第一个矩阵的(1)行(2)列,第二个矩阵由于行与第一个的列相同就不在重复存储所以只需存第二个的(3)列,一次类推
数据结构:
a[N] 存矩阵行列
dp[N][N] => dp[i][j]表示第i个矩阵到第j个矩阵的最小连乘次数
因为是从小到大算每个区间内的最小值=> 区间dp

#include <iostream>
#include <cstring>
#include <algorithm>
#include <climits>
using namespace std;
const int N = 110;
int a[N], dp[N][N], n;
void out()
{
for (int i = 1; i <= n; i ++)
{
for (int j = 1; j <= n; j ++)
printf("%d ", dp[i][j]);
puts("");
}
}
int main()
{
scanf("%d", &n);
for (int i = 0; i <= n; i++) scanf("%d", &a[i]);
// 初始化dp数组
memset(dp, 0, sizeof(dp));
for(int len = 2; len <= n; len ++)
{
for (int i = 1; i + len - 1 <= n; i ++)
{
int j = i + len - 1;
dp[i][j] = 1e8; // 初始化为一个较大的值
for (int k = i; k < j; k ++)
{
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + a[i - 1] * a[k] * a[j]);
// out();
}
}
}
out();
printf("%d\n", dp[1][n]);
return 0;
}



区间DP类似题目 AcWing.282石子合并
凸多边形最优三角部分
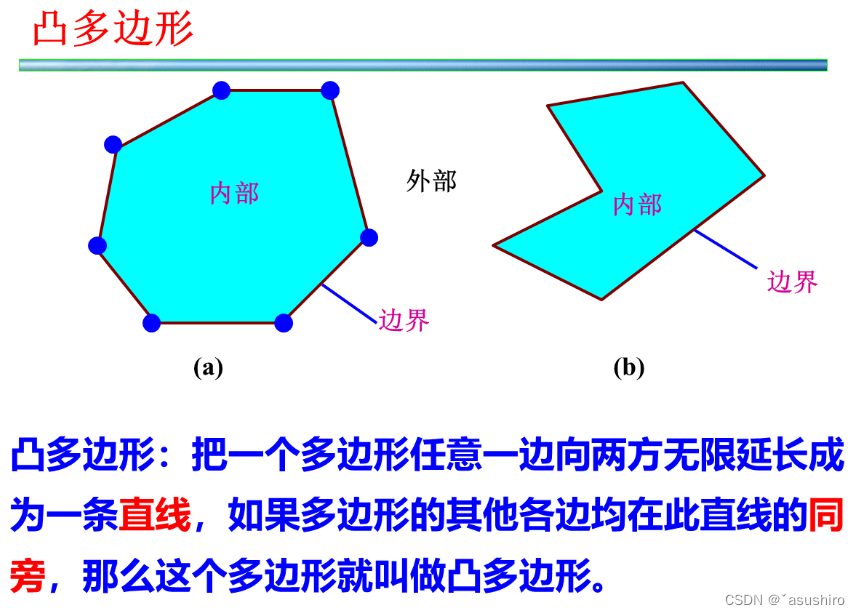
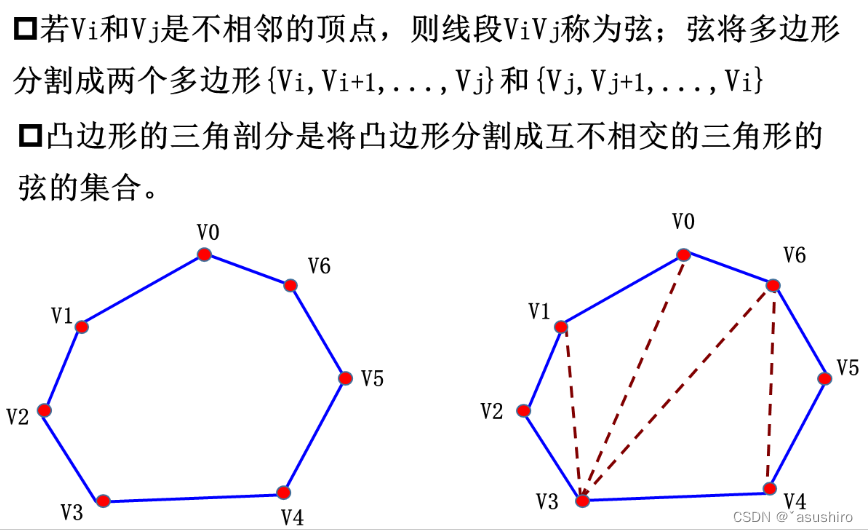
问题描述

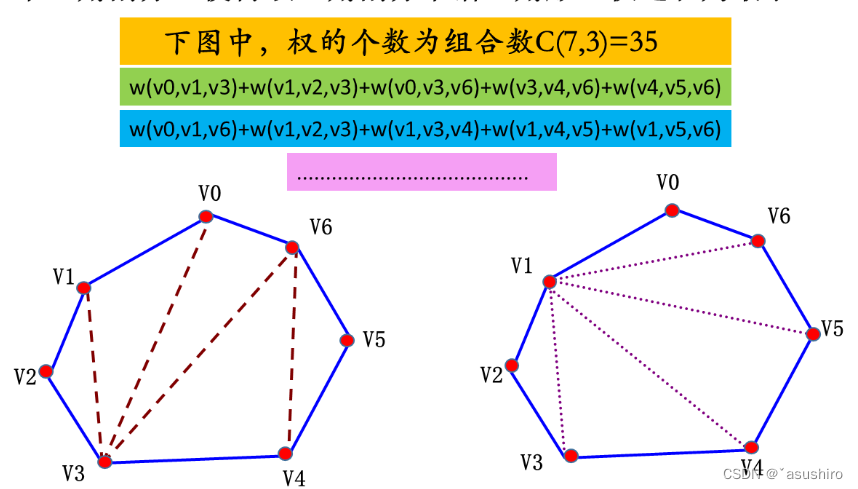
可以转换成矩阵连乘问题
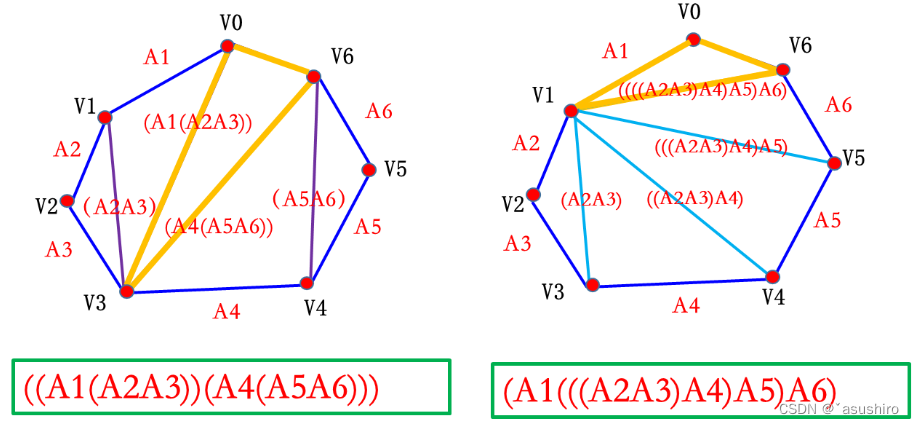
加完括号的形式就是那个最优三角形的位置
数据结构
v[N]: 表示每个结点对应值
dp[N][N]: dp[i][j]表示结点从 i 到 j 的三角的权重,取min
状态计算(区间dp):
d
p
[
i
]
[
j
]
=
m
i
n
{
d
p
[
i
]
[
k
]
+
d
p
[
k
+
1
]
+
w
(
v
i
−
1
v
k
v
j
)
}
dp[i][j] = min\{ dp[i][k] + dp[k + 1] + w(v_{i-1}v_kv_j)\}
dp[i][j]=min{dp[i][k]+dp[k+1]+w(vi−1vkvj)}

最长公共子序列

AcWing897.最长公共子序列

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 1010;
char a[N], b[N];
int dp[N][N], n, m;
int x[N][N];//寻路数组
vector<char> ans;
void out()
{
for (int i = 1; i <= n; i ++)
{
for (int j = 1; j <= m; j ++)
cout << dp[i][j] << ' ';
cout << endl;
}
cout << "*****************" << endl;
for (int i = 1; i <= n; i ++)
{
for (int j = 1; j <= m; j ++)
cout << x[i][j] << ' ';
cout << endl;
}
cout << "*****************" << endl;
}
void trackback(int i, int j)
{
if (i <= 0 || j <= 0) return;
if (x[i][j] == 1){
ans.push_back(a[i]);
trackback(i - 1, j - 1);
}
else if (x[i][j] == 2) trackback(i - 1, j);
else trackback(i, j - 1);
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
cin >> a + 1 >> b + 1;//因为有i - 1操作所以起始下标要从1开始防止数组越界
for(int i = 1; i <= n; i ++)
{
for (int j = 1; j <= m; j ++)
{
if(a[i] == b[j]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
x[i][j] = 1;// 1表示i和j都要选为对应公共元素
}
else if(dp[i - 1][j] >= dp[i][j - 1]){
dp[i][j] = dp[i - 1][j];
x[i][j] = 2;//回溯沿着表上走
}
else{
dp[i][j] = dp[i][j - 1];
x[i][j] = 3;//沿着表左走
}
}
}
out();
cout << dp[n][m] << endl;
trackback(n, m);
reverse(ans.begin(), ans.end());//答案顺序反了,需要翻转一下
for (auto i : ans)
cout << i;
return 0;
}
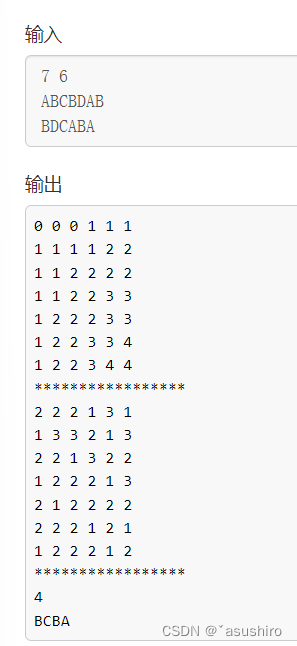

输入顺序写反了,列是第一个序列,行时第二个序列



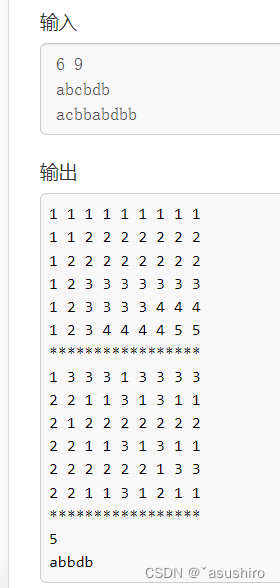
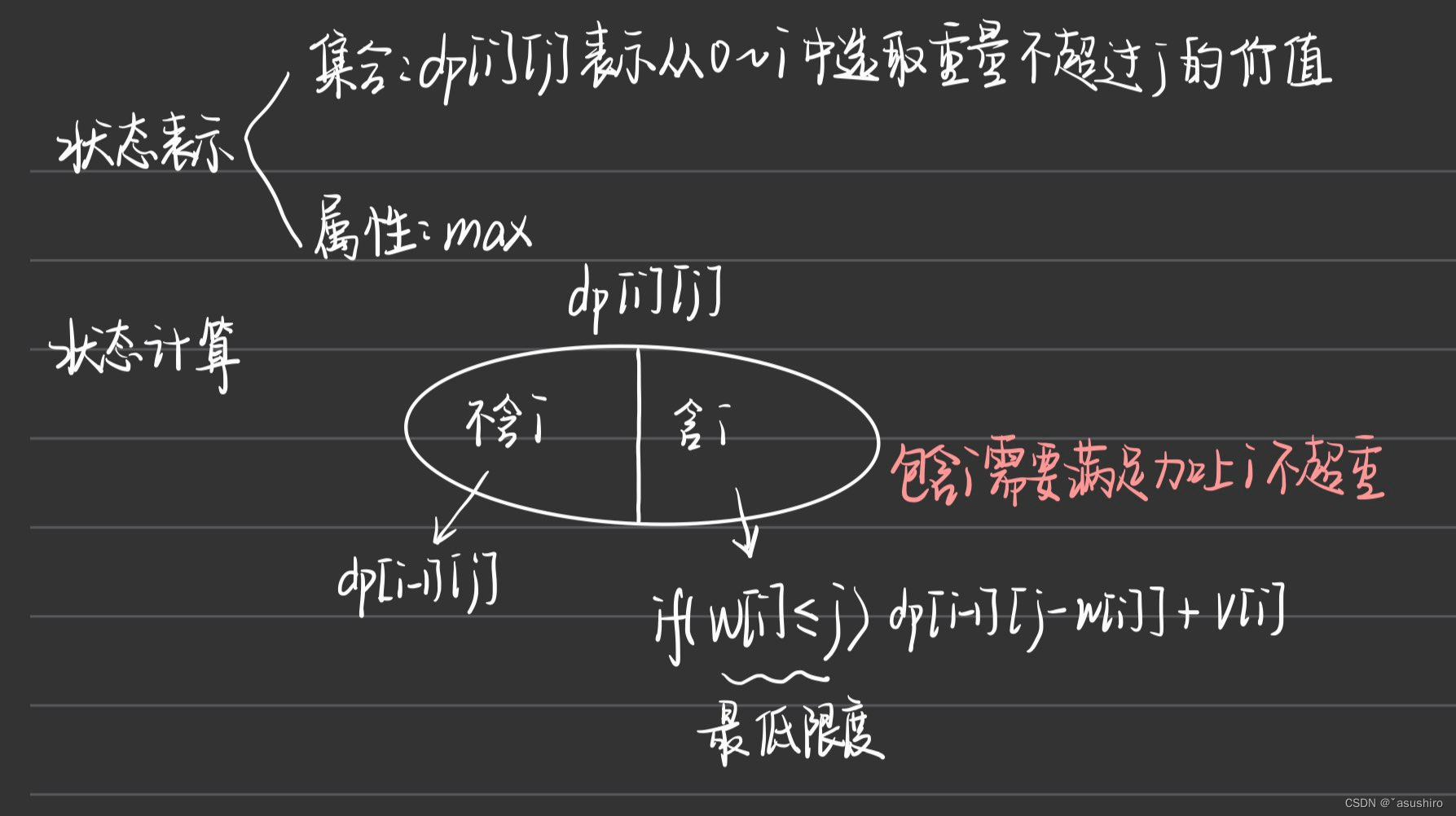
0-1背包问题
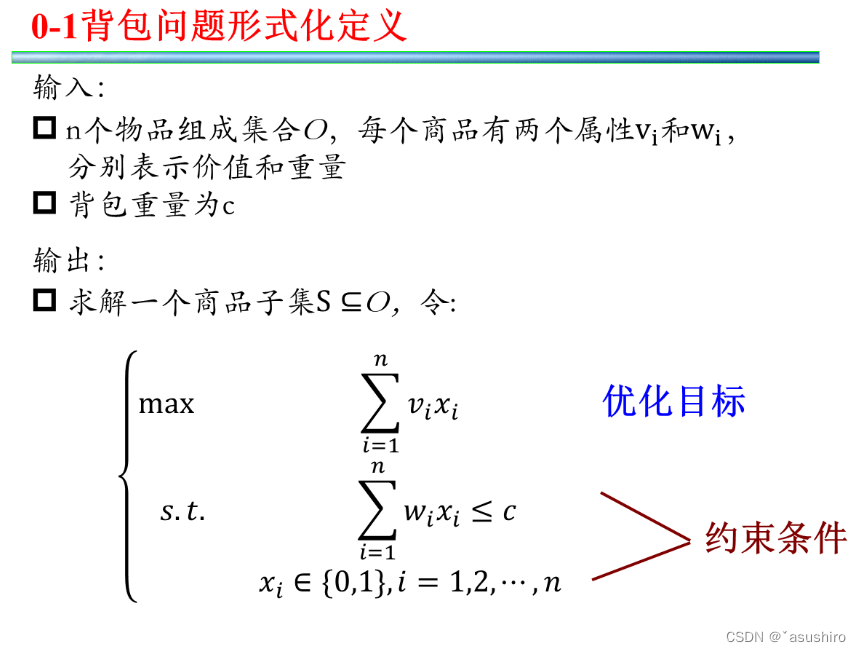
AcWing2. 01背包
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int dp[N][N], w[N], v[N], n, c;
int main()
{
scanf("%d%d", &n, &c);
for (int i = 1; i <= n; i ++) scanf("%d%d", &w[i], &v[i]);
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= c; j ++)
{
dp[i][j] = dp[i - 1][j];
if(w[i] <= j) dp[i][j] = max(dp[i][j], dp[i - 1][j - w[i]] + v[i]);
}
printf("%d", dp[n][c]);
return 0;
}
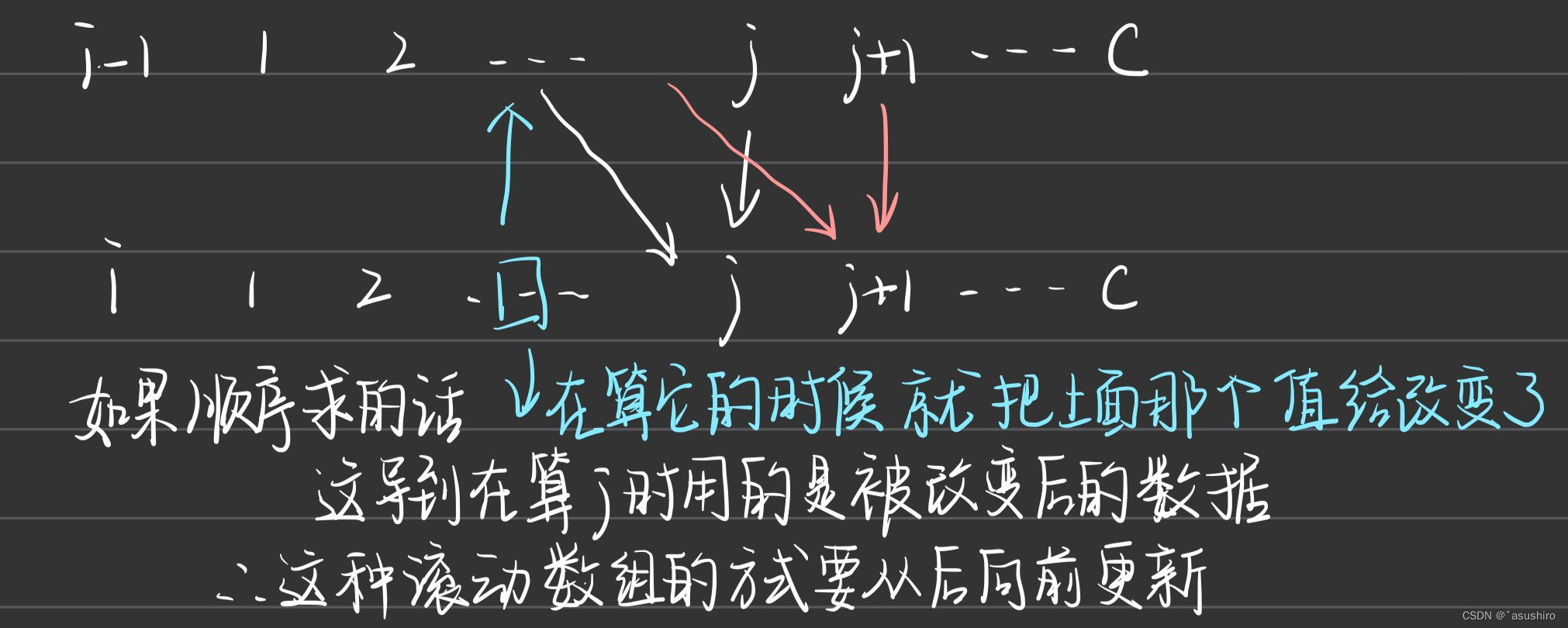
观察发现状态计算的方程中只用到了第i行和第i - 1行,所以可以用滚动数组,将这个二维数组优化成一维数组
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int dp[N], w[N], v[N], n, c;
int main()
{
scanf("%d%d", &n, &c);
for (int i = 1; i <= n; i ++) scanf("%d%d", &w[i], &v[i]);
for (int i = 1; i <= n; i ++)
for (int j = c; j >= 1; j --)// 也可以将下面if条件拿到上面=> for(int j = c; j >= w[i]; j --)
{
if(w[i] <= j) dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
}
printf("%d", dp[c]);
return 0;
}
带结果回溯的写法
如果用回滚数组就找不到对应物品的坐标了,但是可以找到对应价值的物品
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int dp[N][N], w[N], v[N], n, c;
int x[N][N];
void out()
{
for (int i = 1; i <= n; i ++)
{
for (int j = 1; j <= c; j ++)
printf("%d ", dp[i][j]);
puts("");
}
puts("************");
for (int i = 1; i <= n; i ++)
{
for (int j = 1; j <= c; j ++)
printf("%d ", x[i][j]);
puts("");
}
puts("************");
}
void trackback(int i, int j, int f)
{
if(i <= 0 || j <= 0) return;
if(f == 0){
printf("不选第%d件商品\n", i);
trackback(i - 1, j, x[i - 1][j]);
}
if(f == 1){
printf("选第%d件商品\n", i);
trackback(i - 1, j - w[i], x[i - 1][j - w[i]]);//选这件商品后的坐标需要算一下
}
}
int main()
{
scanf("%d%d", &n, &c);
for (int i = 1; i <= n; i ++) scanf("%d", &w[i]);
for (int i = 1; i <= n; i ++) scanf("%d", &v[i]);
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= c; j ++){
if(w[i] <= j && dp[i - 1][j] < dp[i - 1][j - w[i]] + v[i]){
dp[i][j] = dp[i - 1][j - w[i]] + v[i];
x[i][j] = 1;
}
else{
dp[i][j] = dp[i - 1][j];
x[i][j] = 0;
}
}
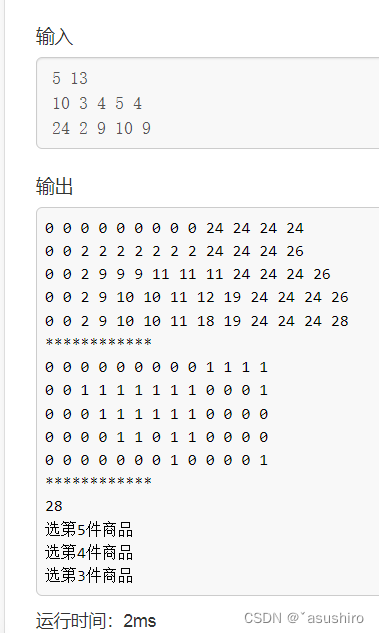
out();
printf("%d\n", dp[n][c]);
trackback(n, c, x[n][c]);
return 0;
}

下一篇
算法设计与分析复习–贪心(一)