【GCN】GCN学习笔记一

谱域图卷积
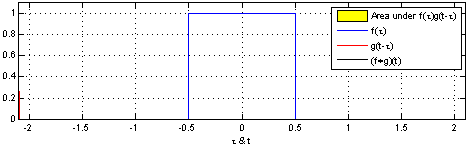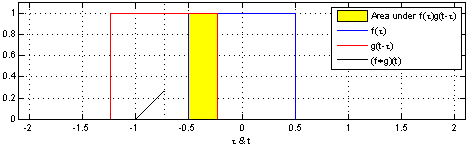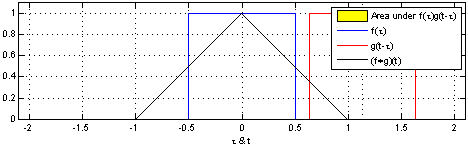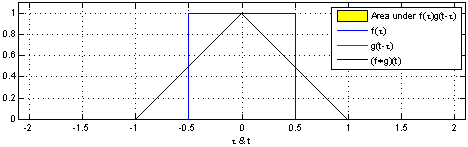
- 卷积
  - 卷积定义
  - 离散空间的卷积
- 图卷积简介
  - 卷积定理
  - 谱域图卷积实现思路
  - 如何定义图上的傅里叶变换
  - 拉普拉斯矩阵（Laplacian Matrix）
  - 拉普拉斯矩阵的性质
  - 拉普拉斯矩阵的谱分解
  - 拉普拉斯矩阵与拉普拉斯算子
- 图傅里叶变换
  - 图上的信号表示
  - 经典傅里叶变换
  - 特征向量基的性质
- 总结
- 三个经典图谱卷积模型
  - SCNN
  - ChebNet
  - GCN

谱域图卷积

卷积

卷积定义

卷积是分析数学中一种重要的运算，设 $f (x)$ 和 $g (x)$ 是 $\mathbb{R}$ 上的可积函数，连续形式的卷积定义如下：

$\int_{-\infin} ^{\infin} f(\tau) g(x - \tau) d\tau {\tag{1}}$

不同的函数和不同的卷积核可以的到不同的卷积结果。

离散空间的卷积

$y_n = x * w = \sum_{k=1}^k w_k x_{n-k} \tag{2}$
请添加图片描述

图卷积简介

经典卷积网络无法处理图结构数据。目前图卷积实现思路：

谱域图卷积
空域图卷积

卷积定理

两个信号在空域的卷积的傅里叶变换等于两个信号在频域中的傅里叶变换的点乘，点乘（element-wise multiplication）是指对两个矩阵、向量或序列中的相应元素进行相乘运算。即：
$\mathcal{F} [f_1(t)\star f_2(t)] = F_1(w) . F_2(w) \tag{3}$

$f_1(t)$ 和 $f_2(t)$ 是空域的两个信号
$F_1(w)$ 和 $F_2(w)$ 是频域的两个信号
$\star$ 表示卷积操作
$\mathcal{F}$ 表示傅里叶变换
$. $ 表示乘积操作

也可以写成：
$f_1(t)\star f_2(t) = \mathcal{F}^{-1} [F_1(w) . F_2(w)] \tag{4}$

$\mathcal{F}^{-1}$ 表示傅里叶逆变换

谱域图卷积实现思路

将图信号 $x$ 和卷积核 $w$ 做傅里叶变换，得到频域信号 $X$ 和 $W$
将频域信号 $X$ 和 $W$ 做乘积操作，得到频域信号 $Y$
将频域信号 $Y$ 做傅里叶逆变换，得到图信号 $y$
$y$ 即为图信号 $x$ 和卷积核 $w$ 卷积的结果

如何定义图上的傅里叶变换

基于图谱理论，图上的傅里叶变换使用图傅里叶变换（Graph Fourier Transform，GFT）来定义。GFT 的定义如下：
$\mathcal{F}_G(x) = U^T x \tag{5}$

$x$ 是图信号
$U$ 是图的特征向量矩阵

写成分量求和的形式为：
$\sum_{k=1}^N u_l(i)\hat{x}(\lambda_l) \tag{6}$

$x (i)$ 表示图信号 $x$ 在节点 $i$ 处的值
$u_l(i)$ 表示图的特征向量矩阵 $U$ 的第 $l$ 列的第 $i$ 个元素
$\hat{x}(\lambda_l)$ 表示图信号 $x$ 在特征值 $\lambda_l$ 处的值

拉普拉斯矩阵（Laplacian Matrix）

拉普拉斯矩阵是图信号处理中的一个重要概念，它是图信号的频域表示。拉普拉斯矩阵的定义如下：
$\tag{7}$

$D$ 是度矩阵， $D_{ii} = \sum_j A_{ij}$
$A$ 是邻接矩阵， $A_{ij} = 1$ 表示节点 $i$ 和节点 $j$ 之间有边，否则 $A_{ij} = 0$
$L$ 是拉普拉斯矩阵，否则 $L_{ij} = 0$ ，$。

拉普拉斯矩阵计算示例
在这里插入图片描述

$L_{ij} = -1$ 表示节点 $i$ 和节点 $j$ 之间有边
$L_{ii} = D_{ii}$ 拉普拉斯对角线值等于度矩阵对角线值
$L_{ij} = 0$ 表示节点 $i$ 和节点 $j$ 之间没有边

拉普拉斯矩阵的性质

拉普拉斯矩阵是半正定矩阵，即 $x^T L x \geq 0$ ，其中 $x$ 是任意向量。证明过程：
$x^T L x = x^T D x - x^T A x = \sum_{i=1}^N d_i x_i^2 - \sum_{i,j=1}^N a_{ij} x_i x_j = \frac{1}{2} \sum_{i,j=1}^N a_{ij} (x_i - x_j)^2 \geq 0 \tag{8}$

n 阶对称矩阵一定有 n 个线性无关的实特征值
对称矩阵的不同特征值对应的特征向量相互正交，这些拯救的特征向量构成的矩阵为正交矩阵
拉普拉斯矩阵的特征值都是非负的，且至少有一个特征值为 0
拉普拉斯矩阵的特征值为 0 的特征向量对应的是图的连通分量的个数，即 $L$ 的零特征值的个数等于图的连通分量的个数。

拉普拉斯矩阵的谱分解

特征分解(Eigen decomposition),又称为谱分解(Spectral decomposition)，是线性代数中的一个分解，将一个矩阵分解为特征向量和特征值的形式。拉普拉斯矩阵的谱分解如下：
$\Lambda U^T \tag{9}$

$U$ 是拉普拉斯矩阵的特征向量矩阵
$\Lambda$ 是拉普拉斯矩阵的特征值矩阵
$U^T$ 是 $U$ 的转置矩阵

对拉普拉斯谱分解后，n阶对称矩阵一定有n个线性无关的特征向量相互正交，这些正交的特征向量构成的矩阵为正交矩阵。因此，拉普拉斯矩阵的特征向量矩阵 $U$ 是正交矩阵，即 $U^T U = I$ ，其中 $I$ 是单位矩阵。

拉普拉斯矩阵与拉普拉斯算子

拉普拉斯矩阵与拉普拉斯算子是两个不同的概念，但是它们之间有一定的联系。拉普拉斯算子的定义如下：
$\Delta f = \nabla \cdot \nabla f = \sum_{i=1}^n \frac{\partial^2 f}{\partial x_i^2} \tag{10}$

$\nabla$ 是梯度算子
$\nabla \cdot$ 是散度算子
$\Delta$ 是拉普拉斯算子
$f$ 是函数
$x_i$ 是第 $i$ 个自变量
$n$ 是自变量的个数
$\frac{\partial^2 f}{\partial x_i^2}$ 是函数 $f$ 对自变量 $x_i$ 的二阶偏导数
$\sum_{i=1}^n \frac{\partial^2 f}{\partial x_i^2}$ 是函数 $f$ 对所有自变量的二阶偏导数之和
$\Delta f$ 是函数 $f$ 的拉普拉斯算子

图信号的拉普拉斯算子的定义如下：
$\Delta_G f = U \Delta f = U \nabla \cdot \nabla f = U \sum_{i=1}^n \frac{\partial^2 f}{\partial x_i^2} \tag{11}$

$\Delta_G f$ 是图信号 $f$ 的拉普拉斯算子
$U$ 是拉普拉斯矩阵的特征向量矩阵
$\Delta f$ 是函数 $f$ 的拉普拉斯算子
$\nabla \cdot \nabla f$ 是函数 $f$ 的拉普拉斯算子

对以上的公式如何得到呢？对于二维图像的拉普拉斯算子，我们可以将其写成如下的形式：
$\Delta f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} \tag{12}$
离散形式的拉普拉斯算子可以写成如下的形式：
$\Delta f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} = \frac{f(x+1,y) + f(x-1,y) - 2f(x,y)}{h^2} + \frac{f(x,y+1) + f(x,y-1) - 2f(x,y)}{h^2} \tag{13}$
其中 $h$ 是步长。将上式写成矩阵形式：
$\Delta f = \frac{1}{h^2} \begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} f(x-1,y) \\ f(x,y) \\ f(x+1,y) \end{bmatrix} + \frac{1}{h^2} \begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} f(x,y-1) \\ f(x,y) \\ f(x,y+1) \end{bmatrix} \tag{14}$

我们这里令 h = 1，将上式写成矩阵卷积形式：

$\Delta f(x) = \begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix} \star f(x) \tag{16}$
可以看出，二维图像的拉普拉斯算子，等于周围节点和自身节点的差值的和。对于图信号的拉普拉斯算子，节点的拉普拉斯算子，可以定义为与其相连节点与自身节点的差值的和，我们可以将其写成如下的形式：
$\Delta_G f = \sum_{j=1}^N A_{ij} (f_i - f_j) = \sum_{j=1}^N A_{ij} f_i - \sum_{j=1}^N A_{ij} f_j = \sum_{j=1}^N A_{ij} f_i - \sum_{j=1}^N A_{ji} f_j \tag{17}$

$A_{ij}$ 表示节点 $i$ 和节点 $j$ 之间的边的权重
$f_i - f_j)$ 表示节点 $i$ 和节点 $j$ 之间的差值

写成矩阵形式有：
$\begin{aligned} \Delta_G f =& \begin{bmatrix} \Delta f_1 \\ \Delta f_2 \\ \vdots \\ \Delta f_N \end{bmatrix} = & \begin{bmatrix} A_{11}f_1 - \sum_{j=1}^N A_{1i} f_j \\ \vdots \\ A_{nn}f_n - \sum_{j=1}^N A_{Ni} f_j \\ \end{bmatrix} = & Df - Af =Lf\tag{18} \end{aligned}$

$L$ 为拉普拉斯矩阵
对信号 $f$ 左乘一个拉普拉斯矩阵可以得到信号 $f$ 的拉普拉斯算子。

图傅里叶变换

图上的信号表示

图上的信号一般表达为一个向量。假设有n个节点。图上的信号记为：
$\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \tag{19}$

$x_i \in \mathbb{R}$ 表示节点 $i$ 上的信号.

经典傅里叶变换

经典傅里叶变换的定义如下：
傅里叶变换公式如下：
$X(\omega) = \int_{-\infin}^{\infin} x(t) e^{-j \omega t} dt \tag{20}$
离散傅里叶变换公式如下：
$X(\omega) = \sum_{n=0}^{N-1} x(n) e^{-j \omega n} \tag{21}$

经典傅里叶变换，是将一个函数表示成了一个若干个正交基函数的线性组合。对于图上的信号，如果要进行一个傅里叶变换，很自然的我们想到，我们也要找到一组正交基，通过这组正交基的线性组合来表达图上的信号。

矩阵形式为：
$\hat{x} \tag{23}$

$x$ 表示图上的信号
$U$ 表示图的特征向量矩阵
$\hat{x}$ 表示图信号 $x$ 的傅里叶系数

如何求 $\hat{x}$ 呢？我们可以将上式两边同时左乘 $U^T$ ，得到：
$U^T x = U^T U \hat{x} = I \hat{x} = \hat{x} \tag{24}$

$I$ 表示单位矩阵
$\hat{x}$ 表示图信号 $x$ 的傅里叶系数
$U$ 表示图的特征向量矩阵
$x$ 表示图上的信号
$U^T$ 表示 $U$ 的转置矩阵

因此，我们可以得到：
$\hat{x} = U^T x \tag{25}$

$\hat{x}$ 表示图信号 $x$ 的傅里叶系数
$U$ 表示图的特征向量矩阵
$x$ 表示图上的信号
$U^T$ 表示 $U$ 的转置矩阵
$\hat{x}$ 表示图信号 $x$ 的傅里叶系数

特征向量基的性质

拉普拉斯矩阵的特征值担任了和频率类似的位置。
- 特征值越大，对应的特征向量的频率越高。
- 特征值越小，对应的特征向量的频率越低。
- 特征值为 0 的特征向量对应的是图的连通分量的个数，即 $L$ 的零特征值的个数等于图的连通分量的个数。
拉普拉斯矩阵的特征向量担任了基函数的位置。
- 0特征值对应一个常数特征向量，这个和傅里叶变换中的常数项类似。
- 低特征值对应的特征向量比较平滑，高特征值对应的特征向量变换比较剧烈。两者对应于低频基函数和高频基函数。

如何理解这两个结论呢？
我们使用图拉普拉斯的二次型(graph Laplacian quadratic form) 来定义信号的平滑程度。其表示有边相连的两个节点信号的平方差乘以权重的求和，其值越小，代表越平滑

$x^{\top} L x = \frac{1}{2}\sum_{i,j=1}^N A_{ij} (x_i - x_j)^2 \tag{28}$

又因为
$x^{\top} L x = x^{\top} U \Lambda U^{\top} x = \hat{x}^{\top} \Lambda \hat{x} = \sum_{k=1}^N \lambda_k \hat{x}^2(\lambda_k) \tag{29}$
所以对应特征值越小，对应的特征向量越平滑。

总结

利用图傅里叶变换，可以将定义在图节点上的信号 $x\in\mathbb{R}^n$ 从空间域转换到谱域。

空间域到谱域的变换： $x\rightarrow \hat{x} = U^T x$
谱域到空间域的变换： $\hat{x} \rightarrow x = U \hat{x}$
其中 $\Lambda U^{-1}$

卷积定理

空间域的卷积定理： $x\star h \rightarrow X(\omega) H(\omega)$

$\star g = \mathcal{F}^{-1} \odot [X(\omega) H(\omega)] = U(U^{\top}x \odot U^{\top}g) \tag{30}$
如果以矩阵乘法的形式表达这个公式，去掉 harmand 乘积。同时，通常我们并不关心空间域上的滤波器信号g是什么样子，只关心其在频率域的情况。
令
$g_{\theta} = (U^{\top}g) = \text{diag} (\lambda g) =\text{diag} (\hat(\lambda))$

则公式等价转换成下式：
$\star g =U \text{diag}(\hat{g}) U^{\top} x \tag{31}$

$\text{diag}(\hat{g}(\lambda_i))$ 是谱域卷积的一个分量。

三个经典图谱卷积模型

卷积网络中不同层的特征图：
在这里插入图片描述

SCNN

核心思想：

用可学习的对角矩阵来替代谱域的卷积核，从而实现图卷积操作。

ChebNet

Chebyshev多项式
Chebyshev多项式是一类具有重要应用的正交多项式，其定义如下：
$T_0(x) = 1, T_1(x) = x, T_{n+1}(x) = 2xT_n(x) - T_{n-1}(x) \tag{32}$

矩阵形式为：
$T_0(L) = I, T_1(L) = L, T_{n+1}(L) = 2LT_n(L) - T_{n-1}(L) \tag{32}$

多项式插值：
$\sum_{k=0}^{K-1} \alpha_k x^{k-1} \tag{33}$
切比雪夫插值将幂函数换成了切比雪夫多项式的项：
$\sum_{k=0}^{K-1} \alpha_k T_k(x) \tag{34}$

ChebNet的核心思想：

利用切比雪夫多项式来近似谱域的卷积核，从而实现图卷积操作。
利用切比雪夫多项式的递归性质，可以将谱域的卷积核的近似程度控制在任意的精度范围内。

$\begin{aligned} x \star g_{\theta} =& Ug_{\theta}U^{\top}x \\ =& U \sum_{k=0}^{K}\beta_k T_k(\Lambda) U^{\top} x \\ =& \sum_{k=0}^{K}\beta_k T_k(L)(U \Lambda U^{\top}) x \\ =& \sum_{k=0}^{K}\beta_k T_k(L) x \\ \end{aligned} \tag{35}$

卷积核只有 K+1个可学习的参数，一般 k 远小于 n, 因此参数量大大减少。
采用切比雪夫多项式代替谱域的卷积后，不需要特征值分解了。
卷积核又严格的空间局部性，同时，k就是卷积核的感受野半径。即中心顶点K阶最邻近节点作为领域节点。
这样我们就可以不用去计算拉普拉斯分解，直接使用拉普拉斯矩阵来进行卷积操作了。

GCN

GCN的核心思想：

利用一阶切比雪夫多项式来近似谱域的卷积核，从而实现图卷积操作。
利用一阶切比雪夫多项式的递归性质，可以将谱域的卷积核的近似程度控制在任意的精度范围内。

$\begin{aligned} x \star g_{\theta} =& Ug_{\theta}U^{\top}x \\ =& \sum_{k=0}^{k}\beta_k T_k(\hat{L})x \\ =& \sum_{k=0}^1 \beta_k T_k(\hat{L})x \\ =& \beta_0 T_0(\hat{L})x + \beta_1 T_1(\hat{L})x \\ =& (\beta_0 + \beta_1 \hat{L})x =& (\beta_0 + \beta_1(L - I_n))x \\ =& (\beta_0 - \beta_1(D^{-1/2WD^{-1/2}}))x \\ =& (\theta(D^{-1/2WD^{-1/2}} + I_n))x \\ \end{aligned} \tag{36}$