一、配置虚拟环境
1、安装虚拟环境库vitualenv 与vitualenvwrapper-win
2、创建虚拟环境 myenv
3、在此环境中安装django
二、创建一个Django项目
1、使用命令来创建:django-admin startproject Django2023 工程名为Django2023
2、 使用PyCharm专业版创建Django项目
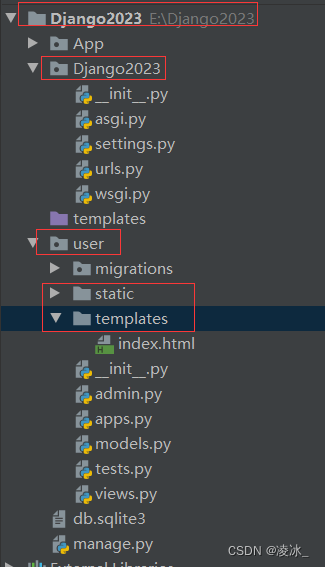
|Django2023 项目根目录
├── user 应用名称
│ ├── migrations 数据模型迁移记录目录
│ │ └── __init__.py inti文件,标识当前所在的数据模型迁移记录目录是一个 │ ├──templates 模板资源(自己创建)│ ├──static 静态资源(自己创建)
│ ├── __init__.py init文件,标识当前所在的应用目录是一个 Python 包
│ ├── admin.py Django Admin 应用的配置文件
│ ├── apps.py 应用程序本身的属性配置文件
│ ├── models.py 用于定义应用中所需要的数据表的配置文件
│ ├── tests.py 用于编写当前应用程序的单元测试的测试文件
│ └── views.py 用来定义视图处理函数的文件
├── Django2023 项目名称
│ ├── __init__.py init文件,标识当前所在的项目目录是一个 Python 包
│ ├── settings.py 项目配置文件
│ ├── urls.py url路径文件
│ └── wsgi.py WSGI服务器程序的入口文件
└── manage.py 命令行工具文件
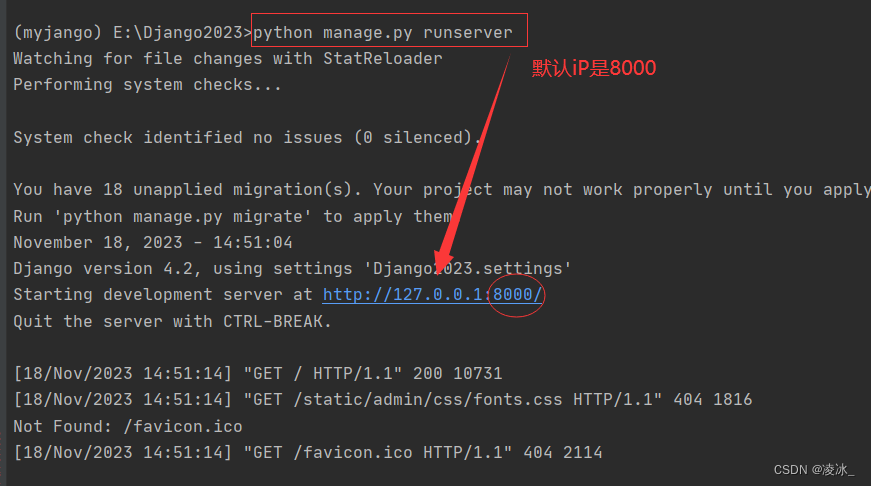
3、测试服务器启动
1) 使用PyCharm专业版启动
2) 使用命令执行启动
python manage.py runserver [ip:port]
直接运行,默认的端口:8000
修改端口号: python manage.py runserver 8008

退出运行:ctrl+C

4、数据迁移
迁移:就是将模型映射到数据库的过程
生成迁移文件
python manage.py makemigrations
执行迁移
python manage.py migrate

注意:配置数据库(使用默认的SQLite)
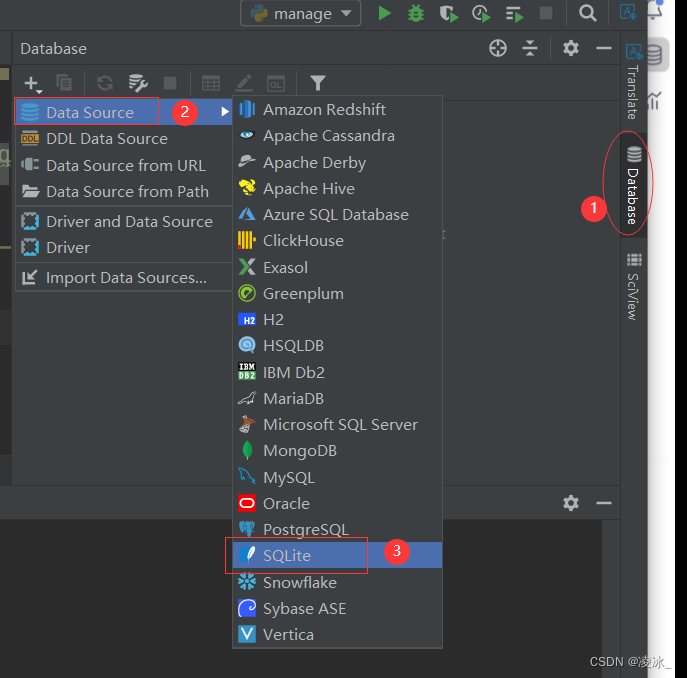
选择SQLite
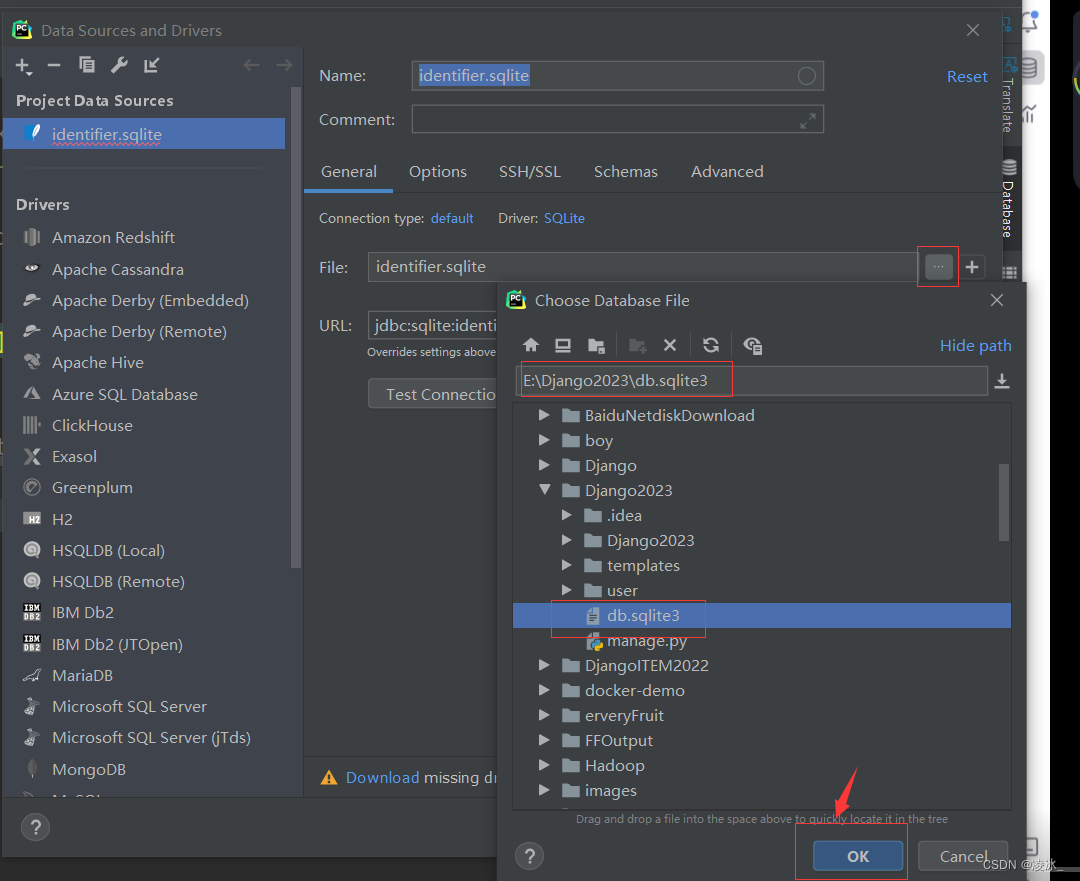
测试配置的数据库

打开数据库
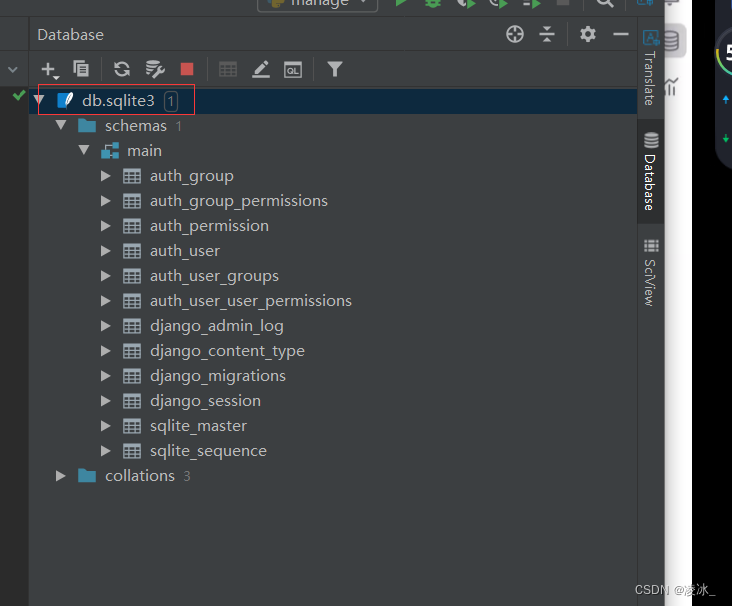
5、创建子应用
python manage.py startapp App(子应用名称)
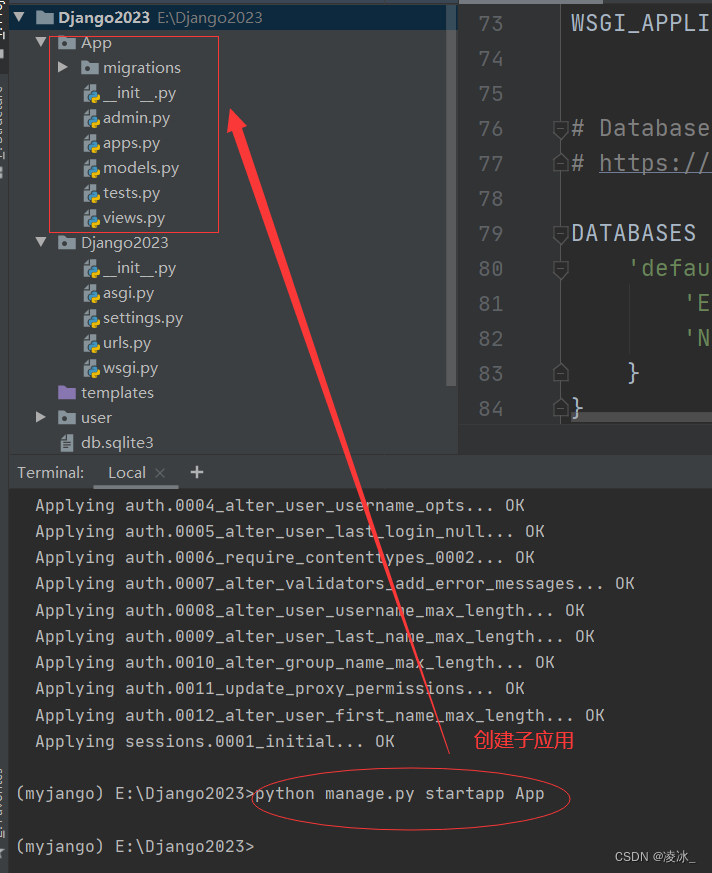
6、基本视图
(1)在views.py文件中 写视图函数
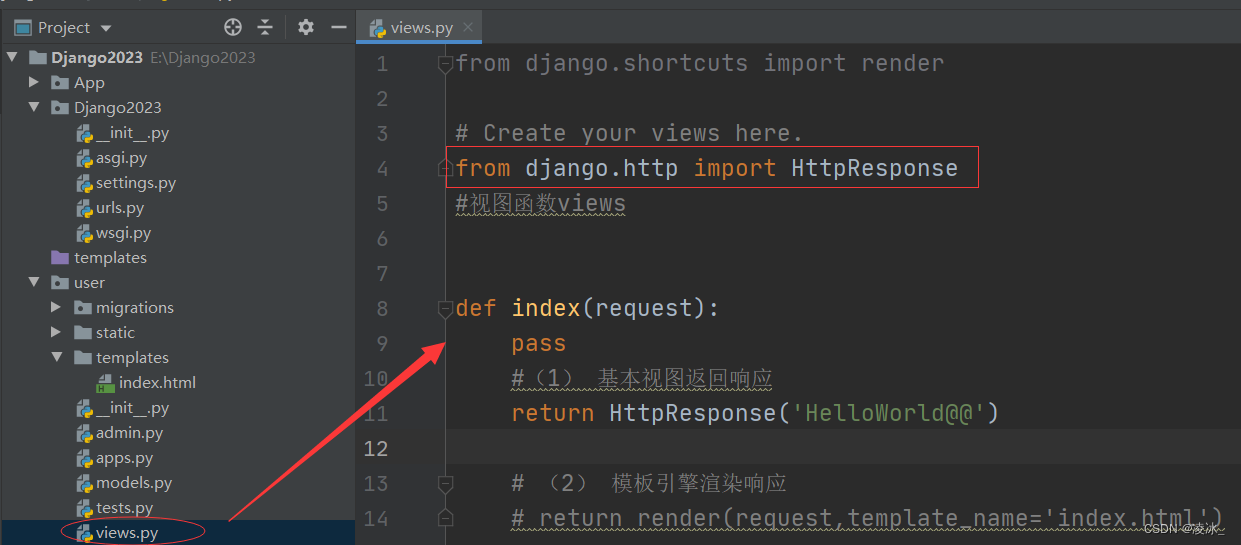
(2)配置urls
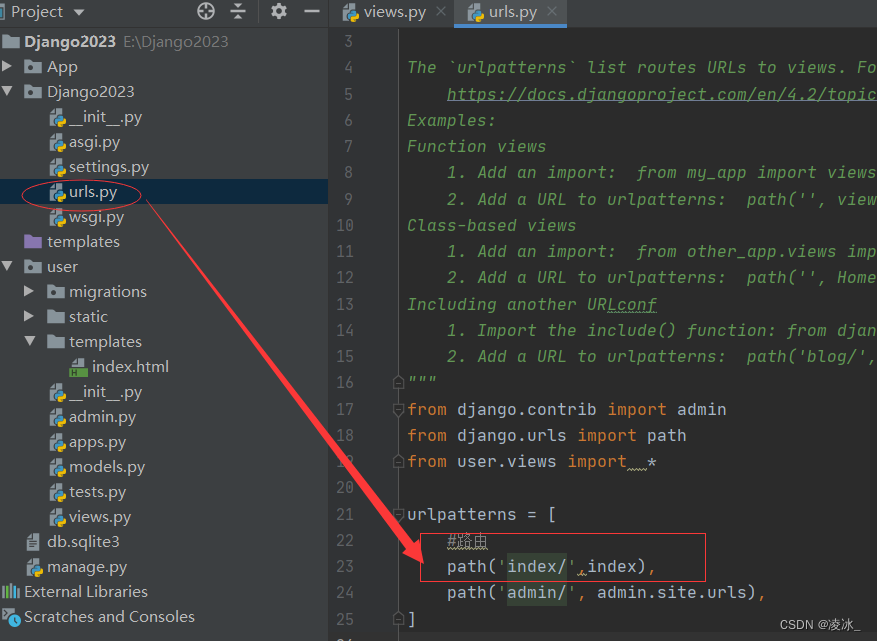
(3) 测试
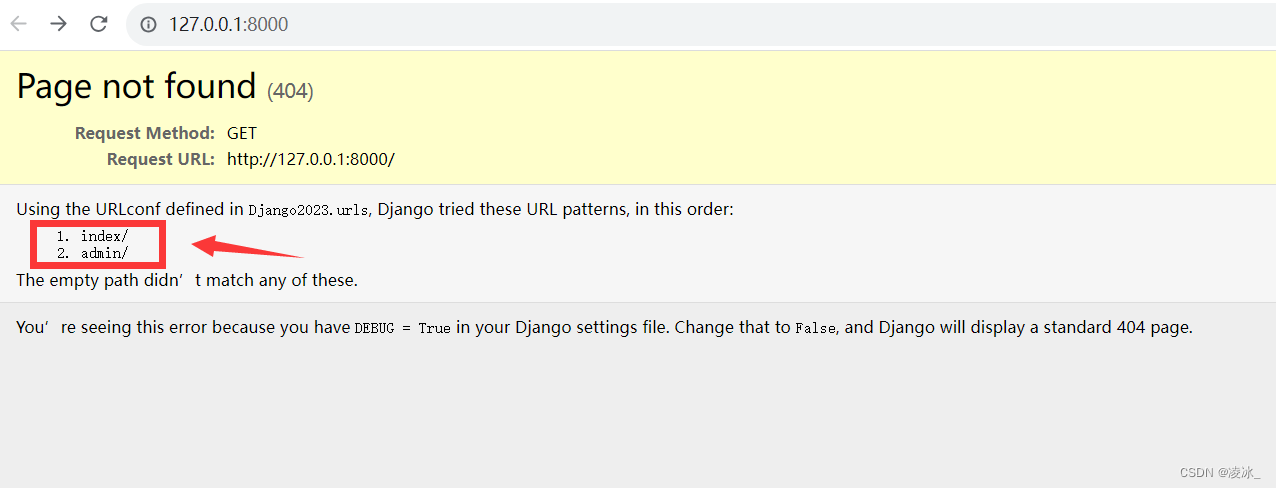
(4) 访问页面:localhost:8000/index/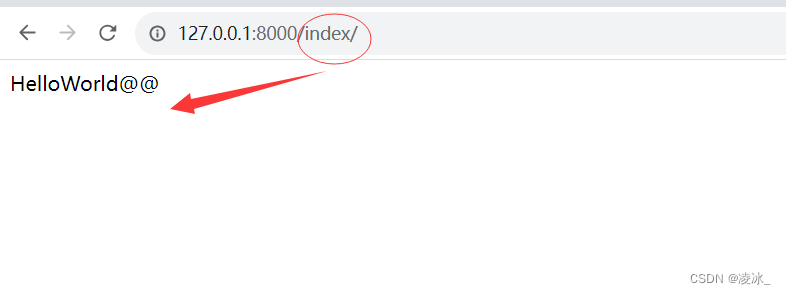
7、基本模板
(1) 在views.py文件
from django.shortcuts import render
# Create your views here.
from django.http import HttpResponse
#视图函数views
def index(request):
pass
# (2) 模板引擎渲染响应
return render(request,template_name='index.html')(2)创建templates目录下创建html文件

(3)配置urls (同上)
(4) 访问页面:localhost:8000/index/
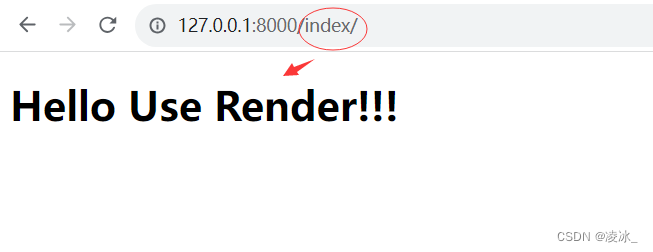
如何在模板中加载图片展示
(1)同7操作一样
(2)创建static目录下存放图片目录imgs下pic.png图片
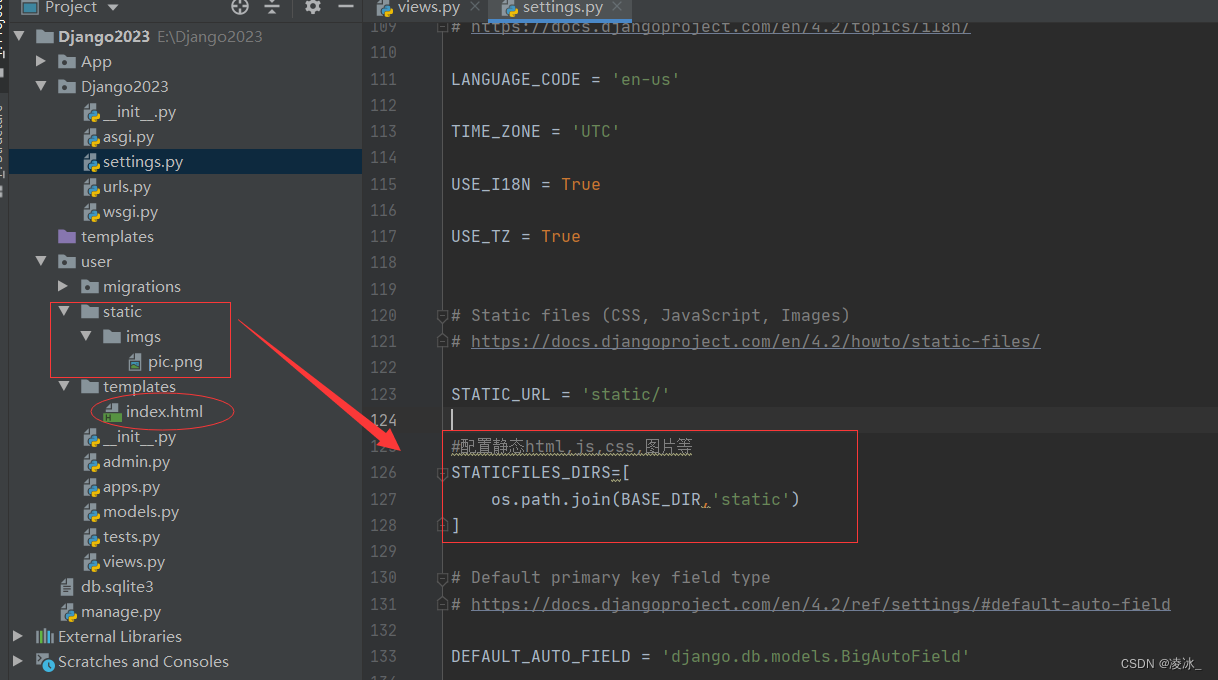
(3)在setting中配置静态资源(图片如上)
#配置静态html,js,css,图片等
STATICFILES_DIRS=[
os.path.join(BASE_DIR,'static')
]
(4)在index.html文件中进行图片加载
{% load static %}
{#在模板中加载自定义标记#}
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>渲染模板</title>
</head>
<body>
<h1>Hello Use Render!!!</h1>
<img src="{% static 'imgs/pic.png' %}">
bear!!!
</body>
</html>(5)运行效果