文章目录
- 10 回环检测
- 10.1 概述
- 10.1.1 回环检测的意义
- 10.1.2 回环检测的方法
- 10.1.3 准确率和召回率
- 10.2 词袋模型
- 10.3 字典
- 10.3.1 字典的结构
- 10.3.2 实践:创建字典
- 10.4 相似度计算
- 10.4.1 理论部分
- 10.4.2 实践:相似度的计算
- 10.5 实验分析与评述
10 回环检测
10.1 概述
10.1.1 回环检测的意义
前端提供特征点的提取和轨迹、地图的初值,后端负责数据的优化。但是如果像视觉里程计那样只考虑相邻时间上的关键帧,则会出现累积误差,无法构建全局一致的轨迹和地图。

回环检测的关键是 有效地检测出相机经过同一个地方 这件事。
10.1.2 回环检测的方法
(1)大体有两种思路:基于里程计的几何关系和基于外观的几何关系。
(2)在基于外观的回环检测中,核心问题是 如何计算图像间的相似性。
10.1.3 准确率和召回率
| 算法/事实 | 是回环 | 不是回环 |
|---|---|---|
| 是回环 | 真阳性(TP) | 假阳性(FP) |
| 不是回环 | 假阴性(FN) | 真阴性(TN) |
假阳性称为 感知偏差,假阴性称为 感知变异。
定义准确率和召回率:
Precision = T P / ( T P + F P ) , Recall = T P / ( T P + F N ) (10-1) \text { Precision }=\mathrm{TP} /(\mathrm{TP}+\mathrm{FP}), \quad \text { Recall }=\mathrm{TP} /(\mathrm{TP}+\mathrm{FN}) \tag{10-1} Precision =TP/(TP+FP), Recall =TP/(TP+FN)(10-1)
准确率描述的是算法提取的所有回环中确实是真实回环的概率;而召回率是指在所有真实回环中被检测出来的概率。他们通常是一对矛盾。SLAM 中,我们对准确率的要求更高,而对召回率相对宽容一些。
10.2 词袋模型
词袋(Bag-of-Words, BoW)用 图像上有哪几种特征 来描述图像。例如图像上有一只狗、一辆车等等。具体有以下三步:
-
确定 “人”、“狗”、“车”等概念——对应于 BoW 中的单词,许多单词构成字典;
-
确定图像中出现了哪些字典中定义了的概念——用单词出现的情况(或直方图)来描述整幅图像,这样就把图像转换成了一个向量的描述;
-
比较两幅图像描述的相似程度。
根据各类特征出现的次数,可将该图像表示为 [ w 1 , w 2 , . . . , w n ] T [w_1,w_2,...,w_n]^{\mathrm{T}} [w1,w2,...,wn]T;如果仅考虑特征是否出现,也可以只用 0、1 组成的向量表示。
假设两幅图像的描述向量分别为 a \boldsymbol{a} a 、 b \boldsymbol{b} b,则其相似度表示为
s ( a , b ) = 1 − 1 W ∥ a − b ∥ 1 (10-1) s(\boldsymbol{a},\boldsymbol{b})=1-\frac{1}{W}\|\boldsymbol{a}-\boldsymbol{b}\|_1 \tag{10-1} s(a,b)=1−W1∥a−b∥1(10-1)
其中, W W W 为总的单词数量;范数为 L 1 L_1 L1 范数,即各元素绝对值之和。那么,当两个向量相同时,得到 1,而两个向量完全相反时,值为 0。
10.3 字典
10.3.1 字典的结构
一个单词和一个单独的特征点不同,它是某一类特征的组合,所以字典生成问题类似 聚类 问题。
(1)假设我们对大量的图像提取了特征点,例如有 N N N 个,希望构建一个有 k k k 个单词的字典,每个单词可以看做局部相邻特征点的集合,可以用 K-means 算法聚类,步骤如下:
① 随机选取 k k k 个中心点: c 1 , c 2 , . . . , c k c_1,c_2,...,c_k c1,c2,...,ck;
② 对每一个样本,计算它与每个中心点之间的距离,取最小的作为它的归类;
③ 重新计算每个类的中心点;
④ 如果每个中心点都变化很小,则算法收敛,退出;否则返回第二步。
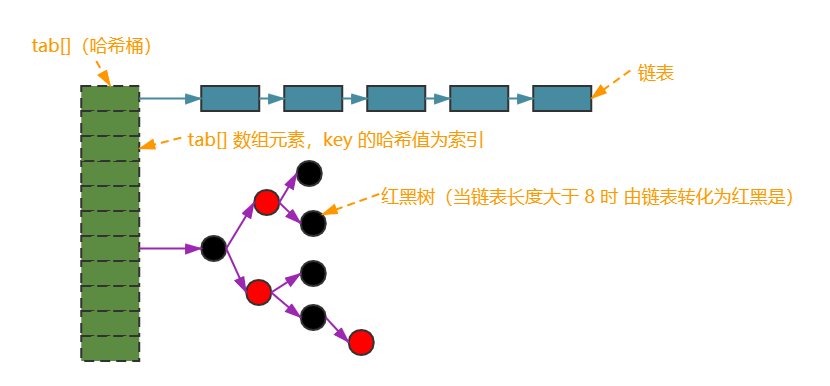
(2)实践中,我们通常会构建一个很大的字典,这时,各个单词之间的比较就会变得很麻烦和低效。于是,提出采用 k k k 叉树来表达字典,类似于层次聚类,是 K-means 算法的直接扩展。假设有 N N N 个特征点,希望构建一个深度为 d d d 、每次分叉为 k k k 的树,步骤如下:
① 在根节点,用 K-means 把所有样本聚成 k k k 类(实际中为保证聚类均匀性会使用 K-means++ 算法),这样得到第一层;
② 对第一层的每个节点,把属于该节点的样本再次聚成 k k k 类,得到下一层;
③ 以此类推,最后得到叶子层。叶子层即为所谓的 Words。
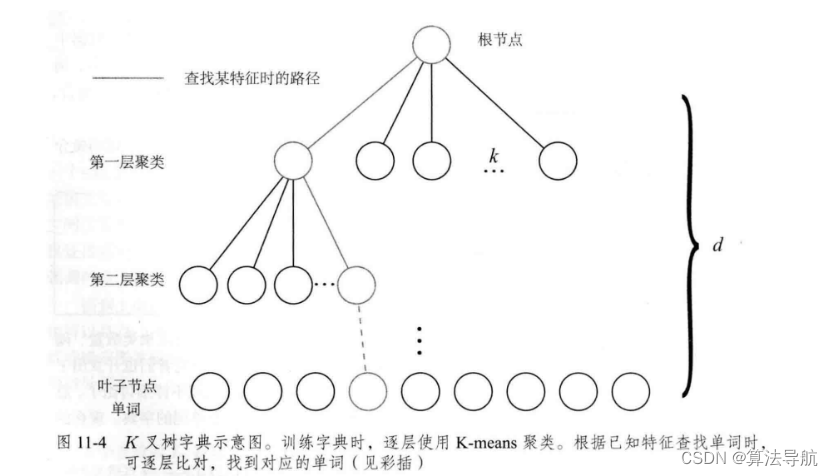
最终我们在叶子层构建了单词,而树结构中的中间节点仅供快速查找时使用。这样一个深度为 d d d 、分叉为 k k k 的树,可以容纳 k d k^d kd 个单词。在查找某个给定特征对应的单词时,只需将它与每个中间节点的聚类中心比较(一共 k k k 次),即可找到最后的单词,保证了对数级别的查找效率。
10.3.2 实践:创建字典
10.4 相似度计算
10.4.1 理论部分
有一些 Word 很常见,另一些则很罕见,因此有必要对单词的区分度或重要性加以评估。采用 TF-IDF(译频率-逆文档频率)进行加权,TF 部分的思想是,某单词在一幅图像中经常出现,它的区分度就高;IDF 部分的思想是,某单词在字典中出现的频率越低,则区分度越高。
- TF 部分需要对图像的特征进行计算,它是指某个单词在单幅图像中出现的频率:假设图像 A A A 中单词 w i w_i wi 出现了 n i n_i ni 次,而该图像中所有单词出现的次数总和为 n n n,则
T F i = n i n (10-2) \mathrm{TF}_i=\frac{n_i}{n} \tag{10-2} TFi=nni(10-2)
- IDF 部分可在字典训练过程中进行计算,它是指某个叶子节点 w i w_i wi 总的特征数量相对于所有特征数量的比例:假设有两幅图像,所有特征数量为 n n n,其中 w i w_i wi 特征数量为 n i n_i ni,则
I D F i = ln n n i (10-3) \mathrm{IDF}_i=\ln {\frac{n}{n_i}} \tag{10-3} IDFi=lnnin(10-3)
T F i \mathrm{TF}_i TFi 和 I D F i \mathrm{IDF}_i IDFi 越大,单词的区分度越高。定义 w i w_i wi 的权重为
η i = T F i × I D F i (10-4) \eta_i=\mathrm{TF}_i \times \mathrm{IDF}_i \tag{10-4} ηi=TFi×IDFi(10-4)
那么,对于某幅图像 A A A ,组成它的 BoW 向量为:
A = [ ( w 1 , η 1 ) , ( w 2 , η 2 ) , … , ( w N , η N ) ] = def v A (10-5) A=\left[\left(w_{1}, \eta_{1}\right),\left(w_{2}, \eta_{2}\right), \ldots,\left(w_{N}, \eta_{N}\right)\right] \stackrel{\text { def }}{=} \boldsymbol{v}_{A} \tag{10-5} A=[(w1,η1),(w2,η2),…,(wN,ηN)]= def vA(10-5)
其中 w i w_i wi 为每个单词的索引, η i \eta_i ηi 为对应的权重,两幅图像的相似度评分公式可以为:
s ( v A − v B ) = 2 ∑ i = 1 N ( ∣ v A i ∣ + ∣ v B i ∣ − ∣ v A i − v B i ∣ ) (10-6) s(\boldsymbol{v}_A-\boldsymbol{v}_B)=2\sum_{i=1}^{N}(|\boldsymbol{v}_{Ai}|+|\boldsymbol{v}_{Bi}|-|\boldsymbol{v}_{Ai}-\boldsymbol{v}_{Bi}|) \tag{10-6} s(vA−vB)=2i=1∑N(∣vAi∣+∣vBi∣−∣vAi−vBi∣)(10-6)
这里是 L 1 L_1 L1 范数,也就是各元素的绝对值。