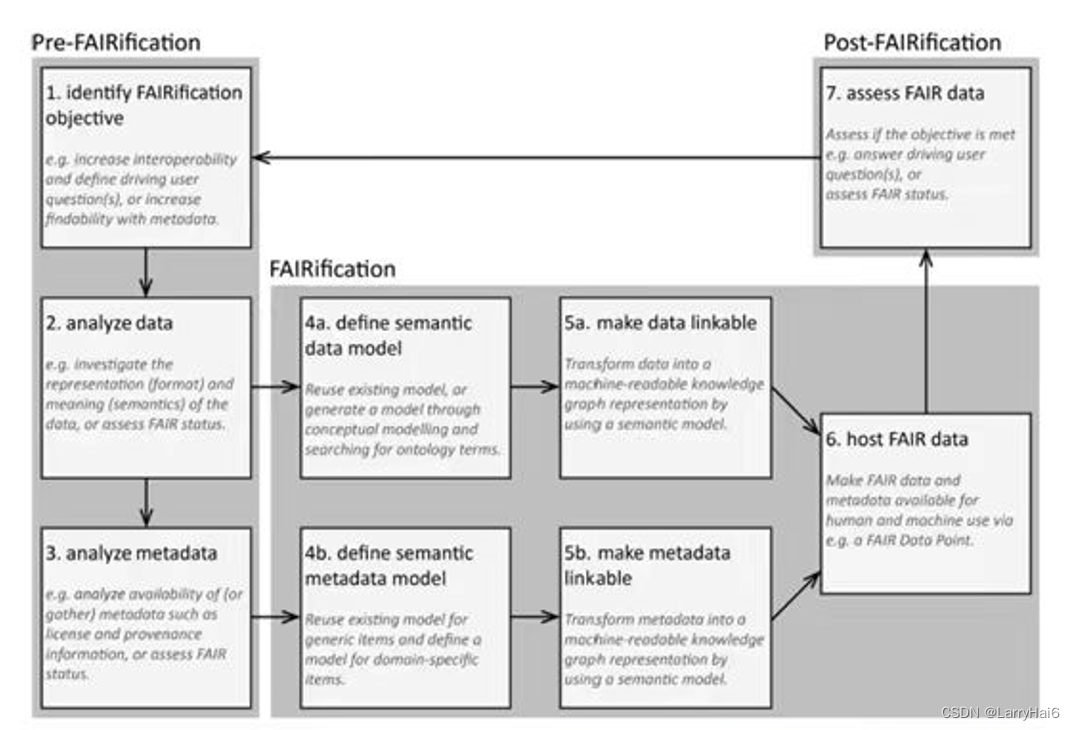
有向图:图中的每条边都有方向的图叫有向图。此时,边的两个顶点有次序关系,有向边 < u,v>成为从顶点u到顶点v的一条弧,u成为弧尾(始点),v成为弧头(终点),即有向图中弧 < u,v>和弧 < v,u> 表示不同的两条边。
无向图:图中的每条边没有方向的图。边的两个顶点没有次序关系,无向图用边(u,v)表示对称弧< u,v>和< v,u>。
权:图中的边或弧上有附加的数量信息,这种可反映边或弧的某种特征的数据成为权。
网:图上的边或弧带权则称为网。可分为有向网和无向网。
邻接和关联:若边e=(u,v)或弧e= < u,v>,则称点u和v互为邻接顶点,并称边e或弧e关联于顶点u和v。
度:在无向图中,与顶点v关联的边的条数成为顶点v的度。有向图中,则以顶点v为弧尾的弧的条数成为顶点v的出度,以顶点v为弧头的弧的条数成为顶点v的入度,而顶点v的度=出度+入度。图中各点度数之和是边(或弧)的条数的2倍。
圈:图中联接同一个顶点的边叫圈。
平行边:图中两个顶点之间若有两条或两条以上的边,称这些边为平行边。
简单图:没有圈也没有平行边的图。
有向完全图:有n个顶点,n(n-1)条弧的有向图。每两个顶点之间都有两条方向相反的边连接的图。
完全图:有n个顶点,n(n-1)/2条边的无向图。若一个图的每一对不同顶点恰有一条边相连,则称为完全图。完全图是每对顶点之间都恰连有一条边的简单图。
路径长度:路径上边或弧的数目。若路径上的各顶点均不相同,则称这条路经为简单路经(或路),除第一个和最后一个顶点相同外,其他各顶点均不相同的路径成为回路(或环)。
连通图:在无向图G中,对与图中的任意两个顶点u、v都是连通的,则称图G为连通图。
强连通图:在有向图G中,如果对于每一对Vi和Vj 属于顶点集V,Vi不等于Vj ,从Vi到Vj和从Vj到Vi都存在路径,则称G是强连通图。
强连通分量:有向图中的极大强连通子图称做有向图的强连通分量。
生成树:一个连通图的生成树是一个极小的连通子图,它含有图中全部的n个顶点,但只有足以构成一棵树的n-1条边。
有向树:如果一个有向图恰有一个顶点的入度为0,其余顶点的入度为1,则是一棵有向树。
图的存储结构
图的存储结构,常用的是”邻接矩阵”和”邻接表”。
邻接矩阵
邻接矩阵是指用矩阵来表示图。它是采用矩阵来描述图中顶点之间的关系(及弧或边的权)。
假设图中顶点数为n,则邻接矩阵定义为:

下面通过示意图来进行解释。

图中的G1是无向图和它对应的邻接矩阵。

图中的G2是无向图和它对应的邻接矩阵。
通常采用两个数组来实现邻接矩阵:一个一维数组用来保存顶点信息,一个二维数组来用保存边的信息。
邻接矩阵的缺点就是比较耗费空间。
邻接表
邻接表是图的一种链式存储表示方法。它是改进后的”邻接矩阵”,它的缺点是不方便判断两个顶点之间是否有边,但是相对邻接矩阵来说更省空间。

图中的G1是无向图和它对应的邻接矩阵。

图中的G2是无向图和它对应的邻接矩阵。
图的python实现
在Python中,图主要是通过列表和词典来构造。
实现的功能:
- 寻找一条路径
- 查找所有的路径
- 查找最短路径
'''
图的表示:
A --> B
A --> C
B --> C
B --> D
C --> D
D --> C
E --> F
F --> C
'''
#找一条路
def find_path(graph,start,end,path=[]):
path = path + [start]
if start == end:
return path
if start not in graph.keys():
return None
for node in graph[start]:
if node not in path:
newpath = find_path(graph,node,end,path)
if newpath:
return newpath
return path
if __name__ == '__main__':
graph = {'A': ['B', 'C'],
'B': ['C', 'D'],
'C': ['D'],
'D': ['C'],
'E': ['F'],
'F': ['C']}
print(find_path(graph,'A','D'))