论文作者：Robert G. Haight, Charles S. Revelle, Stephanie A. Snyder
论文原文：Robert G. Haight, Charles S. Revelle, Stephanie A. Snyder, (2000) An Integer Optimization Approach to a Probabilistic Reserve Site Selection Problem. Operations Research 48(5):697-708. https://doi.org/10.1287/opre.48.5.697.12411
前言：
神奇动物在哪里？随着人类生产生活行为的扩张，诸多生物濒危。建立自然保护区是保护濒危生物的有效举措，然而由于生产生活需要（例如耕地、建造城市等），我们不可能将所有的地方都选址为自然保护区。因此，我们亟需定量研究与优化这一选址问题。与此同时，大自然是一个复杂、优美的系统，充满了不确定性，如何在选址优化决策中考虑不确定性是一个重要的课题，也是难题。
本篇推文解读发表在utd24期刊《Operations Research》的一篇经典文章。第二作者Charles S. Revelle是美国科学院院士，在空间优化、选址等领域产出丰厚，也是著名的集合覆盖问题（Location Set Covering Problem, LSCP）的提出者，其学生也是桃李满天下。通过本文，你将了解到运筹学可以帮助我们解决生物保护这一看似陌生、却很重要的课题。同时，你将了解到考虑不确定性的选址优化决策模型，与一种模型线性化的方法。
1. 背景
随着人类生产生活行为的扩张，诸多生物濒危。据不完全统计，超过900个濒危物种已被列为或即将被列入美国联邦濒危物种法。
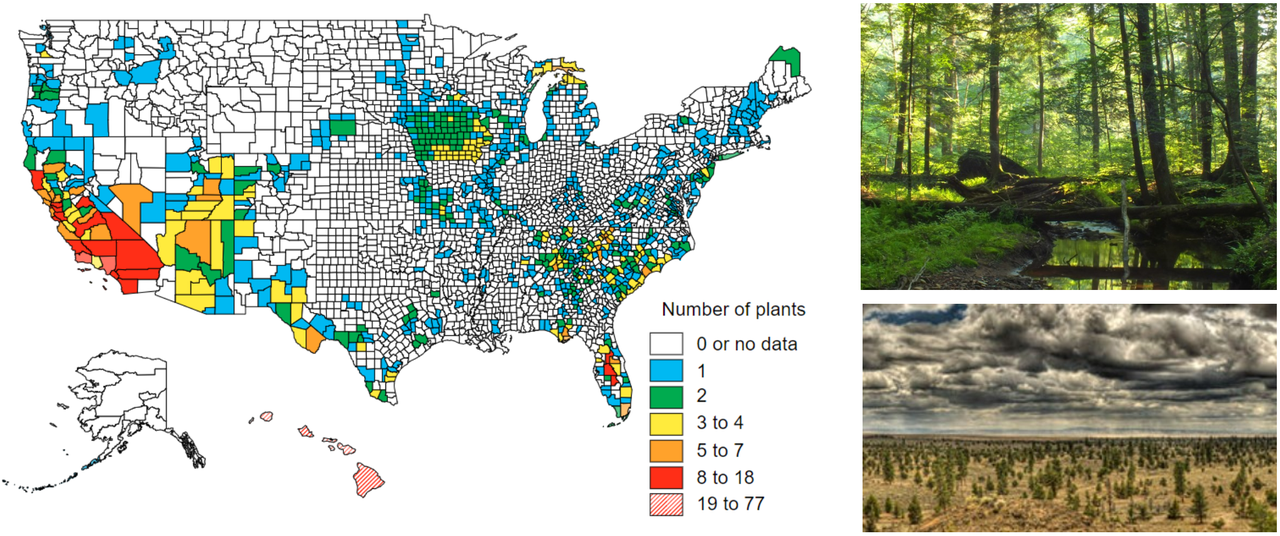
图1 美国濒危植物的地理分布。数据来源：Science期刊 [2]
建立自然保护区是保护濒危生物的有效举措。然而决策者需要充分权衡生产生活需要（例如耕地、建造城市等）与建立自然保护区的矛盾。随意划定自然保护区将无法有效保护濒危物种与实现生物多样性目标。因此，定量研究与优化方法亟需被引入来助力自然保护区的选址。
最基本的定量决策方法包括打分排序法、贪心启发式算法等。然而，我们希望更精准、更优的方式辅助我们进行定量决策。从运筹优化的视角，这一问题通常可以被建模为：在一定预算成本的限制下（约束条件），选择一个备选区域集合的子集（决策变量）组建自然保护区，以期实现最大化地保护关注的濒危生物（目标函数）。给定确定性的输入数据，可以应用或改进经典的选址模型来达成目标，例如集合覆盖问题（Location Set Covering Problem, LSCP）[3] 或最大覆盖问题（Maximum Covering Location Problem，MCLP）[4] 。
上述模型认为输入数据是确定性的。然而，大自然是一个复杂的不确定性系统，我们很难确定生物是否一定出现在某个自然保护区，这是一类概率数据。为了考虑这一不确定因素，本文针对性地设计了数学优化模型COMPRES（Covering Model for Probabilistic Reserve Selection）。
2. 模型构建
定义一些数学符号：集合 I I I表示被保护生物集合，其中 i ∈ I i\in I i∈I；集合 J J J表示备选区域集合，其中 j ∈ J j\in J j∈J； T T T表示自然保护区总面积的上界，其表征了预算成本； A j A_{j} Aj表示备选区域 j j j的面积； N i N_i Ni表示存在生物 i i i的备选区域集合，即生物 i i i在这些区域内出现的概率不为0； P i j P_{ij} Pij表示被保护生物 i i i出现在备选区域 j j j的概率； α i \alpha_i αi表示保护生物 i i i的可靠性阈值；0-1决策变量 X j X_j Xj表示区域 j j j是否被选为自然保护区的一部分，是为1，反之为0；0-1决策变量 Y i Y_i Yi表示生物 i i i是否被所设计的自然保护区以不低于 α i \alpha_i αi的可靠性保护，是为1，反之为0。
所设计的数学模型COMPRES如下：
max
Z
=
∑
i
∈
I
Y
i
\begin{equation} \max Z=\sum\limits_{i\in I}Y_i \end{equation}
maxZ=i∈I∑Yi
s
.
t
.
∑
j
∈
J
A
j
X
j
≤
T
,
∏
j
∈
N
i
(
1
−
P
i
j
)
X
j
≤
(
1
−
α
i
)
Y
i
,
∀
i
∈
I
,
1
−
(
∏
j
∈
N
i
(
1
−
P
i
j
)
X
j
)
≥
β
i
,
∀
i
∈
M
,
X
j
,
Y
i
∈
{
0
,
1
}
,
∀
i
∈
I
,
∀
j
∈
J
.
\begin{align} s.t. & \sum\limits_{j\in J}A_jX_j\leq T, \\ & \prod\limits_{j\in N_i}(1-P_{ij})^{X_j}\leq(1-\alpha_i)^{Y_i}, \forall i\in I, \\ & 1-\left(\prod\limits_{j\in N_i}(1-P_{ij})^{X_j}\right)\geq \beta_i, \forall i\in M, \\ & X_j, Y_i\in\{0,1\}, \forall i\in I, \forall j\in J. \end{align}
s.t.j∈J∑AjXj≤T,j∈Ni∏(1−Pij)Xj≤(1−αi)Yi,∀i∈I,1−
j∈Ni∏(1−Pij)Xj
≥βi,∀i∈M,Xj,Yi∈{0,1},∀i∈I,∀j∈J.
其中，目标函数（1）旨在最大化“被保护”的生物数量，其中“被保护”指被以不低于 α i \alpha_i αi的可靠性保护；约束条件（2）表示自然保护区的总面积不得超过预算上界 T T T；约束条件（3）是本文的一个创新点，表示生物 i i i被集合 N i N_i Ni中区域保护的独立联合概率不小于可靠性阈值 α i \alpha_i αi，该约束也可自动推导出0-1决策变量 Y i Y_i Yi的取值，也表征了决策者的风险厌恶（Risk aversion）程度，若 ∏ j ∈ N i ( 1 − P i j ) X j ≤ ( 1 − α i ) \prod\limits_{j\in N_i}(1-P_{ij})^{X_j}\leq(1-\alpha_i) j∈Ni∏(1−Pij)Xj≤(1−αi)，且考虑到最大化的目标， Y i Y_i Yi应取值为1；若 ∏ j ∈ N i ( 1 − P i j ) X j > ( 1 − α i ) \prod\limits_{j\in N_i}(1-P_{ij})^{X_j}>(1-\alpha_i) j∈Ni∏(1−Pij)Xj>(1−αi)，则 Y i Y_i Yi应取值为0，表示生物 i i i无法按期望的可靠性被保护；约束条件（4）是（3）的扩展，其中 M M M表示一些需要被重点保护的生物，其可靠性阈值是一个更为严格的数值 β i \beta_i βi；约束（5）表示了两个0-1决策变量。
初步分析这一模型，这是一个非线性0-1整数规划问题，其中，约束条件（3）和（4）引入了非线性。为了使得模型可以被高效地用求解器求解并分析最优性，本文利用了这两个约束条件良好的结构，引入log算子进行模型线性化。
3. 模型线性化
约束条件（3）的构造相对巧妙，具备良好的结构，通过两边同时取log变换进行线性化
∑
j
∈
N
i
X
j
ln
(
1
−
P
i
j
)
≤
Y
i
ln
(
1
−
α
i
)
,
∀
i
∈
I
.
\begin{equation} \sum\limits_{j\in N_i}X_j\ln(1-P_{ij})\leq Y_i\ln(1-\alpha_i), \forall i\in I. \end{equation}
j∈Ni∑Xjln(1−Pij)≤Yiln(1−αi),∀i∈I.注意到ln里的数值均为[0, 1]的概率值，因而ln项的值始终为负值，我们可以在等式两边同时乘以-1，并得到
Y
i
≤
∑
J
∈
N
i
X
j
ln
(
1
−
P
i
j
)
ln
(
1
−
α
i
)
,
∀
i
∈
I
.
\begin{equation} Y_i\leq\frac{\sum\limits_{J\in N_i}X_j\ln(1-P_{ij})}{\ln(1-\alpha_i)}, \forall i\in I. \end{equation}
Yi≤ln(1−αi)J∈Ni∑Xjln(1−Pij),∀i∈I.
同理，可以对约束（4）进行线性化。通过移项、等式两边乘以-1、取log变换，可以得到
∑
j
∈
N
i
X
j
ln
(
1
−
P
i
j
)
≤
ln
(
1
−
β
i
)
,
∀
i
∈
M
.
\begin{equation} \sum\limits_{j\in N_i}X_j\ln(1-P_{ij})\leq \ln(1-\beta_i), \forall i\in M. \end{equation}
j∈Ni∑Xjln(1−Pij)≤ln(1−βi),∀i∈M.
通过将原优化问题中的约束条件（3）和（4）替换为式（6）和（8），原优化问题即可被转换为线性0-1整数规划问题。如果没有上述线性化过程，我们要处理一个繁琐的非线性整数规划模型，并应用一些无法得到最优性保证的启发式算法求解。
4. 实验设定、优化求解与决策分析
4.1 实验设定
本文基于苏必利尔国家森林（Superior National Forest）进行的数据进行实验，研究如何为其选址科研自然保护区（Research natural areas, RNAs）。如图2左图所示，苏必利尔国家森林公园位于美国与加拿大的边境地区（黑色区域）；如图2右图所示，黑色区域表示备选区域，共33个，带有字母数字标签的阴影区域表示5个亚组，包含125种待研究与保护的生物群落。因而生物出现-不出现（Presence-absence）在备选区域的概率数据矩阵尺度为33×125=4,125。
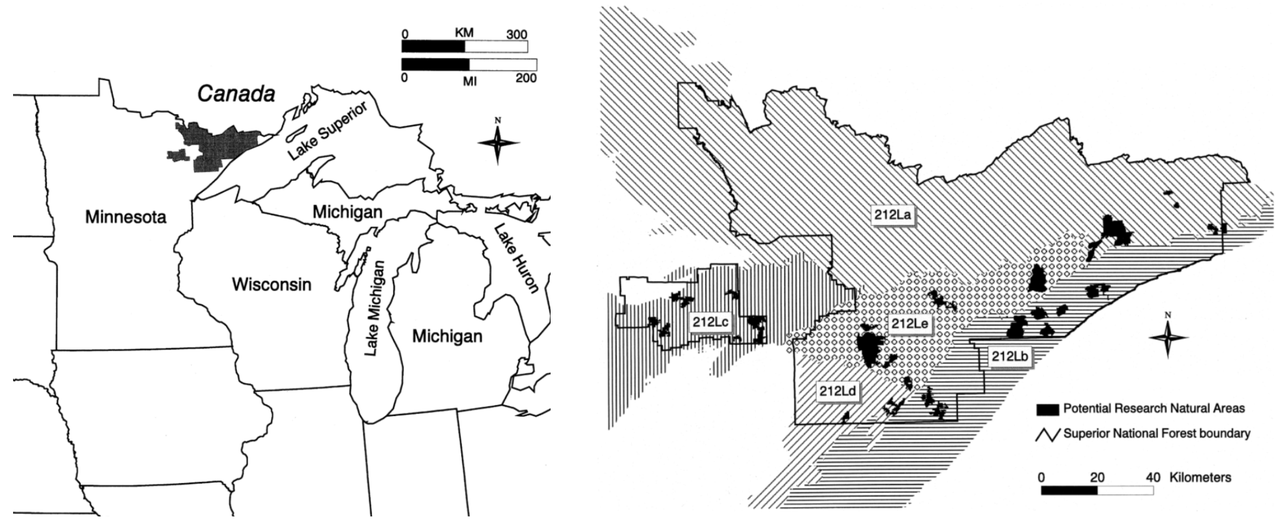
图2 苏必利尔国家森林公园（Superior National Forest）
4.2 优化求解
针对模型线性化后得到的线性0-1整数规划模型，本文在IBM300PL计算机上调用GAMS/OSL 2.25（GAMS Development Corporation 1990, Optimization Subroutine Library, FORTRAN-based）求解，内置算法框架为分支定界法**（Branch-and-bound, B&B）**，其中，线性规划松弛问题由原始-对偶预测-校正障碍内点法（Primal-Dual Predictor-Corrector Barrier Interior point algorithm）求解。
4.3 决策分析
对于选址决策者来说，定量优化模型可以助力精准决策，提供更具象的权衡分析（Trade-Off Analysis）。通过所构建的数学模型与优化求解结果，本文提供了四个权衡分析视角，并用三张曲线图直观显示。
视角一（图3）：自然保护区总面积与保护生物群落数的权衡。随着自然保护区总面积的减少，所能可靠地保护的生物群落数减少，这也是符合常识的。权衡分析曲线可以进一步量化常识，同时，拐点C也可以辅助决策者给出最为经济的生态保护方案。此外，研究人员发现，由于许多生物群落可能出现在多个备选区域，有可能在不减少所能保护生物群落数的前提下，进一步优化总面积，即点A到点B。
视角二（图3）：考虑不同可靠性的自然保护区总面积与保护生物群落数的权衡。考虑拐点C、E，虽然两者对应的总面积一致，但由于拐点E所在曲线的可靠性阈值由100%下降为95%，这种**“宽容度**”，也即较好的**风险厌恶（Risk aversion）**程度使得理论上所能保护的生物群落数更多。
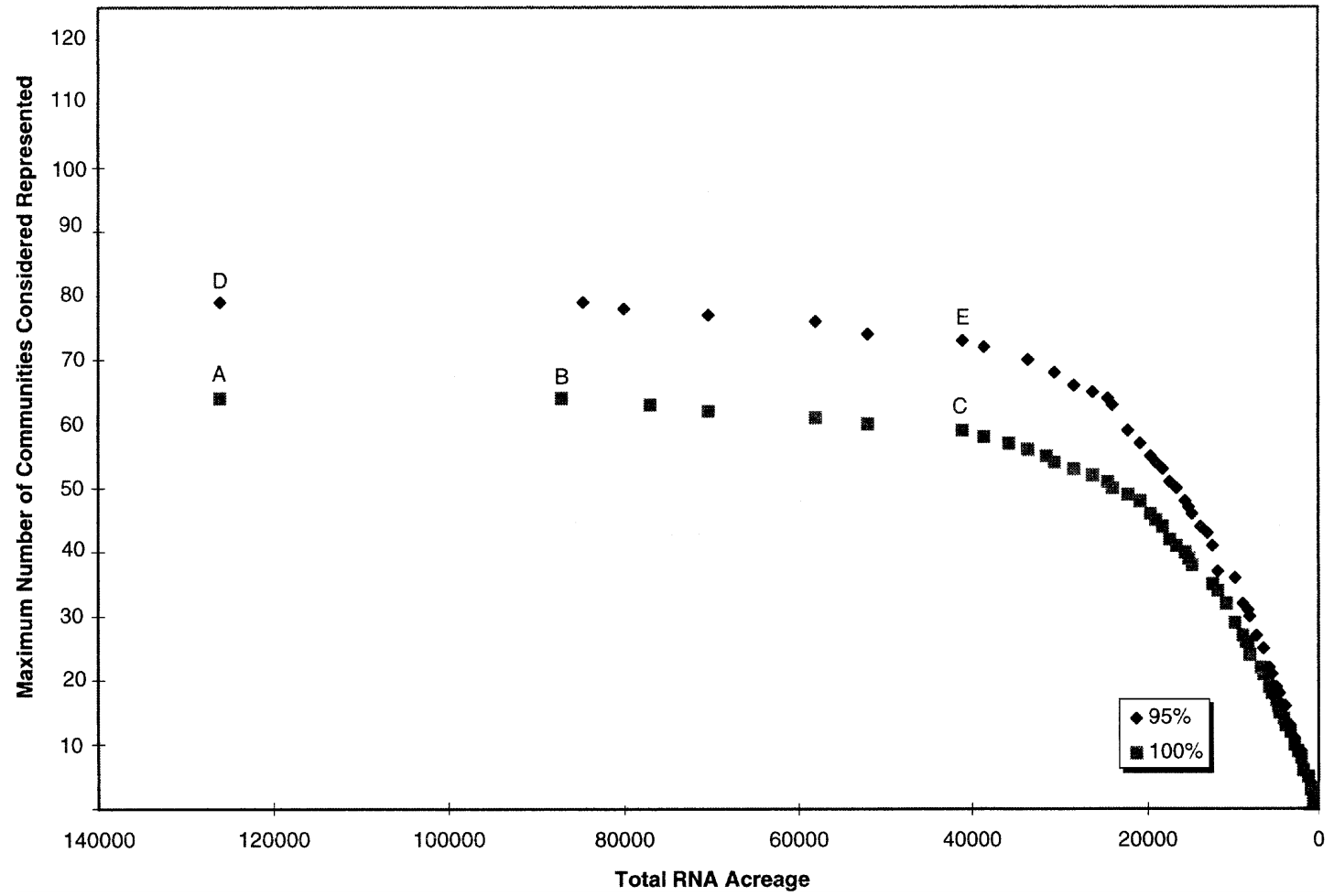图3 考虑不同可靠性的自然保护区总面积与保护生物群落数的权衡
视角三（图4）：不同可靠性阈值与保护生物群落数的权衡。是随着可靠性阈值的不断降低，即决策者态度的不断“宽容”，理论上所能保护的生物群落数更多。另一个现象是曲线上升过程中表现的边际收益（Marginal gains），即前期随着可靠性阈值从100%降低为95%，所能保护的生物群落数增长许多。这可能是由于许多生物群落的对应数值仅在阈值95%下少许造成的。决策者应当注意这一现象并充分把握边际收益，决策出最高效的保护方案。
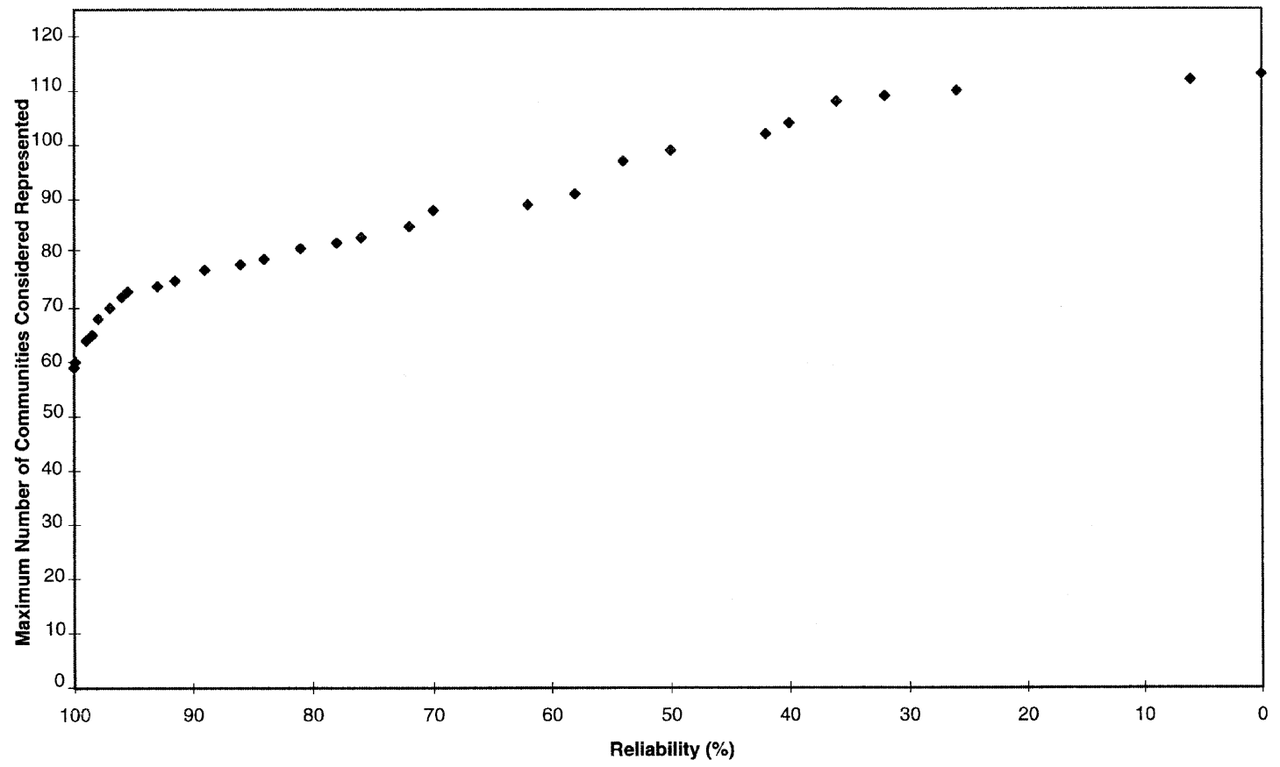
图4 不同可靠性阈值与保护生物群落数的权衡
视角四（图5）：自然保护区总面积与保护生物群落数的权衡，但考虑需要被重点保护的生物群落。根据图5所示，“80% w/o”表示可靠性阈值为80%但没有重点保护的考虑，“80% w/”表示其中有5个生物群落的保护可靠性阈值为95%。可以看出，两条曲线在前期的走势相近，而随着总面积的减小，在后期出现了分叉，考虑重点保护的一条曲线整体略低于未考虑重点保护的。
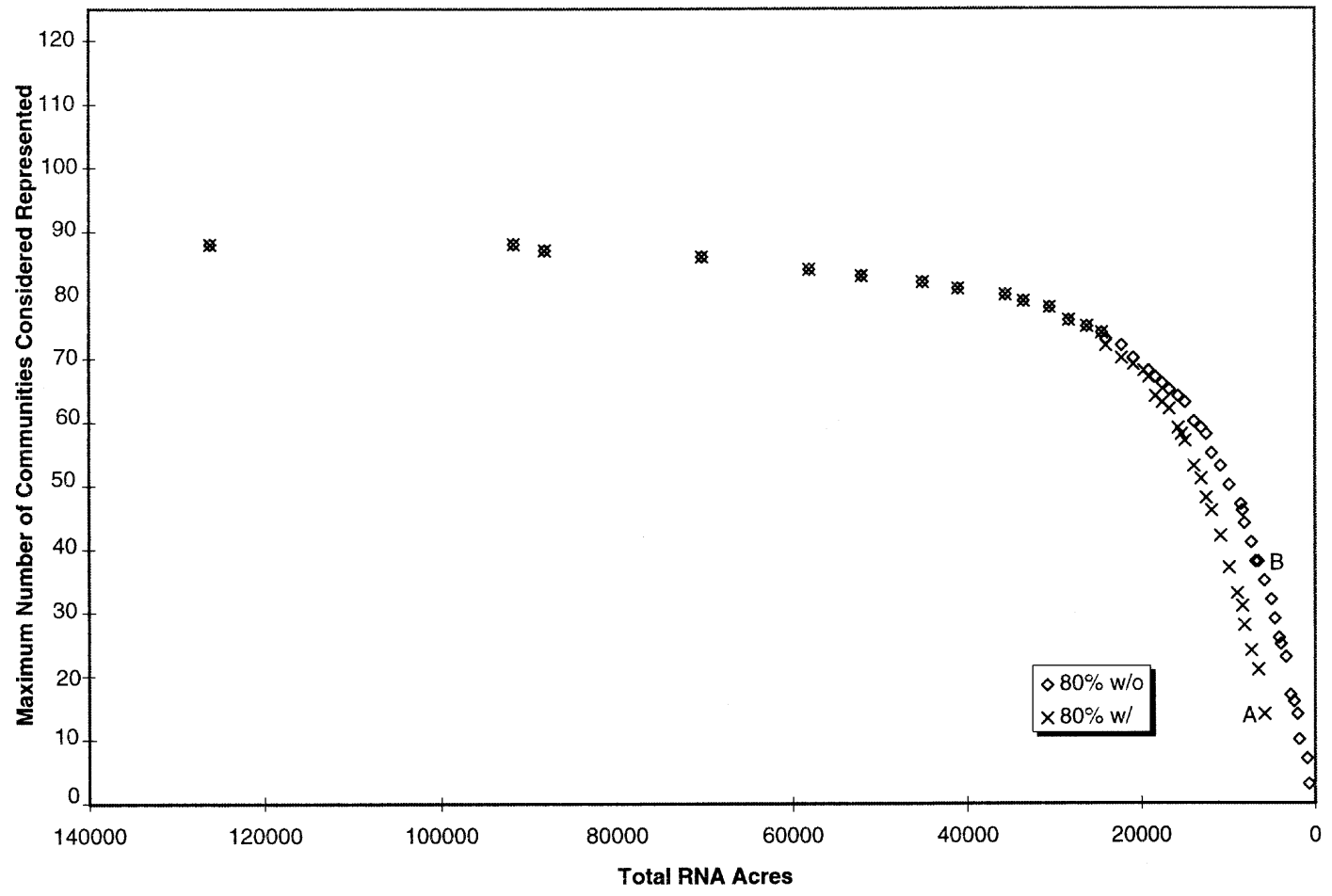
图5 自然保护区总面积与保护生物群落数的权衡，但考虑需要被重点保护的生物群落
5. 总结与讨论
本文针对自然保护区选址这一颇具实际意义的问题，考虑决策中的不确定性与概率数据，设计了非线性0-1整数规划模型COMPRES并进行了模型线性化。通过优化求解这一数学模型，本文为决策者提供了定量研究工具与权衡分析手段。
本文讨论了一些潜在的研究方向。首先，本文求解的案例尚属中小规模，面对潜在的大规模问题场景，我们应定制更高效的求解算法（例如分支定价定切算法、启发式算法等）。其次，概率数据的精准度量与估计是一个值得研究的问题。高质量的输入也有助于输出精准决策结果。输入的概率数据往往需要通过专家评估、打分来确定。专家通过全面考量航空摄影图片、土壤类型、水分状况、实地考察数据等多源信息，给出概率数据的数值。本文作者与美国森林署（U.S. Forest Service）的专家进行沟通讨论。最后，本文提出的COMPRES模型不仅可以应用于自然保护区选址问题，还可以扩展应用于类似的不确定性选址问题，例如警察局的选址（区域犯罪事件频次不确定）或对空监测雷达站的部署（雷达信号对空中目标探测的概率性）等。
保护好生态环境，我们需要拿出更多智慧。让我们用所学的运筹优化知识，更好地回答“神奇动物在哪里”的环境保护之问吧！
参考文献：
[1] Robert G. Haight, Charles S. Revelle, Stephanie A. Snyder, (2000) An Integer Optimization Approach to a Probabilistic Reserve Site Selection Problem. Operations Research 48(5):697-708. https://doi.org/10.1287/opre.48.5.697.12411
[2] Dobson, A. P., Rodriguez, J. P., Roberts, W. M., & Wilcove, D. S. (1997). Geographic distribution of endangered species in the United States. Science, 275(5299), 550-553.
[3] Toregas, C., Swain, R., ReVelle, C., & Bergman, L. (1971). The location of emergency service facilities. Operations Research, 19(6), 1363-1373.
[4] Church, R., & ReVelle, C. (1974, December). The maximal covering location problem. In Papers of the regional science association (Vol. 32, No. 1, pp. 101-118). Berlin/Heidelberg: Springer-Verlag.
