【力扣】从零开始的动态规划
文章目录
- 【力扣】从零开始的动态规划
- 开头
- 139. 单词拆分
- 解题思路
- 45. 跳跃游戏 II
- 解题思路
- 5. 最长回文子串
- 解题思路
- 1143. 最长公共子序列
- 解题思路
- 931. 下降路径最小和
- 解题思路
开头
本力扣题解用5题来引出动态规划的解题步骤,用于本人进阶掌握动态规划,在刷题过程中写下的一些解题步骤与思路,供大家一起学习
139. 单词拆分
139. 单词拆分
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
**注意:**不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
解题思路
状态表示: dp[i]表示字符串以0到i-1的字符串,能否组成字串
初始状态:dp[0]=true,没有字符串的情况肯定为true,如果这个为false,那么后面全部为false
状态转移方程:
可以把一个字符串来看成两段,0~j-1和j~i,前面一半可以看成dp[j],因为看下状态表示就知道了,dp[i]表示字符串以0到i-1的字符串, 带入j得dp[j]表示字符串以0到j-1的字符串。
后一半直接在哈希表中找子串是否存在,找到了就是true,如果两个字串同时为true,那么dp[i]=true
因为以0~i的字符串的分解的情况有很多种,只要其中一种为true,那么就是true,直接break;
所以动态转移方程为:
if(dp[j] && set.contains(s.substring(j,i)))
{
dp[i]=true;
break;
}
import java.util.HashSet;
import java.util.Set;
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
Set<String> set=new HashSet<>(wordDict);
int n=s.length();
boolean[] dp=new boolean[n+1];
dp[0]=true;
//从第i个字符结束的
for(int i=0;i<=n;i++)
{
for(int j=0;j<i;j++)
{
if(dp[j] && set.contains(s.substring(j,i)))
{
dp[i]=true;
break;
}
}
}
return dp[n];
}
}
45. 跳跃游戏 II
45. 跳跃游戏 II
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
解题思路
状态表示: dp[i]表示从1开始跳到第i个数的最小次数
**初始状态:**第1个元素是起点,可以到达,其他所有结点默认无法到达,设置一个很大的初始值
状态转移方程:
第i个数可以从前面任意一个跳跃距离大于两个结点距离的结点,及判断条件if(nums[j]>=i-j),在这些满足要求的结点中取最小值,方程为
dp[i]=min(dp[0],dp[1],dp[2]...dp[n-1])+1,写成循环结构,最终方程为:dp[i]=Math.min(dp[i],dp[j]+1);
import java.util.Arrays;
class Solution {
public int jump(int[] nums) {
int n=nums.length;
int[] dp=new int[n];
Arrays.fill(dp,Integer.MAX_VALUE);
//状态表示:前跳到第i个的最小次数
dp[0]=0;
for(int i=1;i<n;i++)
{
for(int j=0;j<i;j++)
{
int l=i-j;
if(nums[j]>=l)
{
dp[i]=Math.min(dp[i],dp[j]+1);
}
}
}
return dp[n-1];
}
}
5. 最长回文子串
5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
解题思路
状态表示: dp[i][j] 表示 i到j是否是一个回文串
**初始状态:**无
状态转移方程:
想要知道dp[i][j]是否是一个回文子串,只需知道dp[i+1][j-1]是否是一个回文子串并且外层的字符相等即s[i]==s[j],那么dp[i][j]就是一个回文子串,还有一种特殊情况是:要判断的字符串只有两个字符时,不用再判断dp[i+1][j-1]是否是一个回文子串,只需判断这两个字符是否相等即可
**循环顺序:**想要知道循环顺序是从大到小,还是从小到大,我们要知道dp数组中哪个要先算出来 ,哪个后算出来,比如想要知道dp[i][j]是否是一个回文子串,就得先知道dp[i+1][j-1]是否也是一个回文子串,所以dp[i+1][j-1]要被先计算出来,分为两重循环来分析
外重循环i+1比i要先知道,所以,i从大到小循环
内重循环j-1比j要先知道,所以j从小到大循环
又因为j一定要大于等于i,因为范围表示是i~j,所以j从i到n-1
if(s.charAt(i)==s.charAt(j))
{
if(j-i<2 || dp[i+1][j-1] )
dp[i][j]=true;
}
class Solution {
public String longestPalindrome(String s) {
int n=s.length();
//状态表示:i到j是否是一个回文串
boolean[][] dp=new boolean[n][n];
//dp[i][j]=dp[i+1][j-1] && s.charAt(i)==s.charAt(j)
String str="";
for(int i=n-1;i>=0;i--)
{
for(int j=i;j<n;j++)
{
if(s.charAt(i)==s.charAt(j))
{
if(j-i<2 || dp[i+1][j-1] )
dp[i][j]=true;
}
if(dp[i][j] && (j-i+1)>str.length())
{
str=s.substring(i,j+1);
}
}
}
return str;
}
}
1143. 最长公共子序列
1143. 最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"是"abcde"的子序列,但"aec"不是"abcde"的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
解题思路
状态表示:dp[i][j] 表示 text1[0:i-1] 和 text2[0:j-1] 的最长公共子序列
**状态转移方程:**知道状态定义之后,我们开始写状态转移方程。
当 text1[i - 1] == text2[j - 1] 时,说明两个子字符串的最后一位相等,所以最长公共子序列又增加了 1,所以 dp[i][j] = dp[i - 1][j - 1] + 1;举个例子,比如对于 ac 和 bc 而言,他们的最长公共子序列的长度等于 a 和 b 的最长公共子序列长度 0 + 1 = 1。
当 text1[i - 1] != text2[j - 1] 时,说明两个子字符串的最后一位不相等,那么此时的状态 dp[i][j] 应该是 dp[i - 1][j] 和 dp[i][j - 1] 的最大值。举个例子,比如对于 ac和 bc 而言,他们的最长公共子序列的长度等于 ① ace 和 b 的最长公共子序列长度0 与 ② ac 和 bc 的最长公共子序列长度1 的最大值,即 1。
所以状态转移方程为:当text[i-1]==text[j-1]时.dp[i][j]=dp[i-1][j-1]+1
当text[i-1]!=text[j-1]时,dp[i][j]=max(dp[i−1][j],dp[i][j−1])
**初始值:**初始化就是要看当 i = 0 与 j = 0 时, dp[i][j] 应该取值为多少。
当 i = 0 时,dp[0][j] 表示的是 text1 中取空字符串 跟 text2 的最长公共子序列,结果肯定为 0.
当 j = 0 时,dp[i][0] 表示的是 text2 中取空字符串 跟 text1 的最长公共子序列,结果肯定为 0.
综上,当 i = 0 或者 j = 0 时,dp[i][j] 初始化为 0.
遍历方向与范围:由于 dp[i][j] 依赖与 dp[i - 1][j - 1] , dp[i - 1][j], dp[i][j - 1],所以 iii 和 jjj 的遍历顺序肯定是从小到大的。 另外,由于当 i 和 j 取值为 0 的时候,dp[i][j] = 0,而 dp 数组本身初始化就是为 0,所以,直接让 i 和 j 从 1 开始遍历。遍历的结束应该是字符串的长度为 len(text1) 和 len(text2)
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int n=text1.length();
int m=text2.length();
int[][] dp=new int[n+1][m+1];
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(text1.charAt(i-1)==text2.charAt(j-1))
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
}
}
return dp[n][m];
}
}
931. 下降路径最小和
931. 下降路径最小和
给你一个 n x n 的 方形 整数数组 matrix ,请你找出并返回通过 matrix 的下降路径 的 最小和 。
下降路径 可以从第一行中的任何元素开始,并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列(即位于正下方或者沿对角线向左或者向右的第一个元素)。具体来说,位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。
示例 1:
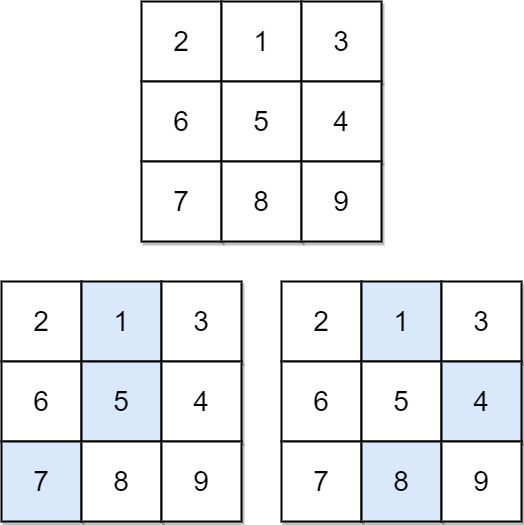
输入:matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出:13
解释:如图所示,为和最小的两条下降路径
解题思路
状态表示:dp[i][j]表示走到matrix[i][j]的最小下降和
**初始值:**第一行全是0,因为在原地(起点)
**状态转移方程:**到达dp[i][j]可以从上一层的相邻元素到达,取其中的最小值并加上一步的数量,即dp[i][j]=min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])+matrix[i][j],因为要判断边界条件,在最左边和最右边只能从上一层的两个到达。
综上所诉,状态转移方程为:
if(j==0)
dp[i][j]=Math.min(dp[i-1][j],dp[i-1][j+1])+matrix[i][j];
else if(j==m-1)
dp[i][j]=Math.min(dp[i-1][j-1],dp[i-1][j])+matrix[i][j];
else
dp[i][j]=Math.min(dp[i-1][j-1],Math.min(dp[i-1][j],dp[i-1][j+1]))+matrix[i][j];
**答案:**根据题目要求,到达最后一行的最少下降和,再看状态表示:dp[i][j]表示走到matrix[i][j]的最小下降和,所以答案就在dp的最后一行中,取最后一行的最小值即是答案
class Solution {
public int minFallingPathSum(int[][] matrix) {
int n=matrix.length;
int m=matrix[0].length;
int[][] dp=new int[n][m];
for(int j=0;j<m;j++)
{
dp[0][j]=matrix[0][j];
}
for(int i=1;i<n;i++)
{
for(int j=0;j<m;j++)
{
if(j==0)
dp[i][j]=Math.min(dp[i-1][j],dp[i-1][j+1])+matrix[i][j];
else if(j==m-1)
dp[i][j]=Math.min(dp[i-1][j-1],dp[i-1][j])+matrix[i][j];
else
dp[i][j]=Math.min(dp[i-1][j-1],Math.min(dp[i-1][j],dp[i-1][j+1]))+matrix[i][j];
}
}
int min=Integer.MAX_VALUE;
for(int j=0;j<m;j++)
{
min=Math.min(min,dp[n-1][j]);
}
return min;
}
}